Навигация
Инверсия плоскости в комплексно сопряженных координатах
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Вятский государственный гуманитарный университет
Математический факультет
Кафедра алгебры и геометрии
Выпускная квалификационная работа
Инверсия плоскости
в комплексно сопряженных координатах
Выполнила: студентка V курса
математического факультета
Дмитриенко Надежда Александровна
Научный руководитель:
старший преподаватель кафедры
алгебры и геометрии
Александр Николаевич Суворов
Рецензент:
Допущена к защите в государственной аттестационной комиссии
«___»__________2005 г. Зав. кафедрой В.М. Вечтомов
«___»___________2005 г. Декан факультета В.И. Варанкина
Киров
2005
Содержание
Введение........................................................................................................... 3
Глава 1. Основные положения теории инверсии........................................... 4
1.1. Общие сведения о комплексной плоскости......................................... 4
1.2. Определение инверсии – симметрии относительно окружности........ 5
1.3. Формула инверсии в комплексно сопряженных координатах......... 11
1.4. Неподвижные точки и окружность инверсии.................................... 11
1.5. Образы прямых и окружностей при обобщенной инверсии............ 12
1.6. Свойства обобщенной инверсии........................................................ 19
Глава 2. Применение инверсии при решении задач
и доказательстве теорем................................................................. 30
2.1. Применение инверсии при решении задач на построение............... 30
2.2. Применение инверсии при доказательстве........................................ 41
Заключение.................................................................................................... 43
Библиографический список........................................................................... 44
Введение
В наш век современных технологий так и хочется привлечь компьютер для решения задач, в частности, геометрических. Было бы замечательно, если бы от пользователя требовалось только занести в программу нужные данные, а последняя сама бы все рассчитала и выдала, к примеру, радиус и центр искомой окружности. Но вся проблема в том, что программа может работать только с координатами. И есть смысл перевода наиболее эффективных с точки зрения решения задач преобразований, в число которых входит и инверсия, на язык координат. Наиболее просто это получается на комплексной плоскости. Изучению преобразования инверсии комплексной плоскости и посвящена эта дипломная работа.
Цель работы состоит в следующем: обобщить и систематизировать основные факты об инверсии комплексной плоскости и показать применение этого преобразования при решении задач и доказательстве теорем.
Поставленная цель предполагала решение следующих задач:
· вывод комплексной формулы инверсии;
· доказательство основных свойств инверсии на комплексной плоскости;
· решение нескольких задач при помощи инверсии комплексной плоскости;
· доказательство ряда теорем при помощи инверсии комплексной плоскости.
Оказалось, что не так много специальных работ по теме. Инверсия комплексной плоскости оказалась крайне слабо освещена в литературе по сравнению с инверсией евклидовой плоскости. Поступали следующим образом: брали известный факт из евклидовой плоскости, а потом доказывали его методом комплексно сопряженных координат. Чаще всего такие доказательства были понятнее и короче, чем исходные.
Глава 1
Основные положения теории инверсии
1.1. Общие сведения о комплексной плоскости. Зададим на плоскости прямоугольную декартову систему координат 0xy. Тогда каждому комплексному числу z, представленному в алгебраической форме ![]() , можно однозначно поставить в соответствие точку М плоскости с координатами
, можно однозначно поставить в соответствие точку М плоскости с координатами ![]() . Комплексное число z называют комплексной координатой соответствующей точки М и пишут:
. Комплексное число z называют комплексной координатой соответствующей точки М и пишут: ![]() .
.
Следовательно, множество точек евклидовой плоскости находится во взаимно однозначном соответствии с множеством комплексных чисел. Эту плоскость называют плоскостью комплексных чисел.
Все необходимые сведения об этой плоскости очень хорошо даны в книге Я. П. Понарина [3]. Здесь приведем лишь некоторые формулы, взятые из того же источника, использованные в работе.
Расстояние между двумя точками с координатами а и b равно ![]() .
.
Уравнение прямой в канонической форме: ![]() ,
, ![]() .
.
Уравнение окружности с центром в точке s и радиусом r: ![]() . Также часто используют запись
. Также часто используют запись ![]() ,
, ![]() ,
, ![]() , где центр
, где центр ![]() , радиус
, радиус ![]() .
.
Скалярное произведение векторов: ![]() .
.
Коллинеарность трех точек с координатами а, b и с: ![]() .
.
Критерий коллинеарности векторов: ![]() .
.
Расстояние от точки с координатой z0 до прямой ![]() ,
, ![]() :
: 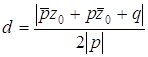 .
.
Критерий параллельности двух прямых ![]() и
и ![]() , заданных в канонической форме:
, заданных в канонической форме: 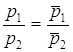 .
.
Критерий перпендикулярности двух прямых ![]() и
и ![]() , заданных в канонической форме:
, заданных в канонической форме: 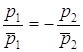 .
.
Двойное отношение четырех точек плоскости с координатами а, b, с и d: ![]() ; аргумент w равен ориентированному углу между окружностями abc и abd.
; аргумент w равен ориентированному углу между окружностями abc и abd.
Критерий принадлежности четырех точек одной окружности или прямой: ![]() .
.
Критерий ортогональности окружностей ![]() ,
, ![]() и
и ![]() ,
, ![]() :
: ![]() .
.
Параллельный перенос на вектор с координатой r: ![]() .
.
Гомотетия с центром s и коэффициентом s: ![]() ,
, ![]() .
.
Осевая симметрия с осью симметрии ![]() , где
, где ![]() :
: ![]() .
.
Центральная симметрия с центром ![]() :
: ![]() .
.
Похожие работы
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
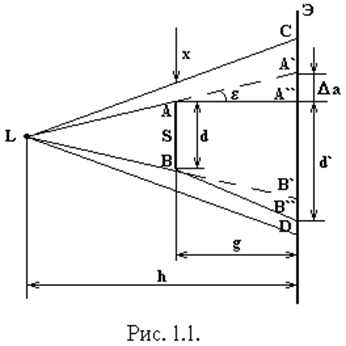
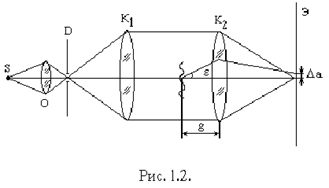
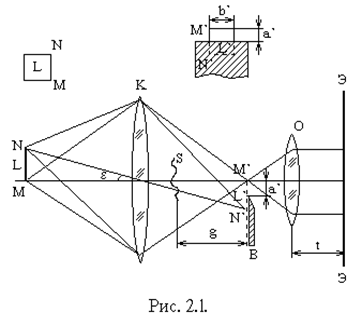
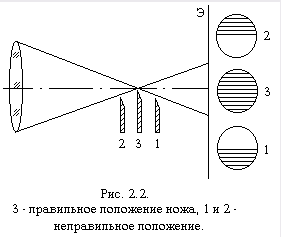
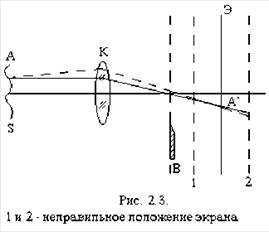
... неоднородность имеет значительную глубину. Прибор интерференционно-теневой ИАБ-458 Прибор интерференционно-теневой ИАБ-458 предназначен для качественных и количественных исследований теневым методом неоднородностей оптически прозрачных сред. В приборе реализуются следующие методы исследования: светящейся точки, щели и ножа, щели и нити, сдвиговой интерферометрии и голографии. На рис. 2.4 ...
... , имеющие электрический заряд Q = -1 и Q = 1 соответственно. Также являются стабильными частицами нейтрино и антинейтрино, т.к. это самые легкие носители лептонных зарядов Le, , . 3. СВЯЗЬ ЗАКОНОВ СОХРАНЕНИЯ С СИММЕТРИЕЙ СИСТЕМЫ Одним из важных открытий современного естествознания является тот факт, что все многообразие окружающего нас физического мира связано с тем или иным ...
... и в тех, когда физическое качество переходит в химическое, химическое в биологическое, биологическое в надбиологическое, профанное в сакральное и наоборот, - мы неизменно имеем дело с синергетикой, с феноменологией сопряжении и метаморфоз, с ситуацией взаимопревращений противоположностей, с теми неаддитивно-мета-системными переходами, которые в конкретно-образной (мифологической, поэтической) или ...


0 комментариев