Логические функции можно задавать различными способами: словесно, таблицей истинности, аналитическим выражением, используя условные графические обозначения. В каждом конкретном случае используется наиболее удобный способ.
Базовым способом для задания логической функций является таблица истинности. В таблице истинности заданы все возможные комбинации значений переменных и соответствующие им значения функций.
Таблица истинности включает в себя один столбец с номерами строк (он не обязателен и может отсутствовать), столбцы с переменными, (их количество равно количеству переменных), Столбцы с функциями (их количество равно числу выходов логической функции). Полная таблица истинности содержит 2n строк, где n число переменных. Строки в таблице истинности нумеруются, начиная с нуля.
Комбинации переменных в таблице истинности можно размещать в произвольном порядке, но лучше придерживаться следующей системы. Старшая переменная должна обозначаться большим индексом и размещаться в левом крайнем столбце, остальные по мере убывания старшинства. Комбинация значений переменных в строке должна выражать в двоичном коде номер строки. Строки в таблице размещаются в монотонно возрастающем порядке, начиная с нулевой. Такие правила обеспечивают безошибочное заполнение таблицы истинности и облегчают работу с ней. Таблица истинности произвольной функции для трех переменных, заполненная по этим правилам, представлена на рисунке 1.1.
|
Номер строки |
Переменные |
Функция |
||
|
Х 3 |
Х 2 |
Х 1 |
f (ν) |
|
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
0 |
1 |
0 |
1 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
0 |
Таблица истинности для трех переменных
Из представленной таблицы следует простой, быстрый и безошибочный способ ее заполнения значениями переменных: в первом столбце переменные чередуются через раз (0-1-0-1 и т.д.), во втором столбце чередуются через два раза (00-11-00 и т. д.), в третьем столбце через четыре раза (0000-1111-0000 и т. д.), в четвертом будут чередоваться через восемь раз и т. д. Степень чередования для следующей старшей переменной удваивается.
При словесном описании функции принято формулировать, в каких случаях функция равна 1.
Похожие материалы
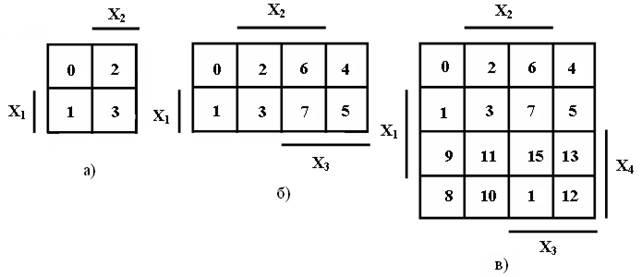
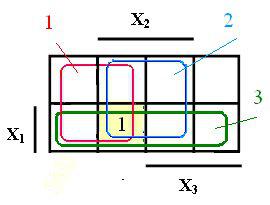
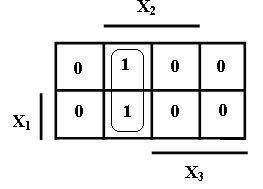
... на рисунке 1 для двух переменных а), трех переменных б) и четырех переменных в). Принципиального значения не имеет, каким вариантом изображения карты Карно пользоваться. В дальнейшем для минимизации используются карты Карно, представленные на рисунке 1 и студентам рекомендуется тоже их использовать. В картах Карно, показанных на рисунке 1, области, где переменные находятся без инверсий (X i), ...
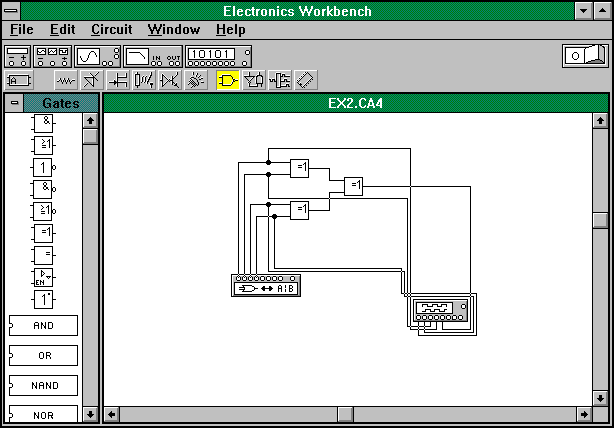
... И-НЕ. Для выполнения этой операции (при имеющемся в окошке булевом выражении) следует “нажать” стрелкой кнопку: 3. Математические модели и эквивалентные схемы в программе логического проектирования Любой реальный логический элемент(ЛЭ) не мгновенно реагирует на изменения входных сигналов, поэтому имеется некоторая паразитная задержка между моментом времени, в который на его входы поступают новые ...
... в виде конъюнкции простых дизъюнкций, то такая форма представления называется конъюнктивной нормальной формой (КНФ). Например: Любая логическая функция может иметь несколько представлений в виде днф и кнф. Форма представления функции в виде дизъюнкции минтермов называется совершенной дизъюнктивной нормальной формой (СДНФ). Например: Форма представления функции в ...
0 комментариев