Аналитическое выражение логической функции, составленное в СДНФ или СКНФ по таблице истинности, как правило, является избыточным. В большинстве случаев его можно упростить. Т. е. найти такое аналитическое выражение, которое эквивалентно исходному выражению функции, но содержит меньшее число переменных и (или) операций. Процедура уменьшения числа переменных и (или) операций в аналитическом выражении логической функции называется минимизацией.
Практическая цель минимизации является уменьшение числа логических элементов при аппаратной реализации логической функции, и, как следствие этого, повышение быстродействия, уменьшение размеров, стоимости и потребления энергии у проектируемой логической схемы.
Минимизацию можно проводить различными методами. При числе переменных шесть и меньше наибольшее распространение имеет метод с использованием карты Карно (диаграммы Вейча).
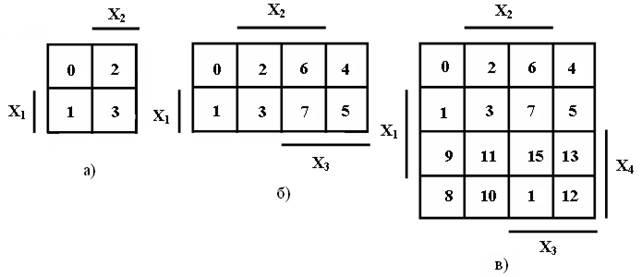
Рисунок 1
Карта Карно представляет собой составленную по определенным правилам таблицу, куда занесены все значения логической функции. Таким образом, карта Карно является одним из способов задания логических функций. Вариантов изображения карты Карно много. Один из вариантов показан на рисунке 1 для двух переменных а), трех переменных б) и четырех переменных в). Принципиального значения не имеет, каким вариантом изображения карты Карно пользоваться. В дальнейшем для минимизации используются карты Карно, представленные на рисунке 1 и студентам рекомендуется тоже их использовать.
В картах Карно, показанных на рисунке 1, области, где переменные находятся без инверсий (X i), обозначены чертой. В областях, не обозначенных чертой, переменные находятся с инверсий (![]() ). Например, к области переменных Х 3 относятся клетки 4,5,6,7,12,13,14,15, а к области
). Например, к области переменных Х 3 относятся клетки 4,5,6,7,12,13,14,15, а к области ![]() относятся клетки 0,1,4,5,8,9,12,13. Таким образом, в картах Карно, показанных на рисунке 1 имеются области переменных
относятся клетки 0,1,4,5,8,9,12,13. Таким образом, в картах Карно, показанных на рисунке 1 имеются области переменных ![]() Младшая переменная обозначается Х 1, а старшинство остальных переменных линейно возрастает с увеличением индекса.
Младшая переменная обозначается Х 1, а старшинство остальных переменных линейно возрастает с увеличением индекса.
Каждой клетке карты Карно соответствует определенный и единственный минтерм (макстерм). Индекс минтерма является номером клетки карты Карно. Номер клетки также соответствует числу, которое выражает двоичная комбинация значений переменных, находящихся в строке таблицы истинности.
Карта Карно заполняется по таблице истинности или по аналитическому выражению функции, которую нужно минимизировать.
Если функция задана таблицей истинности, то порядок заполнения карты Карно следующий.
Берется строка таблицы истинности, и определяются области переменных, в которых находится клетка, соответствующая выбранной строке. Затем на карте Карно эти области выделяются. Искомой будет та клетка, которая одновременно находится во всех выделенных областях переменных (принадлежит одновременно всем выделенным областям, является для них общей). В найденную клетку проставляется значение функции, соответствующее комбинации переменных выбранной строки. Эта процедура повторяется для всех строк таблицы истинности до полного заполнения карты Карно.
Таблица 1
|
Номер строки |
Переменные |
Функция |
||
|
Х 3 |
Х 2 |
Х 1 |
f (ν) |
|
|
0 |
0 |
0 |
0 |
0 |
|
1 |
0 |
0 |
1 |
1 |
|
2 |
0 |
1 |
0 |
1 |
|
3 |
0 |
1 |
1 |
1 |
|
4 |
1 |
0 |
0 |
0 |
|
5 |
1 |
0 |
1 |
0 |
|
6 |
1 |
1 |
0 |
1 |
|
7 |
1 |
1 |
1 |
0 |
Пусть, например, требуется в карте Карно найти клетку, соответствующую строке 3 таблицы истинности 1. В этой строке находятся следующие значения переменных: Х3 = 0, Х2 = 1 Х1 =1. На карте Карно (рисунок 2) выделяются области ![]() (инверсное значение потому, что Х3 = 0) - красным цветом (область 1), Х2 - синим цветом (область 2), Х1 - зелёным цветом (область 3). Общей клеткой для всех трех областей будет клетка, выделенная желтым цветом. В эту клетку и проставляется значение функции. Для рассматриваемой комбинации переменных оно равно 1.
(инверсное значение потому, что Х3 = 0) - красным цветом (область 1), Х2 - синим цветом (область 2), Х1 - зелёным цветом (область 3). Общей клеткой для всех трех областей будет клетка, выделенная желтым цветом. В эту клетку и проставляется значение функции. Для рассматриваемой комбинации переменных оно равно 1.
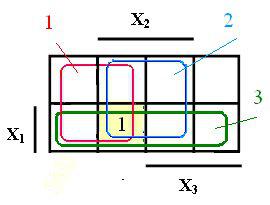
Рисунок 2
Если функция задана аналитическим выражением, то порядок заполнения карты Карно следующий. Сначала функцию приводят к дизъюнктивной нормальной форме, т.е. форме, где инверсии стоят только над отдельными переменными. Это можно сделать, используя теоремы и тождества алгебры логики. Конъюнкции полученного выражения могут содержать от одной переменной до всех используемых в данном случае переменных. Каждая конъюнкция полученного выражения - это конкретная группа клеток карты Карно, в которых должны находиться 1. Такая группа клеток находятся в зоне пересечения областей переменных (одновременно принадлежат областям переменных) входящих в рассматриваемую конъюнкцию. Процедура установки единиц применяется для всех конъюнкций заданного выражения. Если в клетке уже установлена единица при заполнении по предыдущим конъюнкциям, то единица остаётся.
В остальные клетки, где не установлены единицы, устанавливаются нули.
Например, необходимо заполнить карту Карно для выражения ƒ(ν) = ![]() . В это выражение входит сложная конъюнкция
. В это выражение входит сложная конъюнкция ![]() . Применяя для неё правило де Моргана, получим
. Применяя для неё правило де Моргана, получим ![]() =
= ![]() . В дизъюнктивной нормальной форме заданная функция имеет вид ƒ(ν) =
. В дизъюнктивной нормальной форме заданная функция имеет вид ƒ(ν) = ![]() и состоит из трёх конъюнкции. Первая конъюнкция включает в себя одну переменную
и состоит из трёх конъюнкции. Первая конъюнкция включает в себя одну переменную ![]() , значит, единицы устанавливаются в клетках, которые принадлежат области
, значит, единицы устанавливаются в клетках, которые принадлежат области ![]() . Карта Карно для этой конъюнкции с проставленными 1 показана на рисунке 3 а). Вторая конъюнкция включает в себя две переменные:
. Карта Карно для этой конъюнкции с проставленными 1 показана на рисунке 3 а). Вторая конъюнкция включает в себя две переменные: ![]() и
и ![]() , значит, единицы устанавливаются в клетках, которые одновременно принадлежат областям (находятся на пересечении областей)
, значит, единицы устанавливаются в клетках, которые одновременно принадлежат областям (находятся на пересечении областей) ![]() и
и ![]() . Карта Карно для этой конъюнкции с проставленными 1 показана на рисунке 3 б). Третья конъюнкция включает в себя три переменные:
. Карта Карно для этой конъюнкции с проставленными 1 показана на рисунке 3 б). Третья конъюнкция включает в себя три переменные: ![]() ,
, ![]() ,
, ![]() , значит, единицы устанавливаются в клетках, которые одновременно принадлежат областям (находятся на пересечении областей)
, значит, единицы устанавливаются в клетках, которые одновременно принадлежат областям (находятся на пересечении областей) ![]() ,
, ![]() и
и ![]() . Карта Карно для этой конъюнкции с проставленными 1 показана на рисунке 3 в).
. Карта Карно для этой конъюнкции с проставленными 1 показана на рисунке 3 в).
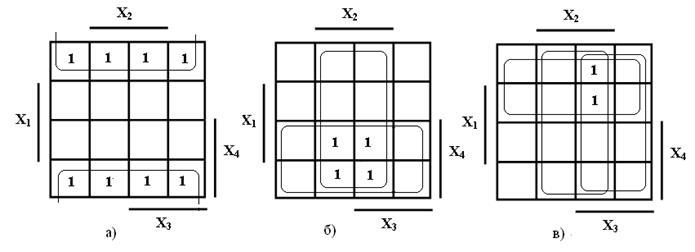
Рисунок 3
При наложении друг на друга всех этих трех карт Карно получится карта, показанная на рисунке 4 а). После проставления 0 в оставшиеся пустые клетки, получится полностью заполненная карта Карно, которая и показана на рисунке 4 б).
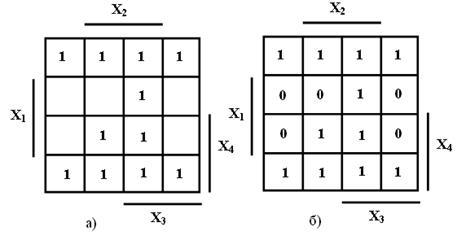
Рисунок 4
После заполнения карты Карно начинается минимизации. В процессе минимизации все клетки, содержащие 1 (либо 0) должны быть объедены в группы.
В группы объединяются соседние клетки, содержащие 1 (либо 0) и образующие прямоугольники или квадрат. Группа должна содержать 2 n клеток (n = 0, 1, 2, 3 и т. д), иными словами 1, 2, 4, 8, 16 и т.д. клеток. Причем нужно стремиться, чтобы групп было как можно меньше, и для достижения этого включать в каждую группу максимально возможное число клеток. Процесс создания групп продолжается до тех пор, пока все клетки не будут объединены в группы. Клетки с 1 (либо 0 ), которые невозможно объединить с другими, образуют группы с числом клеток 1. Одна и та же клетка может входить в несколько групп.
При определении соседних клеток карту Карно можно сворачивать в рулон по горизонтали и по вертикали. В карте Карно на рисунке 1.8в) например, соседними будут клетки 2 и 10; 1, 5, 9 и 13; а также 0, 4, 8 и 12!
Равнозначных вариантов объединения клеток может быть несколько.
Минимизированную функцию записывают в дизъюнктивной нормальной форме (ДНФ) или в конъюнктивной нормальной форме (КНФ). Чаще используется ДНФ. В ДНФ минимизированная функция имеет вид
при объединении клеток с единицами:
![]()
при объединении клеток с нулями:
![]() ,
,
где Сi – конъюнкция для i – ой группы; m – количество групп.
В выражение конъюнкции входят те переменные с инверсией или без инверсии (но не одновременно), в области которых i – ая группа находится вся целиком.
Для определения областей, в которых группа находится целиком, можно предложить следующий алгоритм.
Мысленно или фигурально (например, куском бумаги, вырезанным по размеру области карты Карно) закрывается одна из областей переменных карты Карно. Если рассматриваемая группа клеток карты Карно полностью закрылась и не высовывается из-за закрытой области, значит, данная переменная входит в выражение конъюнкции для рассматриваемой группы клеток. Эта действие повторяется для всех областей карты Карно. Например, у карты Карно четырех переменных это -![]()
Например, необходимо определить, в каких областях переменных полностью находится группа клеток с 1, показанная на рисунке 5.
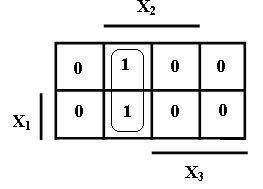
Рисунок 5
Последовательно закрывая области переменных ![]() , получим картину, показанную на рисунке 6.
, получим картину, показанную на рисунке 6.
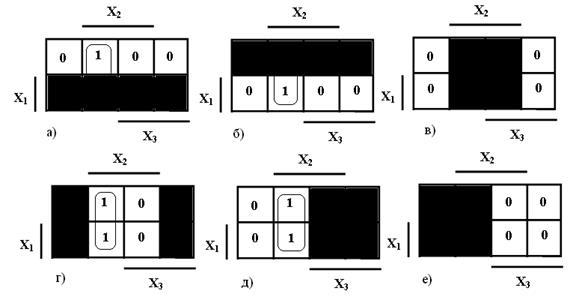
Рисунок 6
Из этого рисунка видно, что группа клеток с 1 полностью закрыта только на рисунках в) и е), на рисунках а) и б) она закрыта только частично, а на рисунках г ) и д) не закрыта вообще. Это значит, что конъюнкция для этой группы клеток будет содержать переменные ![]() , т. е. будет иметь вид
, т. е. будет иметь вид ![]() .
.
Если вырожденная (не для всех переменных определенная) функция задана таблицей истинности, то при заполнении карты Карно в клетки, для которых функция не определена, устанавливают такие значения функции, которые позволяют получить минимальное конечное аналитическое выражение функции. Часто в такие клетки при заполнении карты Карно ставят крестик (Х).
Порядок минимизации функции с помощью карты Карно следующий:
1) Используя таблицу истинности или аналитическое выражение функции, заполняют карту Карно;
2) В карте Карно создаются группы, объединяющие клетки с 1(или с 0). Принципиальной разницы между минимизацией функции по 1 или по 0 нет. Выбирается вариант, при котором функция имеет минимальное выражение;
3) Записывают минимизированное выражение функции в выбранной форме.
Похожие материалы
... X3X4 V X1X2X4 V X1X2X4. Дальнейшее преобразование невозможно. Полученную функцию можно немного упростить с помощью вынесения за скобки общих переменных. 1.3.2 Метод Квайна При минимизации по методу Квайна предполагается, что минимизируемая логическая функция задана в виде ДСНФ. Здесь используется закон неполного склеивания. Минимизация проводится в два этапа: нахождение простых импликант, ...
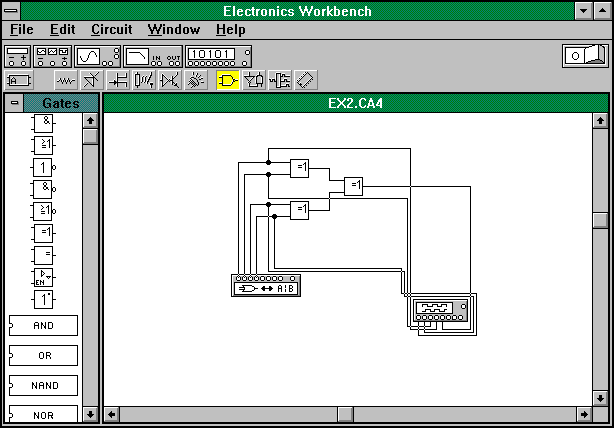
... И-НЕ. Для выполнения этой операции (при имеющемся в окошке булевом выражении) следует “нажать” стрелкой кнопку: 3. Математические модели и эквивалентные схемы в программе логического проектирования Любой реальный логический элемент(ЛЭ) не мгновенно реагирует на изменения входных сигналов, поэтому имеется некоторая паразитная задержка между моментом времени, в который на его входы поступают новые ...
... значение функции равно единице, а ноль не ставится, а для КСНФ – наоборот. Диаграмма для двух логических переменных (для ДСНФ): Для трех переменных: Карты Карно используются для ручной минимизации функций алгебры логики при небольшом количестве переменных. Правило минимизации: склеиванию подвергаются 2,4,8,16, клеток и клетки, лежащие на границе карты. При числе переменных 5 и ...

1 комментарий