Навигация
Минимизация функций алгебры логики
21878
знаков
27
таблиц
4
изображения
Минимизация ФАЛ
Совершенно нормальные формы хотя и дают однозначные представления функции, но являются очень громоздкими. Реализация СНФ программно или схемотехнически является избыточной, что ведет к увеличению программного кода, поэтому существуют методы упрощения логической записи – минимизации.
Определение: Преобразование логических функций с целью упрощения их аналитического представления называются минимизацией.
Существуют два направления минимизации:
1. Кратчайшая форма записи (цель – минимизировать ранг каждого терма). При этом получаются кратчайшие формы КДНФ, ККНФ, КПНФ.
2. Получение минимальной формы записи (цель – получение минимального числа символов для записи всей функции сразу).
При этом следует учесть, что ни один из способов минимизации не универсален!
Существуют различные методы минимизации:
1. Метод непосредственных преобразований логических функций. (1.1)
При применении данного метода:
а) Записываются ДСНФ логических функций
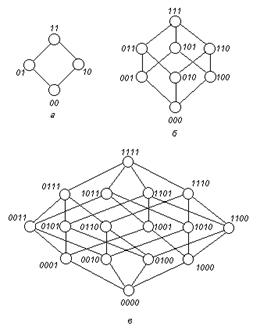
б) Форма преобразуется и упрощается с использованием аксиом алгебры логики. При этом, в частности, выявляются в исходном ДСНФ так называемые соседние min-термы, в которых есть по одной не совпадающей переменной.
По отношению к соседним min-термам применяется закон склейки, значит ранг min-терма понижается на единицу.
Определение: Min-термы, образованные при склеивании называются импликантами.
Полученные после склейки импликанты по возможности склеивают до тех пор, пока склеивание становится невозможным.
Определение: Несклеивающиеся импликанты называются прослойками.
Определение: Формула, состоящая из простых импликант – тупиковая.
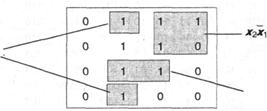
Пример:
|
|
|
|
|
|
| 0 | 0 | 0 | 1 | |
| 0 | 0 | 1 | 1 | |
| 0 | 1 | 0 | 1 | |
| 0 | 1 | 1 | 1 | |
| 1 | 0 | 0 | 0 | |
| 1 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | |
| 1 | 1 | 1 | 0 |
Если в процессе склейки образуется форма R, содержащая члены вида 
и 
то для нее справедливо выражение 
, что позволяет добавить к исходной форме R несколько членов вида пар и 
и после этого продолжить минимизацию.
Пример:
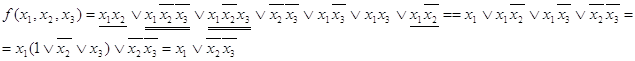
Мы получили минимальную СНФ.
Метод неопределенных коэффициентов. (1.2)
Суть метода состоит в преобразовании ДСНФ в МДНФ.
На основании теоремы Жигалкина любую ФАЛ можно представить в виде (рассмотрим на примере трех переменных):
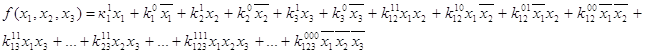
Алгоритм определения коэффициентов:
1. Исходное уравнение разбить на систему уравнений, равных числу строк в таблице истинности.
2. Напротив каждого выражения поставить соответствующее значение функции.
3. Выбрать строку, в которой значение функции 
и приравнять все 
к нулю.
4. Просмотреть строки, где функция имеет единичное значение, и вычеркнуть все коэффициенты, встречающиеся в нулевых строках.
5. Проанализировать оставшиеся коэффициенты в единичных строках.
6. Используя правило, что дизъюнкция равна 1 если хотя бы один из 
, выбрать min-термы минимального ранга. Причем отдавать предпочтение коэффициентам, встречающимся в нескольких уравнениях одновременно.
Похожие работы
... 0 и 1: . 10. Законы Блейка-Порецкого: . 11. Связь импликации с отрицанием – и дизъюнкцией : . 12. Связь эквивалентности ~ с дизъюнкцией , конъюнкцией и отрицанием: ~ y =. Всякая функция алгебры логики может быть реализована некоторой формулой языка с символами ~, –. 1.2 Дизъюнктивные и конъюнктивные нормальные формы (ДНФ и КНФ) ДНФ и КНФ играют особую роль в алгебре ...
... схемами с односторонней проводимостью, имеющими конечное число входов и один выход. Простейшие электронные схемы, реализующие элементарные булевы функции (НЕ, И, ИЛИ, ИЛИ-НЕ, И-НЕ), называются логическими элементами (ЛЭ). Аналитическая форма представления булевых функций При решении конкретных технических задач булевы функции, отражающие логические связи, наиболее часто задаются в табличной ...
... ответ на этот вопрос положителен. Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности. М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики. Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник ...
... , и, обратно, для любого автомата Мура существует эквивалентный ему автомат Мили. Таким образом, возможны взаимные трансформации автоматов. Граф-дерево автомата Мили. 10 В ходе этапа построения кодопреобразователя осуществляется преобразование графа-дерево автомата Мура в граф-дерево автомата Мили. Для этого все конечные состояния автомата Мура заменяются нулевым состоянием. Граф-дерево ...
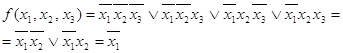
0 комментариев