Набор ЛЭ, с помощью которого можно реализовать сколь угодно сложную функцию, называется функционально полным или базисом. Например, ЛЭ И, ИЛИ, НЕ составляют базис. Имеются базисы, которые содержат только один ЛЭ. Это ЛЭ И-НЕ или ИЛИ-НЕ. Базис из элементов И-НЕ более популярен. Схема, составленная с использованием ЛЭ И, ИЛИ, НЕ удобнее для чтения, но схема, реализованная в базисе, состоящим из одного элемента, имеет часто меньше корпусов микросхем ЛЭ.
При переходе к базису И-НЕ или ИЛИ-НЕ используют правило де Моргана
Для практического использования более удобны формулы:
Правило де Моргана можно распространить на любое число переменных с помощью законов композиции.
Тождества и теоремы алгебры логики применяются для преобразования и упрощения выражения функций. Тождества применяются также и при доказательстве теорем. Теоремы и тождества в алгебре логики доказываются методом перебора всех значений переменных с использованием аксиом алгебры логики.
Практическое значение имеют тождества:
К логическим функциям применимы также законы:
коммутативный (переместительный)
Х 2 V Х 1 = Х 1 V Х 2 Х 2 • Х 1 = Х 1 • Х 2 ,
ассоциативный (сочетательный)
(Х 3 V Х 2) V Х 1 = Х 3 V (Х 2 V Х 1) (Х 3 •Х2) • Х 1 = Х3 • (Х 2 • Х 1)
дистрибутивный
Х 3 • ( Х2 V Х 1 ) = Х 3 • Х 2 V Х 3 • Х1
Х 3 V ( Х2 • Х 1 ) = ( Х3 V Х 2 ) • (Х 3 V Х 1 ) ,
двойного отрицания
В алгебре логики при отсутствии в выражении скобок вводится следующий порядок действий: первыми выполняются операции отрицания, далее – конъюнкции, затем – дизъюнкции. При наличии в первую очередь должны выполняться операции внутри скобок.
Применение тождеств для доказательства законов и теорем рассмотрим на примере доказательства соблюдения дистрибутивного закона Х 3 V( Х 2 • Х 1 ) = ( Х 3 VХ 2 ) • (Х 3 V Х 1 ). После раскрытия скобок в правой части получаем:
Х3 • Х 3 V Х 3 •Х1 V Х 3 •Х 2 VХ 2 •Х 1 .
Далее используем тождество .
Х 3 VХ 3 •Х 1 V Х 3 •Х 2 V Х 2 •Х1.
Используем тождество
Х3 • 1 V Х 3 •Х1 V Х 3 •Х 2 VХ 2 •Х 1.
Выносим за скобку Х 3
Х 3 ( 1 V Х 1 ) VХ 3 •Х 2 V Х 2 •Х 1.
Используем тождество
Х3 • 1 V Х 3 •Х2 V Х 2 •Х 1.
Вновь выносим за скобку
Х 3. Х3 (1 V Х 2 ) VХ 2 •Х 1.
Вновь используем тождество .
Х 3 • 1 VХ 2 •Х 1.
Вновь используем тождество .
Х3 V Х 2 •Х1.
Полученное выражение совпадает с левой частью исходного соотношения. Таким образом, истинность дистрибутивного закона доказана.
Особое место в алгебре логики занимает закон двойственности, сформулированный Шенноном. Закон позволяет определить инверсию любой функции и имеет вид:
,
где 
, 
. Таким образом, инверсию любой функции можно получить, если заменить в выражении функции переменные 
их инверсией 
и наоборот, и осуществить взаимную замену операций дизъюнкции и конъюнкции. Например, если
то 
Практическое применение имеет частный случай закона двойственности – теорема де Моргана:
Или в более удобном для практического использования виде
Теорема де Моргана используется на практике для перевода функции в заданный базис, а также при необходимости для замены операции дизъюнкции на конъюнкцию или наоборот. Например, необходимо, чтобы выражение содержало только операции дизъюнкции. После применения правила де Моргана получится. Теорему де Моргана можно распространит и на большее число переменных.
Похожие материалы
... значение функции равно единице, а ноль не ставится, а для КСНФ – наоборот. Диаграмма для двух логических переменных (для ДСНФ): Для трех переменных: Карты Карно используются для ручной минимизации функций алгебры логики при небольшом количестве переменных. Правило минимизации: склеиванию подвергаются 2,4,8,16, клеток и клетки, лежащие на границе карты. При числе переменных 5 и ...
... X3X4 V X1X2X4 V X1X2X4. Дальнейшее преобразование невозможно. Полученную функцию можно немного упростить с помощью вынесения за скобки общих переменных. 1.3.2 Метод Квайна При минимизации по методу Квайна предполагается, что минимизируемая логическая функция задана в виде ДСНФ. Здесь используется закон неполного склеивания. Минимизация проводится в два этапа: нахождение простых импликант, ...
... — f(x1,x2,x3,x4) = 3-йэтап—f(x1,x2,x3,x4)= что и требовалось получить. Проверить правильность проведенных преобразований можно при помощи правила склеивания. 3. Функционально полные системы логических функций. Анализ принадлежности переключательных функций замкнутым классам показывает, что существуют две переключательные функции f8 и f14, не принадлежащие ни одному классу. Согласно теореме ...
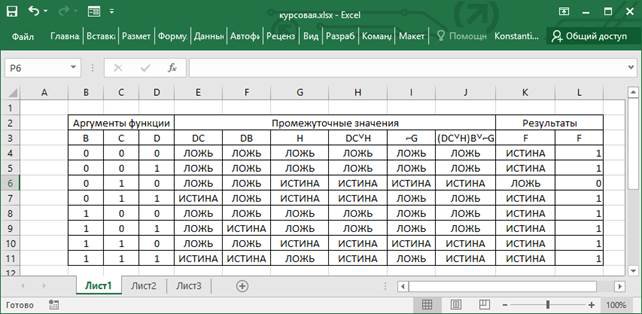
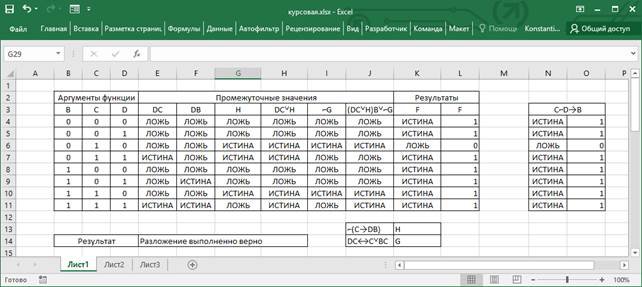
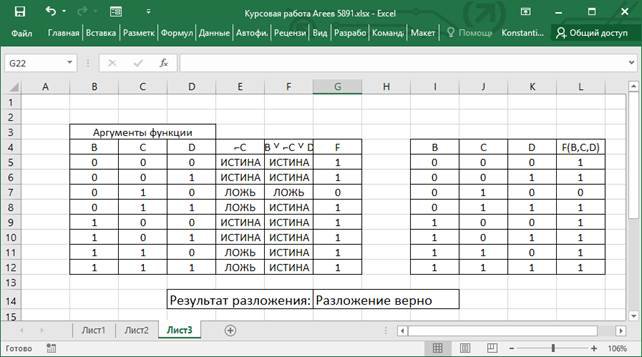
... , эквивалентности столбца аргументов DC и результата функции И столбцов аргументов С и ВС.Функции эквивалентности также нет в списке логических функций, реализуемых в Excel, поэтому эту функцию необходимо реализовать с использованием функции ЕСЛИ. Для 4 строки формула выглядит следующим образом f(x)=НЕ(ЕСЛИ(И(D4;C4)=ИЛИ(C4;И(B4;C4));ИСТИНА;ЛОЖЬ)). Столбец (DCH)B0G реализует функцию И, использую ...
0 комментариев