Навигация
Аппроксимация диаграммы деформирования при сложном напряженном состоянии
2.2 Аппроксимация диаграммы деформирования при сложном напряженном состоянии
На основании многочисленных экспериментальных данных, полученных в условиях пропорционального нагружения, было установлено, что с достаточной для инженерных расчетов степенью точности диаграмму деформирования материала независимо от вида напряженного состояния можно описать с помощью зависимости, получившей название обобщенной кривой деформирования
![]()
При существенно неупругом деформировании эту кривую можно аппроксимировать по Рамбергу-Осгуду степенной функцией вида
![]()
где
![]() –
–
–интенсивность напряжений (![]() –главные напряжения);
–главные напряжения);
![]() –
–
–интенсивность логарифмической пластической деформации;
![]() –главные логарифмические пластические деформации;
–главные логарифмические пластические деформации;
![]() – главные пластические деформации.
– главные пластические деформации.
Если интенсивности напряжения и деформации определяются зависимостями (10) и (11) (как известно, это не единственно возможный вариант), значения показателя упрочнения m и коэффициента прочности материала K будут совпадать с величинами, полученными в результате аппроксимации аналогичной степенной функцией кривой деформирования при растяжении.
В ряде случаев (например, при сопоставлении прочностных и деформационных свойств различных материалов) единую кривую удобно представлять в относительных величинах 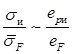 . В такой форме её легко получить, разделив левую и правую часть равенства (9) на соответствующие части выражения (7):
. В такой форме её легко получить, разделив левую и правую часть равенства (9) на соответствующие части выражения (7):
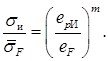
Для получения зависимости (12) по заданным точкам
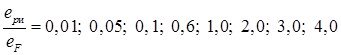
строим аппроксимацию единой диаграммы деформирования (рисунок 1).
Положение точек на единой кривой деформирования, соответствующих предельным значениям интенсивностей напряжений и деформаций в момент разрушения при различных видах напряженного состояния, определим с помощью деформационного критерия, записанного в терминах напряжений:
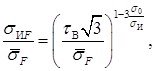
где
![]() – среднее напряжение;
– среднее напряжение;
![]() – интенсивность напряжений в момент разрушения.
– интенсивность напряжений в момент разрушения.
Зная параметры напряженного состояния (таблица 5), по зависимости (13), используя данные таблицы 1, находим отношение ![]() .
.
Таблица 5 – Параметры напряженного состояния, соответствующие различным видам нагружения
|
Растяжение |
Сжатие |
Чистый сдвиг |
Равноосное плоское растяжение |
Равноосное плоское сжатие |
Объемное растяжение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Затем из зависимости (12) находим отношение ![]() . Таким образом, находим координаты точек на единой кривой деформирования, соответствующие разрушающим значениям интенсивности напряжений и деформаций при заданных видах напряженного состояния (таблица 5).
. Таким образом, находим координаты точек на единой кривой деформирования, соответствующие разрушающим значениям интенсивности напряжений и деформаций при заданных видах напряженного состояния (таблица 5).
Результаты расчета представлены в таблице 6 и нанесены на единую кривую деформирования (рисунок 1). Для представления результатов ресурс пластичности определялся по формуле 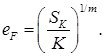
Таблица 6 – Параметры напряженного состояния, соответствующие различным видам нагружения
|
Параметр |
Растяжение |
Сжатие |
Чистый сдвиг |
Равноосное плоское растяжение |
Равноосное плоское сжатие |
Объемное растяжение |
|
|
1,00 |
1,16 |
1,08 |
0,93 |
1,26 |
0,71 |
|
|
1,00 |
3,04 |
1,74 |
0,57 |
5,29 |
0,08 |

Рисунок 1. Единая кривая деформирования алюминиевого сплава Д16Т и точки, отвечающие моменту разрушения при различных видах напряженного состояния
Анализируя график, представленный на рисунке 1, можно заметить, что напряженные состояния, которым соответствуют точки 1...6 на обобщенной кривой деформирования, располагаются в порядке уменьшения "жесткости" напряженного состояния. "Жесткость" 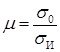 – параметр, характеризующий вид напряженного состояния. С уменьшением "жесткости" напряженного состояния возрастает интенсивность соответствующей логарифмической деформации в момент разрушения. Следовательно, чем напряженное состояние "жестче", тем больше вероятность хрупкого разрушения.
– параметр, характеризующий вид напряженного состояния. С уменьшением "жесткости" напряженного состояния возрастает интенсивность соответствующей логарифмической деформации в момент разрушения. Следовательно, чем напряженное состояние "жестче", тем больше вероятность хрупкого разрушения.
В точке 5, где соответствующее напряженное состояние является самым "мягким" из отмеченных на кривой деформирования, моменту разрушения соответствует интенсивность логарифмической пластической деформации в 5,3 раз больше ресурса пластичности материала при линейном напряженном состоянии. Интенсивность напряжений при этом в 1,26 раза превышает истинное сопротивление разрыву.
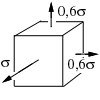
Самым опасным является напряженное состояние, которому соответствует точка 6 (объемное растяжение с соотношением компонент 1:0,6:0,6). В этом случае моменту разрушения соответствует интенсивность логарифмической пластической деформации, составляющая 8% от ресурса пластичности материала при линейном напряженном состоянии. Интенсивность напряжений при этом составляет 71% истинного сопротивления разрыву.
Похожие работы
... при одновременном воздействии механических напряжений возникают коррозионные очаги, изменяются твёрдость и упругость металла, приводящие к быстрому изнашиванию инструмента и дальнейшему разрушению [5, с.7]. Поэтому инструменты медицинские металлические должны быть коррозионностойкими, способными выдерживать воздействие температуры и влажности воздуха в условиях эксплуатации, транспортирования и ...
... что обнаруженный эффект в значительной степени можно отнести за счет концентрационной неоднородности твердого раствора. Это имеет место, например, в образцах, закалке с высокой температуры. Очевидно, что при повышении температуры нагрева от 1150 до 1200 ºС влияние неоднородности твердого раствора на образование микронапряжений из-за дополнительного растворения избыточной фазы больше, чем ...
... по условиям безопасности движения или взаимодействия автомобиля с дорогой; ¾ диагностика автомобильных дорог и дорожных сооружений ¾ обследование, сбор и анализ информации о параметрах, характеристиках и условиях работы, определяющих их транспортно-эксплуатационное состояние, необходимых для оценки, выявления причин и прогнозу возможных нарушений нормального функционирования дорог; ...
... передаточных чисел Кинематическое передаточное число ix: Силовое передаточное число iy: iy=F1/N¢V=2754,82/2596,5=1,061. 6.3 Построение кривой жесткости подвески Для построения упругой характеристики подвески автомобиля ЗАЗ-1102 “Таврия” необходимо определить жесткость средней части подвески с1. Расчет жесткости подвески с1 проводится по выбранной частоте колебаний ω ...
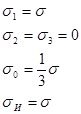
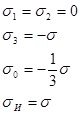
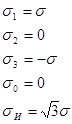
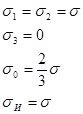
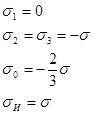
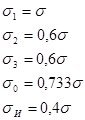
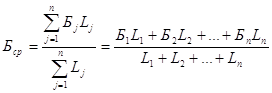
0 комментариев