Навигация
Определение поверхностей разрушения по деформационному критерию
3.3 Определение поверхностей разрушения по деформационному критерию
Деформационный подход к разработке критериев разрушения был развит в теоретических и экспериментальных исследованиях В.Л. Колмогорова с сотрудниками, в результате чего удалось сформулировать один из наиболее адекватных критериев вязкого разрушения. На основе обобщения весьма представительной выборки экспериментальных данных так называемый деформационный критерий устанавливает связь между предельной неупругой деформацией и специальной характеристикой напряженного состояния, которую авторы назвали параметром жесткости напряженного состояния, представляющим собой отношение среднего напряжения ![]() к интенсивности напряжений
к интенсивности напряжений ![]() (10).
(10).
Дальнейший анализ показал, что экспериментальные зависимости предельной интенсивности деформации ![]() от отношения
от отношения ![]() могут быть с достаточной для практических целей точностью аппроксимированы экспоненциальной функцией, содержащей два параметра
могут быть с достаточной для практических целей точностью аппроксимированы экспоненциальной функцией, содержащей два параметра
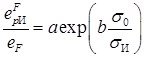
(данная формулировка деформационного критерия предложена К.М. Кононовым). Используя уравнение единой кривой (9), связывающей интенсивности напряжений и деформаций, последнее выражение можно привести к виду
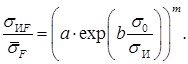
Для определения постоянных a и b достаточно данных двух экспериментов, выполненных при простых видах нагружения – растяжении и чистом сдвиге.
При растяжении имеем 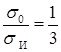 ,
, ![]() ; тогда из формулы (19) следует, что a и b взаимосвязаны:
; тогда из формулы (19) следует, что a и b взаимосвязаны:
![]()
При чистом сдвиге –  ,
, ![]() – получим
– получим
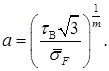
Интенсивность предельной пластической деформации в этом случае есть 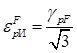 (
(![]() – пластическая деформация сдвига в момент разрушения).
– пластическая деформация сдвига в момент разрушения).
Для алюминиевого сплава Д16Т получаем
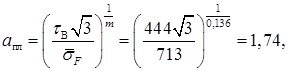
![]()
С учетом (20) и (21) выражение (19) можно представить в довольно простой форме (13), использованной в подразделе 2.2,
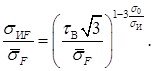
С помощью полученной выше зависимости и опытных данных ![]() можно найти предельную интенсивность напряжений
можно найти предельную интенсивность напряжений ![]() и соответствующую ей интенсивность деформаций для рассматриваемого материала (9)
и соответствующую ей интенсивность деформаций для рассматриваемого материала (9)
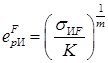
при произвольном напряженном состоянии.
Формулы (13) и (22) удобно использовать, определяя например, координаты точек на единой кривой деформирования, отвечающих моменту разрушения.
Сопоставляя формулу (15) с учетом определений (20), (21) с общей формулой критериев разрушения ![]() , заключаем, что выражение для эквивалентного напряжения по деформационному критерию принимает вид
, заключаем, что выражение для эквивалентного напряжения по деформационному критерию принимает вид
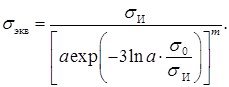
Примечательно, что согласно данному критерию существует однозначная связь между основными характеристиками прочности. Поскольку при одноосном сжатии 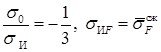 , из равенства (13) следует
, из равенства (13) следует
![]()
откуда нетрудно по известным двум характеристикам получить значение третьей, а также величину коэффициента разнопрочности для пластичного материала
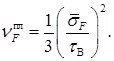
Для алюминиевого сплава Д16Т
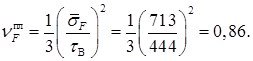
Несколько проще обстоит дело с хрупкими и малопластичными материалами. Не внося существенной погрешности, можно считать, что они работают упруго вплоть до разрушения, иными словами, обладают линейной диаграммой деформирования. В этой ситуации для её описания нет необходимости, как прежде, использовать истинное напряжение – достаточно условного, а логарифмическую пластическую деформацию вполне заменит обычное относительное удлинение:
![]()
(очевидно, показатель упрочнения ![]() ).
).
Привлекая для определения постоянных a и b деформационного критерия в форме (19) данные испытаний на растяжение (см. выше), получим соотношение между ними аналогичное (20)
![]()
с помощью результатов испытаний на сжатие – величину a:
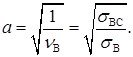
Для ковкого чугуна КЧ 35-10 получаем следующие значения констант a и b:
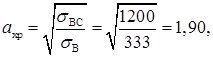
![]()
Поверхность разрушения построена в относительных координатах 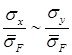 аналогично поверхности разрушения, полученной в подразделе 3.1
аналогично поверхности разрушения, полученной в подразделе 3.1
Результаты расчета для алюминиевого сплава Д16Т и ковкого чугуна ![]() представлены в таблице 9 и проиллюстрированы рисунком 4.
представлены в таблице 9 и проиллюстрированы рисунком 4.
|
Вид напряженного состояния |
Главные напряжения |
|
|
Д16Т |
КЧ 35-10 |
||||
|
|
|
|
|
|
|
||||
|
|
|
0,67 |
1,00 |
1,08 |
0,93 |
0,93 |
1,90 |
0,53 |
0,53 |
|
|
|
0,50 |
0,87 |
0,92 |
1,10 |
0,55 |
1,39 |
0,72 |
0,36 |
|
|
|
0,33 |
1,00 |
1,00 |
1,00 |
0,00 |
1,00 |
1,00 |
0,00 |
|
|
|
0,17 |
1,32 |
1,26 |
0,80 |
-0,40 |
0,89 |
1,13 |
-0,56 |
|
|
|
0 |
1,73 |
1,61 |
0,62 |
-0,62 |
0,91 |
1,10 |
-1,10 |
|
|
|
-0,17 |
1,32 |
1,19 |
0,42 |
-0,84 |
0,55 |
0,91 |
-1,83 |
|
|
|
-0,33 |
1,00 |
0,86 |
0,00 |
-1,16 |
0,28 |
0,00 |
-3,60 |
|
|
|
-0,5 |
0,87 |
0,70 |
-0,71 |
-1,42 |
0,15 |
-3,33 |
-6,65 |
|
|
|
-0,67 |
1,00 |
0,80 |
-1,26 |
-1,26 |
0,15 |
-6,84 |
-6,84 |
Таблица 9 – Координаты точек поверхностей разрушения алюминиевого сплава Д16Т и ковкого чугуна КЧ 35-10, полученные по деформационному критерию
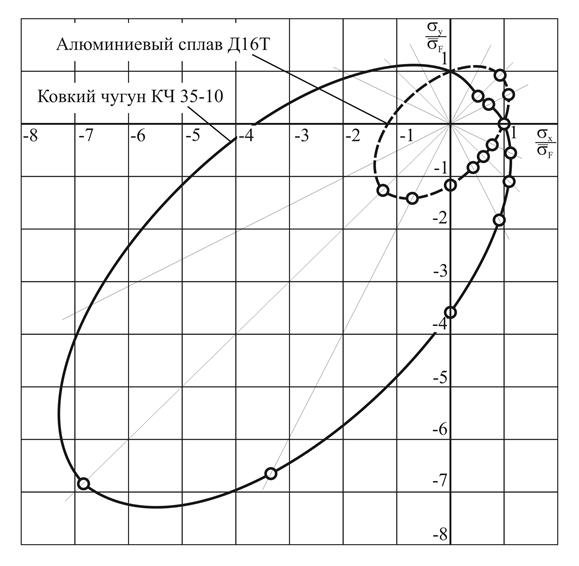
Рисунок 4 – Поверхности разрушения пластичного и хрупкого материала, полученные по критерию Лебедева-Писаренко
Особенность деформационного критерия по сравнению с рассмотренными ранее состоит в том, что им отражается более существенное снижение прочности при двух- или трехосном растяжении и, в ряде случаев, наоборот, её повышение при одноосном сжатии.
Похожие работы
... при одновременном воздействии механических напряжений возникают коррозионные очаги, изменяются твёрдость и упругость металла, приводящие к быстрому изнашиванию инструмента и дальнейшему разрушению [5, с.7]. Поэтому инструменты медицинские металлические должны быть коррозионностойкими, способными выдерживать воздействие температуры и влажности воздуха в условиях эксплуатации, транспортирования и ...
... что обнаруженный эффект в значительной степени можно отнести за счет концентрационной неоднородности твердого раствора. Это имеет место, например, в образцах, закалке с высокой температуры. Очевидно, что при повышении температуры нагрева от 1150 до 1200 ºС влияние неоднородности твердого раствора на образование микронапряжений из-за дополнительного растворения избыточной фазы больше, чем ...
... по условиям безопасности движения или взаимодействия автомобиля с дорогой; ¾ диагностика автомобильных дорог и дорожных сооружений ¾ обследование, сбор и анализ информации о параметрах, характеристиках и условиях работы, определяющих их транспортно-эксплуатационное состояние, необходимых для оценки, выявления причин и прогнозу возможных нарушений нормального функционирования дорог; ...
... передаточных чисел Кинематическое передаточное число ix: Силовое передаточное число iy: iy=F1/N¢V=2754,82/2596,5=1,061. 6.3 Построение кривой жесткости подвески Для построения упругой характеристики подвески автомобиля ЗАЗ-1102 “Таврия” необходимо определить жесткость средней части подвески с1. Расчет жесткости подвески с1 проводится по выбранной частоте колебаний ω ...
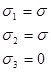
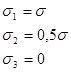
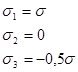
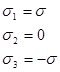
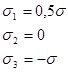
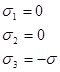

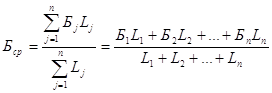
0 комментариев