=±Ö1-sin2a=(1-tg2a/2)/(1+tg2a/2) | sina=±Ö1/1+ctg2a=(2tga/2)/(1+tg2a/2) |
| cos(a | sin(a±b)=sinacosb±sinbcosa |
| tg(a+b)=sin(a+b)/cos(a+b)=(tga+tgb)/(1-tgatgb) | tg(a-b)=(tga-tgb)/(1+tgatgb) |
| ctg(a+b)=(ctgactgb-1)/(ctga+ctgb) | ctg(a-b)=(ctgactgb+1)/(ctgb-ctga) |
| sin2a=2sinacosa=(2tga)/(1+tg2a) | cos2a=cos2a-sin2a=(1-tg2a)/(1+tg2a)=2cos2a-1=1-2sin2a |
| tg2a=2tga/(1-tg2a) ctg2a=(ctg2a-1)/2ctga | ctg2a=(ctg2a-1)/2ctga |
| cos2a/2=1+cosa/2 cos2a=(1+cos2a)/2 | sin2a/2=1-cosa/2 sin2a=(1-cos2a)/2 |
| cosa/2=±Ö1+cosa/2 | sina/2=±Ö1-cosa/2 |
| tga/2=±Ö1-cosa/1+cosa=(sina)/(1+cosa)=(1-cosa)/sina | ctga/2=±Ö1+cosa/1-cosa=sina/(1-cosa)=(1+cosa)/sina |
| sina+cosa=Ö2 cos(P/4-a) | sina-cosa=Ö2 sin(a-P/4) |
| cosa-sina=Ö2 sin(P/4-a) | cosa+cosb=2cos(a+b)/2cos(a-b)/2 |
| cosa-cosb=-2sin(a+b)/2sin(a-b)/2 | sina+sinb=2sin(a+b)/2cos(a-b)/2 |
| sina-sinb=2sin(a-b)/2cos(a+b)/2 | tga±tgb=(sin(a±b))/cosacosb |
| cosacosb=1/2(cos(a-b)+cos(a+b)) | sinasinb=1/2(cos(a-b)-cos(a+b)) |
| sinacosb=1/2(sin(a+b)+sin(a-b)) | tga=(2tga/2)/(1-tg2a/2) |
| cosa=±Ö1-sin2a=(1-tg2a/2)/(1+tg2a/2) | sina=±Ö1/1+ctg2a=(2tga/2)/(1+tg2a/2) |
| cos(a | sin(a±b)=sinacosb±sinbcosa |
| tg(a+b)=sin(a+b)/cos(a+b)=(tga+tgb)/(1-tgatgb) | tg(a-b)=(tga-tgb)/(1+tgatgb) |
| ctg(a+b)=(ctgactgb-1)/(ctga+ctgb) | ctg(a-b)=(ctgactgb+1)/(ctgb-ctga) |
| sin2a=2sinacosa=(2tga)/(1+tg2a) | cos2a=cos2a-sin2a=(1-tg2a)/(1+tg2a)=2cos2a-1=1-2sin2a |
| tg2a=2tga/(1-tg2a) ctg2a=(ctg2a-1)/2ctga | ctg2a=(ctg2a-1)/2ctga |
| cos2a/2=1+cosa/2 cos2a=(1+cos2a)/2 | sin2a/2=1-cosa/2 sin2a=(1-cos2a)/2 |
| cosa/2=±Ö1+cosa/2 | sina/2=±Ö1-cosa/2 |
| tga/2=±Ö1-cosa/1+cosa=(sina)/(1+cosa)=(1-cosa)/sina | ctga/2=±Ö1+cosa/1-cosa=sina/(1-cosa)=(1+cosa)/sina |
| sina+cosa=Ö2 cos(P/4-a) | sina-cosa=Ö2 sin(a-P/4) |
| cosa-sina=Ö2 sin(P/4-a) | cosa+cosb=2cos(a+b)/2cos(a-b)/2 |
| cosa-cosb=-2sin(a+b)/2sin(a-b)/2 | sina+sinb=2sin(a+b)/2cos(a-b)/2 |
| sina-sinb=2sin(a-b)/2cos(a+b)/2 | tga±tgb=(sin(a±b))/cosacosb |
| cosacosb=1/2(cos(a-b)+cos(a+b)) | sinasinb=1/2(cos(a-b)-cos(a+b)) |
| sinacosb=1/2(sin(a+b)+sin(a-b)) | tga=(2tga/2)/(1-tg2a/2) |
Похожие работы
... решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n - ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с ...
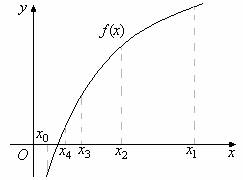
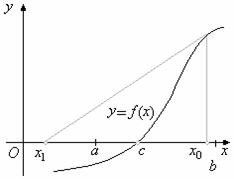
... - в методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики ...
... образом, обращение с числовым рядом как с величиной позволяет по новому формировать сами навыки сложения-вычитания (а затем умножения-деления). Глава II. Методические рекомендации к изучению алгебраического материала в начальной школе 2.1 Обучение в начальной школе с точки зрения потребностей средней школы Как известно, при изучении математики в 5-м классе существенная часть времени ...
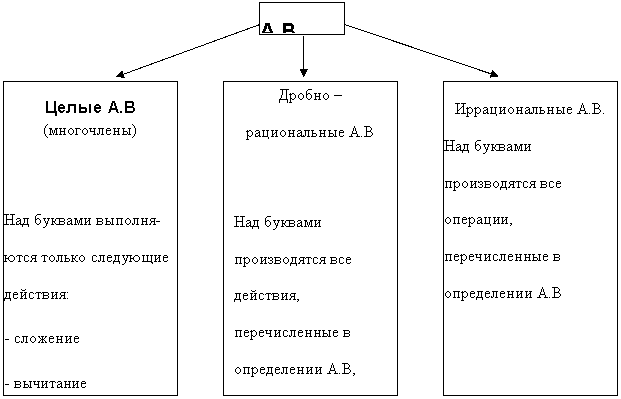
... для численных расчетов или дальнейших преобразований. К Т.П относятся: приведение подобных членов раскрытие скобок разложение на множители приведение алгебраических дробей к общему знаменателю избавление от иррациональности в знаменателе и т.п. 2. Рассмотрим тождественные преобразования А.В. Для успешного осуществления Т.П. целых А.В нужно помнить: Формулы сокращенного умножения (a ± b)2 = a2 + ...

0 комментариев