Навигация
Решение алгебраического уравнения n-ой степени
B.А. Будников
Б 903 Решение алгебраического уравнения n-ой степени - Новосибирск: Интернет, Блоги: budnikov57@mail.ru, 2010. - 26 с.
В работе предложено аналитическое решение (в радикалах) алгебраического уравнения n - ой степени. Решены Проблемы собственных значений для нахождения Функций от Матриц и устойчивости решений линейных дифференциальных и разностных уравнений. Метод решения основан на последовательном получении алгебраического уравнения относительно квадратов независимой переменной и его Решении с последующим возвратом к корням исходного уравнения. Метод характеризуется простотой и требует только умения решать квадратные уравнения и извлекать корни n - ой степени из комплексного числа. Алгоритм решения легко поддаётся программированию. Приведены конкретные примеры решения алгебраических уравнений с третьей по восьмую степень включительно.
Статья может быть полезна Специалистам, занимающимся решением задач Высшей Алгебры, а также Студентам высших учебных заведений, интересующимся сложными математическими Проблемами.
Введение
Проблема решения в радикалах алгебраического уравнения произвольной степени, так называемого Векового уравнения, интересовала математиков всех времён и народов. Удача Тартальи и Феррари в решении уравнений третьей и четвёртой степеней внесла надежду на успехи в этом направлении и далее. Однако Решения долгое время найти не удавалось / 1/. Могу с уверенностью сказать, что все Великие математики, в течение последних пятисот лет, занимались решением уравнений высших степеней. Уравнение пятой степени решали Ньютон, Лейбниц, Лагранж, Эйлер, Гаусс, Тэйлор, Абель, Галуа, Пуанкаре, Клейн, Гильберт и многие другие (Список можно было бы ещё долго продолжать). В справочниках по высшей Математике сказано, что НЕ СУЩЕСТВУЕТ решения в радикалах алгебраических уравнений выше четвёртой степени / 2/. Казалось бы, не существует и решать не надо! Однако в Технике очень важно выбирать параметры Систем в соответствие с принципами Оптимальности, чтобы Объекты, описываемые системами дифференциальных или разностных уравнений, удовлетворяли заданному Критерию качества (например, минимуму потребляемой Энергии или максимальному быстродействию).
Для пояснения дальнейших рассуждений введём систему условных обозначений.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ:
* - знак умножения,
** - знак возведения в степень,
ABS (x) - абсолютная величина комплексной переменной x,
Re x, Im x - действительная и мнимая величины комплексной переменной x соответственно,
Mod x, Fi x - модуль и угол комплексной переменной x соответственно,
SIN (x), COS (x) - тригонометрические функции sinx и cosx,
ARCTAN (Im x, Re x) - обратная тригонометрическая функция arctg ( (Im x) / (Re x)).
SQRT (x) - операция извлечения квадратного корня из действительного числа x.
PI = 3.141592653589793 - число π.
В 1683 году друг Г.В. Лейбница Э.В. фон Чирнгауз (1651 - 1708) опубликовал в журнале "Acta Eruditorum" метод преобразования алгебраического уравнения в уравнение той же степени с меньшим числом членов.
Чирнгауз из уравнения
(x**n) + A1* (x** (n - 1)) + A2* (x** (n - 2)) + … + An = 0,
и уравнения с неопределёнными коэффициентами
y = B1* (x** (n - 2)) + B2* (x** (n - 3)) + … + Bn-1,
исключал x. Он полагал, что в полученном уравнении
(y**n) + C1* (y** (n - 1)) + C2* (y** (n - 2)) + … + Cn = 0,
можно будет подобрать коэффициенты Bi, от которых зависят Ci, так, что все коэффициенты Ci, кроме одного, обратятся в нуль. Тогда последнее уравнение примет вид
( y**n) + Cn = 0,
и исходное уравнение относительно переменной x будет разрешимо в радикалах.
Отметим, что в общем случае коэффициент Cn может быть комплексной величиной, для которой, в соответствие с теорией функций комплексного переменного, существуют понятия модуля и угла вектора на комплексной плоскости. Для упрощения рассуждений будем полагать коэффициент Cn действительной величиной ( (-Cn) > 0)
Пусть q = (-Cn) ** (1/n), тогда уравнение относительно переменной yi легко может быть решено
yi = q* (COS (2* (i - 1) *PI/ n) + j*SIN (2* (i - 1) *PI/ n),
где q - арифметический корень n - ой степени из числа (-Cn),
i - порядковый номер корня уравнения, i = 1, n;
j - квадратный корень из ( - 1), мнимая величина.
Выражение COS (2* (i - 1) *PI/ n) + j*SIN (2* (2* (i - 1) *PI/ n) задаёт корни уравнения
( (x**n) - 1) / (x - 1) = 1 + x + (x**2) + … + (x** (n - 1)) = 0.
Последнее представляет собой выражение для суммы n членов геометрической прогрессии с основанием x.
Чирнгаузу удалось решить таким образом уравнение при n = 3, но в общем случае приём к цели не приводил. Лейбниц, которому Чирнгауз сообщил письмом в 1677 году идею метода, заметил, что ничего не получается даже для уравнения пятой степени.
Исаак Ньютон (1643 - 1727) после безуспешных попыток точно решить уравнение пятой степени разработал приближённый метод численного определения действительного корня алгебраического уравнения произвольной степени, получивший его имя и используемый до сих пор (так называемый метод касательных Ньютона). Суть метода заключается в следующем: Предположим, что действительный корень заданного алгебраического уравнения y1 находится в интервале (a, b).
Вычисляют значение алгебраической функции F (a) или F (b), ( F (a) = (a**n) + A1* (a** (n - 1)) + A2* (a** (n - 2)) + …+ An ), записывают уравнение касательной в этой точке и определяют точку пересечения касательной с осью абсцисс, которой присваивают новое значение a или b.
Процесс вычислений выполняют до тех пор, пока не будет достигнута требуемая степень точности вычислений EPS (y1 = a или y1 = b в зависимости от того с какой стороны (слева или справа) решено приблизиться к корню y1).
Метод всегда сходится, но НИЧЕГО не говорит об оптимальных значениях коэффициентов уравнения, которые непосредственно связаны с параметрами Систем.
Следующий этап развития теории решения уравнений связан с творчеством Леонарда Эйлера (1707 - 1783), который, как и все предшественники, считал возможным решение уравнений любой степени.
Эйлер установил, что уравнения второй, третьей, четвёртой степеней сводятся к уравнениям первой, второй и третьей степеней, которые он назвал "разрешающими уравнениями", резольвентами.
Резольвенту приведённого кубического уравнения (x**3) + B2* x + B3 = 0, Эйлер получил, положив
x = (A** (1/ 3)) + (B** (1/ 3)).
Для приведённого уравнения четвёртой степени (x**4) + B2* (x**2) + B3*x + B4 = 0, он рекомендовал подстановку
x = (A** (1/ 4)) + (B** (1/ 4)) + (C** (1/ 4)).
Тем самым он открыл ДРУГОЙ способ решения уравнения четвёртой степени, отличный от решения Феррари.
Эйлер полагал, что приведённое уравнение n-ой степени
(x**n) + B2* (x** (n - 2)) + B3* (x** (n - 3)) + … + Bn = 0,
может быть решено с помощью подстановки
x = (A** (1/ n)) + (B** (1/ n)) + … + (G** (1/ n)),
где число слагаемых равно (n - 1). Им использовались и другие подстановки. Однако уравнение выше четвёртой степени Эйлеру решить не удалось.
При доказательстве невозможности решения уравнения пятой степени Н.Х. Абель (1802 - 1829) опирался на предложенную Эйлером подстановку
x = w + A* ( (v** (1/ 5)) + B* ( (v** (2/ 5)) + C* ( (v** (3/ 5)) + D* ( (v** (4/ 5)),
применив опыт великого Математика в своей работе.
Феликсом Клейном (1849 - 1925) написана монография / 3/, в которой наиболее полно показана сложность нахождения точного решения уравнения пятой степени. Книга содержит 336 страниц текста, а решения - нет! Оговорюсь сразу, что я вовсе не собираюсь принижать вклад Великих математиков в Науку, напротив, преклоняюсь перед их Волей и Настойчивостью при решении столь сложной Задачи. Они, как все лучшие представители Человечества, опережали своё Время. При отсутствии средств вычислительной техники все попытки были обречены: не было не только персональных компьютеров, но даже простых калькуляторов. Точность вычислений на логарифмической линейке для этой цели оставляла желать лучшего.
Мне удалось решить алгебраическое уравнение n - ой степени в радикалах, но Решение это - приближённое и требует вычислений с высокой степенью точности. За всё надо платить, бесплатно НИЧЕГО не даётся! Для определения корней уравнения не требуется знание интервала, где алгебраическая функция меняет свой знак (интервала нахождения действительного корня), что отличает разработанный Метод решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n - ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с любой степенью точности, если мощность персонального компьютера позволяет избежать влияния погрешностей округления на вычисления.
Отметим также, что с Решением Векового уравнения решаются Проблемы собственных значений при вычислении Функций от Матриц и Устойчивости решений линейных дифференциальных и разностных уравнений, описывающих движения сложных технических Объектов с постоянной и переменной структурой (например, вентильных преобразователей). В любом учебнике по Теории Автоматического Управления / 4/ можно прочитать: Решение линейного дифференциального уравнения устойчиво, если все корни характеристического уравнения лежат в левой полуплоскости комплексной плоскости корней. Решение разностного уравнения устойчиво, если все корни характеристического уравнения находятся внутри круга единичного радиуса на комплексной плоскости с центром в начале координат.
Оптимальное управление Системами требует отдельного рассмотрения. Скажу лишь, что Оптимальные параметры Систем могут быть достигнуты на Границе устойчивости.
Ниже приводятся СУТЬ метода Решения алгебраических уравнений и конкретные Примеры определения корней уравнений с третьей по восьмую степень включительно, доказывающие ПРАВИЛЬНОСТЬ полученных результатов и уже изложенные автором в других работах / 5, 6/.
ПОСТАНОВКА ЗАДАЧИ
Общий вид алгебраического уравнения n - ой степени
(x**n) + A1* (x** (n-1)) + A2* (x** (n-2)) + … + A (n-1) *x + An = 0, (1)
где
n - порядок алгебраического уравнения, ___
Ai - коэффициенты уравнения, любые действительные числа, i = 1,n.
Случай комплексных коэффициентов уравнения в данной работе не рассматривается.
Поскольку Вычисления на персональном Компьютере обладают конечной точностью, целесообразно уравнение (1) нормировать по старшему коэффициенту An, чтобы не происходило переполнения разрядной сетки. Нормирующий коэффициент RCn = (ABS (An)) ** (1/n). Если n - нечётная величина, знак абсолютной величины обычно опускают. Вычисления на персональном Компьютере всегда ведутся с определённой степенью точности EPS, которая задает Критерий окончания Счета.
Критерий окончания Счета: Если алгебраическая функция, заданная уравнением (1), при вычисленном значении корня xi меньше величины ABS (EPS*An), то вычисления названного корня прекращают. Далее понижают порядок исходного уравнения до величины (n - 1), если корень xi - действительный, или до величины (n - 2), если xi принадлежит паре комплексно - сопряжённых корней. Вся процедура повторяется сначала для полученного уравнения более низкого порядка до тех пор, пока не будут найдены все корни исходного уравнения (1). Если возможности Компьютера не достаточны, следует понизить степень точности EPS (в ущерб точности вычисления корней) или приобрести более мощную Персоналку. (Персоналка - персональная вычислительная Машина для каждого Пользователя)
Очевидно, что чем мощнее Компьютер, тем больше возможностей для решения уравнений более высоких Степеней n.
ЛОГИКА РАССУЖДЕНИЙ.
В общем случае, корни алгебраического уравнения отличаются друг от друга по величине. Следовательно, ВСЕГДА можно выделить в Решении наибольший по модулю (доминирующий) и наименьший корни. (Уместно оговориться сразу, что наименьший по модулю корень будет доминирующим в уравнении, обратном данному).
Попробуем последовательно возводить корни в квадрат и сравнивать их по величине между собой. После нескольких таких операций легко убедиться, что все корни уравнения для квадратов относительно переменной xc = (x** (2**J)) - ничтожно малы, кроме доминирующего корня xc1.
ВСЕ коэффициенты уравнения, кроме первых двух, будут стремиться к нулю и, следовательно, ими можно пренебречь. Тогда корень xc1 может быть найден из квадратного уравнения, а корень исходного алгебраического уравнения определится выражением x1 = (xc1** (1/ (2**J))).
Зачастую, при обеспечении заданной степени точности EPS, раньше вычисляется доминирующий корень обратного уравнения, поэтому РЕКОМЕНДУЕТСЯ определять доминирующие корни как прямого, так и обратного, уравнений.
При этом удаётся минимизировать затраты машинного времени и, следовательно, добиться максимальной скорости вычислений.
Уравнение (1) является частным случаем другого алгебраического уравнения n - ой степени для переменной xc = (x** (2**J)), где J - шаг преобразования, J = 1,m, m и n - любые натуральные числа.
(xс**n) + B1* (xс** (n-1)) + B2* (xc** (n-2)) + … + B (n-1) *xc + Bn = 0, (2)
где
B1 = - ( (C1**2) - (2*C2)),
B2 = (C2**2) - (2*C1*C3) + (2*C4),
B3 = - ( (C3**2) - (2*C2*C4) + (2*C1*C5) - (2*C6)),
………………………………………………………
B (n-1) = ( (-1) ** (n-1)) * ( (C (n-1) **2) - (2*C (n-2) *Cn)),
Bn = ( (-1) **n) * (Cn**2).
Уравнение (2) может быть получено умножением исходного уравнения (1) на уравнение для корней, взятых с обратным знаком. Например, для случая n = 3 это выглядит следующим образом:
( (x**3) + A1* (x**2) + A2*x + A3) * ( (x**3) - A1* (x**2) + A2*x - A3) = 0.
Тогда относительно переменной xc = (x**2) получают уравнение (2) при J = 1
(xc**3) - ( (A1**2) - (2*A2)) * (xc**2) + ( (A2**2) - (2*A1*A3)) *xc - (A3**2) = 0.
Не вызывает сомнений, что
J = 0, Bi = Ai, xc = x.
J = 1, Ci = Ai, xc = (x**2).
J = 2, Ci = Bi для J = 1, xc = (x**4).
………………………………………….
Пусть L = (2**J) - величина степени корня xc1 на J -ом шаге преобразования,
xc1 = (x1**L).
Как уже отмечалось выше, на определённом шаге преобразований J все коэффициенты уравнения (2), кроме первых двух B1 и B2, становятся пренебрежительно малы и их можно отбросить. Тогда корень xc1 может быть найден из квадратного уравнения, получаемого путём отбрасывания ничтожно малых старших коэффициентов. (Не следует забывать, что исходное уравнение (1) уже нормировано по старшему коэффициенту An).
(xc1**2) + D1* (xc1) + D2 = 0, (3)
D1 = B1, D2 = B2 - для прямого уравнения,
D1 = (Bn-1) / Bn, D2 = (Bn-2) / Bn - для обратного уравнения.
Совершенно очевидно
xc1 = ( - D1/ 2) + ( ( ( - D1/2) **2) - D2) ** (1/ 2),
или
xc1 = ( - D1/ 2) - ( ( ( - D1/ 2) **2) - D2) ** (1/ 2), (4)
Корень исходного уравнения
x1 = (xc1** (1/L)). (5)
Если алгебраическая Функция при вычисленном значении корня x1 F (x1) не удовлетворяет Критерию окончания Счета, переходят к следующему шагу преобразования (J присваивают значение J + 1) до тех пор, пока не будет достигнута требуемая точность вычислений EPS.
Уместно отметить, что величина xc1 может быть как действительной, так и комплексной величиной. При вычислении корня x1 следует подвергать Проверке ВСЕ КОРНИ степени L из переменной xc1:
Если xc1 - комплексная величина (общий случай), тогда
PI = 3.141592653589793, I2 = 1, L
Mod xc1 = SQRT ( (Re xc1) **2) + ( (Im xc1) **2)),
Fi xc1 = ARCTAN (Im xc1, Re xc1),
Re x1 = ( (Mod xc1) ** (1/L)) *COS ( ( (Fi xc1) /L) + (2*PI/L) *I2),
Im x1 = ( (Mod xc1) ** (1/L)) *SIN ( ( (Fi xc1) /L) + (2*PI/L) *I2).
Теорема:
Для любого алгебраического уравнения при заданной степени точности EPS всегда существует такая величина J, при которой корень квадратного уравнения (3) совпадает с одним из корней исходного уравнения (1).
При выборе формулы расчёта следует помнить, что
Если I1 = 1 или I1 = 2, то вычисление xc1 осуществляется по формуле (3) для прямого уравнения (2).
Если I1 = 3 или I1 = 4, то вычисление xc1 происходит по формуле (3) для уравнения, обратного уравнению (2).
Теорема может быть доказана с помощью Метода Математической Индукции.
В заключение отметим, что в работе / 5/ коэффициенты квадратного уравнения (3) определены несколько иначе, однако корни исходного алгебраического уравнения (1) вычисляются с той же степенью точности EPS. Ввиду того, что коэффициенты Аi алгебраического уравнения (1) являются независимыми переменными, но возможны и ЧАСТНЫЕ СЛУЧАИ, указать величину J заранее не представляется возможным. Программы, используемые для проверочных расчётов, составлены автором на алгоритмическом языке FORTRAN - 90 и доказали свою высокую Эффективность.
Проверка всегда позволяет избежать Ошибок.
ПРОВЕРКА.
Дано алгебраическое уравнение третьей степени
(x**3) - 11* (x**2) - 10*x + 200 = 0.
Решение:
Степень точности EPS = 0.00001.
Нормирующий коэффициент для исходного уравнения RC3 = 5,8480.
Коэффициент выбора формулы расчета I1 = 2.
I2 = 1
Порядковый номер преобразования J = 3
Корень x3 - действительный
x3 = 10,000.
Корни x1, x2 - действительные
x1 = 5,0000; x2 = - 4,0000.
Дано алгебраическое уравнение третьей степени
(x**3) - 25* (x**2) + 216*x - 580 = 0.
Решение:
Степень точности EPS = 0.00001.
Нормирующий коэффициент для исходного уравнения RC3 = - 8,3396.
Коэффициент выбора формулы расчета I1 = 4.
I2 = 5
Порядковый номер преобразования J = 3
Корень x3 - действительный
x3 = 5,0000.
Корни x1, x2 - комплексно-сопряжённые
Re x1 = 10,000; Im x1 = 4,0000;
Re x2 = 10,000; Im x2 = - 4,0000.
Дано алгебраическое уравнение четвёртой степени
(x**4) + 6* (x**3) - 57* (x**2) - 110*x + 600 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC4 = 4,9492.
Коэффициент выбора формулы расчета I1 = 2.
I2 = 5.
Порядковый номер преобразования J = 3.
Корень x4 - действительный
x4 = - 10,000.
Корень x3 - действительный
x3 = 5,0000.
Корни x1, x2 - действительные
x1 = 3,0000; x2 = - 4,0000.
Дано алгебраическое уравнение четвёртой степени
(x**4) + 0* (x**3) + 67* (x**2) - 808*x + 1740 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC4 = 6,4586.
Коэффициент выбора формулы расчета I1 = 3, I2 = 1.
Порядковый номер преобразования J = 3.
Корни x3, x4 - комплексно-сопряжённые
Re x3 = - 4,0000; Im x3 = 10,000;
Re x4 = - 4,0000; Im x4 = - 10,000;
Корни x1, x2 - действительные
x1 = 3,0000; x2 = 5,0000.
Дано алгебраическое уравнение четвёртой степени
(x**4) + 4* (x**3) - 66* (x**2) + 76*x + 1360 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC4 = 6,0727.
Коэффициент выбора формулы расчета I1 = 3.
I2 = 1
Порядковый номер преобразования J = 0
Корни x3, x4 - действительные
x3 = - 10.000; x4 = - 4.0000.
Корни x1, x2 - комплексно - сопряжённые
Re x1 = 5,0000; Im x1 = 3,0000;
Re x2 = 5,0000; Im x2 = - 3,0000.
Дано алгебраическое уравнение четвёртой степени
(x**4) - 2* (x**3) + 70* (x**2) - 888*x + 3944 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC4 = 7,9247.
Коэффициент выбора формулы расчета I1 = 3.
I2 = 15.
Порядковый номер преобразования J = 4.
Корни x3, x4 - комплексно - сопряжённые
Re x3 = 5,0000; Im x3 = 3,0000;
Re x4 = 5,0000; Im x4 = - 3,0000;
Корни x1, x2 - комплексно-сопряжённые
Re x1 = - 4,0000; Im x1 = 10,000;
Re x2 = - 4,0000; Im x2 = - 10,000.
Дано алгебраическое уравнение пятой степени
(x**5) + 18* (x**4) - 96* (x**3) - 1198* (x**2) - 1425*x + 2700 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC5 = 4,8559.
Коэффициент выбора формулы расчета I1 = 3.
I2 = 1.
Порядковый номер преобразования J = 2.
Корень x5 - действительный
x5 = 1,0000.
Корни x3, x4 - действительные
x3 = 9,0000; x4 = - 20,000;
Корни x1, x2 - действительные
x1 = - 3,0000; x2 = - 5,0000.
Дано алгебраическое уравнение пятой степени
(x**5) + 24* (x**4) + 19* (x**3) - 1646* (x**2) - 9222*x - 14040 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC5 = - 6,7526.
Коэффициент выбора формулы расчета I1 = 1.
I2 = 5
Порядковый номер преобразования J = 3
Корень x5 - действительный
x5 = - 20,000.
Корни x3, x4 - действительные
x3 = - 3,0000; x4 = 9,0000;
Корни x1, x2 - комплексно-сопряжённые
Re x1 = - 5,0000; Im x1 = 1,0000;
Re x2 = - 5,0000; Im x2 = - 1,0000.
Дано алгебраическое уравнение пятой степени
(x**5) + 30* (x**4) + 309* (x**3) + 2510* (x**2) + 6150*x - 9000 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC5 = - 6,1780.
Коэффициент выбора формулы расчета I1 = 3.
I2 = 2
Порядковый номер преобразования J = 1
Корень x5 - действительный
x5 = 1,0000;
Корни x3, x4 - действительные
x3 = - 5,0000; x4 = - 20,000;
Корни x1, x2 - комплексно-сопряжённые
Re x1 = - 3,0000; Im x1 = 9,0000;
Re x2 = - 3,0000; Im x2 = - 9,0000.
Дано алгебраическое уравнение пятой степени
(x**5) + 36* (x**4) + 496* (x**3) + 4576* (x**2) + 23460*x + 46800 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC5 = 8,5911.
Коэффициент выбора формулы расчета I1 = 2.
I2 = 5.
Порядковый номер преобразования J = 3.
Корень x5 - действительный
x5 = - 20,000;
Корни x3, x4 - комплексно-сопряжённые
Re x3 = - 3,0000; Im x3 = 9,0000;
Re x4 = - 3,0000; Im x4 = 9,0000;
Корни x1, x2 - комплексно-сопряжённые
Re x1 = - 5,0000; Im x1 = 1,0001;
Re x2 = - 5,0000; Im x2 = - 1,0001.
Дано алгебраическое уравнение шестой степени
(x**6) + 1* (x**5) - 261* (x**4) + 251* (x**3) + 14708* (x**2) - 13260*x - 79200 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC6 = 6,5532.
Коэффициент выбора формулы расчета I1 = 3.
I2 = 5.
Порядковый номер преобразования J = 3.
Корни x5, x6 - действительные
x5 = 3,0000; x6 = - 2,0000;
Корни x3, x4 - действительные
x3 = 11,000; x4 = - 15,000;
Корни x1, x2 - действительные
x1 = 10,000; x2 = - 8,0000.
Дано алгебраическое уравнение шестой степени
(x**6) + 13* (x**5) - 29* (x**4) - 660* (x**3) - 17300* (x**2) - 79944*x + 411840 = 0.
Решение:
Степень точности EPS = 0,00001.
Нормирующий коэффициент для исходного уравнения RC6 = 8,6256.
Коэффициент выбора формулы расчета I1 = 3.
I2 = 1.
Порядковый номер преобразования J = 2.
Корни x5, x6 - действительные
x5 = - 8,0000; x6 = 3,0000;
Корни x3, x4 - комплексно-сопряжённые
Re x3 = - 2,0000; Im x3 = 10,000;
Re x4 = - 2,0000; Im x4 = - 10,000;
Корни x1, x2 - действительные
x1 = - 15,000; x2 = 11,000.
Похожие работы
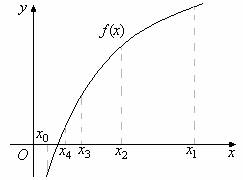
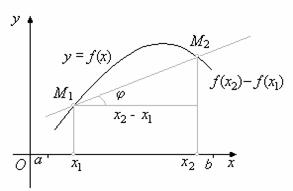
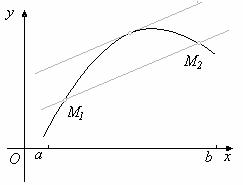
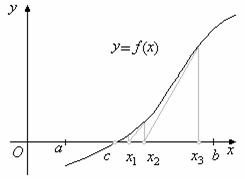
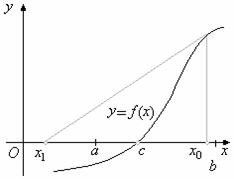
... - в методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики ...
... «проявляется» лишь в процессе преобразований. Очевидность и «завуалированность» новой переменной мы рассмотрим на конкретных примерах во второй главе данной работы. 2. Возможности применения метода замены неизвестного при решении алгебраических уравнений В этой главе выявим возможности применения метода замены неизвестного при решении алгебраических уравнений в стандартных и нестандартных ...
... математики тригонометрической подстановки и проверка эффективности разработанной методики преподавания. Этапы работы: 1. Разработка факультативного курса на тему: «Применение тригонометрической подстановки для решения алгебраических задач» с учащимися классов с углубленным изучением математики. 2. Проведение разработанного факультативного курса. 3. Проведение диагностирующей контрольной ...
... численных методов (при решении реальных, а не учебных задач!) предполагает использование компьютеров с достаточным быстродействием. Использование для численного решения дифференциальных уравнений компьютерного пакета MathCAD предполагает знание алгоритма работы численных методов для разумного их применения (знание границ применимости, оценки точности, затрат компьютерных ресурсов и др.). Дело в ...

0 комментариев