Особенности
контроля в
учебной деятельности
младших школьников
Критерии
и уровни сформированности
действия контроля
Выводы по
главе
Особенности
формирования
действия контроля
в процессе
работы над
вычислительными
приёмами и
навыками
Выводы по
главе
Обучающий
эксперимент
с целью развития
действия контроля
в процессе
работы над
вычислительными
приёмами и
навыками
Анализ
результатов
обучающего
эксперимента
Выводы по
главе
Навигация
Обучающий эксперимент с целью развития действия контроля в процессе работы над вычислительными приёмами и навыками
Формирование действия контроля в процессе работы над вычислительными приемами и навыками у младших школьников
107907
знаков
22
таблицы
8
изображений
3.2 Обучающий эксперимент с целью развития действия контроля в процессе работы над вычислительными приёмами и навыками
Анализ психолого – педагогической и методической литературы по проблеме исследования путей и условий развития действия контроля в процессе работы над вычислительными приемами навыками показал, что данная проблема не достаточно исследована на практике. Кроме этого, анализ учебных программ свидетельствует о том, что в традиционной программе уделяется меньше внимания развитию действия контроля, чем в развивающих системах. Таким образом, на основании изученной литературы и выявленного уровня сформированности действия контроля у учащихся школы№ 25 г. Иркутска в классе 3 «Д», нами были выделены следующие задачи: 1) разработать программу экспериментальной работы, направленной на развитие действия контроля в процессе работы над вычислительными приемами и навыками; 2) апробировать программу экспериментальной работы на базе школы №25 г. Иркутска в классе 3 «Д». Содержание программы базируется на следующих принципах:
создание благоприятных условий, способствующих развитию действия контроля.
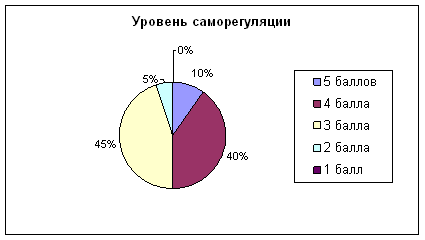
индивидуальный уровень сформированности действия контроля.
умение контролировать как действия других людей, так и свои собственные.
умение контролировать весь процесс осуществления действия.
Нами была составлена экспериментальная программа в виде таблицы, где представлены этапы исследования, задачи, виды работ, направленные на формирование действия контроля в процессе овладения вычислительными приемами и навыками. (таблица №7 , приложение 7 )
Рассмотрим более детально этапы экспериментальной работы:
1 этап – подготовительный. Включает следующие задачи:
формировать потребность в осуществлении действия контроля.
способствовать осознанию действия контроля.
актуализировать знания о месте действия контроля в учебной деятельности.
обогатить знания о действии контроля.
Для осуществления перечисленных задач была проведена беседа с учащимися о важности действия контроля, о том, зачем нужно контролировать свои действия. Для того, чтобы ученик пришел к необходимости делать проверку, детям предлагалось найти значение выражения и сверить конечный результат с ответом, записанным на доске (неверным).
В процессе работы перед выполнением каждого вычисления была организована установка на контроль.
Ученикам предлагались деформированные выражения, а также задания, выполнить которые было невозможно, не осуществив контроль: выражения, выписанные на доску, были составлены так, что ответ каждого выражения являлся началом какого – то другого.
2 этап – основной. Задача – учить осуществлять проверку по готовому алгоритму; развивать умение учащихся обнаруживать ошибки: в действиях своих товарищей, учителя, собственных, в результате действия, в процессе действия.
С целью приучения контролировать не только собственные действия, но и действия своих товарищей, учителя, дети выполняли вычисление, после чего им предлагалось обменяться тетрадями и проверить вычисления товарища.
В своей работе мы использовали задания, направленные на развитие умения учащихся обнаруживать ошибки, умение объяснять их, выявлять причины их возникновения, такие как: а) решение учителя с преднамеренной ошибкой, б) детям предлагалось найти ошибку и подумать, что привело к появлению ошибки, в) учащиеся задавали такой вопрос отвечающему у доски, чтобы он нашел, исправил и объяснил ошибку. Наша работа была направлена на развитие у детей умение задавать уточняющие вопросы, доказательно рассуждать.
3 этап – заключительный. Задача которого – учить детей самостоятельно разрабатывать алгоритм контрольного действия, ставить учебную задачу на основе контроля.
Мы сочли необходимым показать детям, что существует контроль не только по результату, но и контроль, который охватывает весь процесс осуществления действия (пооперационный). Взаимоконтроль по процессу повышает КПД практической работы, так как почти исключает ошибки в тетради учащихся, формирует речь учащихся, дает возможность слабым учащимся лучше разобраться в изучаемом материале
В ходе работы нам было важно учить детей осуществлять рефлексивный контроль: реконструировать способ действия товарища, учителя, приведший к ошибке.
На данном этапе мы использовали задания, направленные на разработку алгоритма контрольного действия. Работа была реализована не полностью, так как требует больше времени для ее осуществления.
Апробацию программы мы проиллюстрируем на примере некоторых уроков.
Фрагмент урока№1
Задачи по развитию действия контроля:
Формировать потребность в осуществлении действия контроля;
Развивать умение осуществлять контроль по результату;
Развивать умение контролировать действия товарища, собственные действия;
Развивать умение доказательно рассуждать;
| Экспериментальные комментарии | Ход урока |
| 2 этап – Повторение вид работы – устный счет Задача для учителя: проверить осознанность, прочность вычислительных приемов относительно устных приемов сложения, деления. Задача для учащихся: Ребята, сегодня мы продолжим говорить о значении действия контроля, выполним задания, направленные на умение складывать числа, оканчивающиеся на 0, повторим устные приемы деления; | |
Умение осуществлять контроль по результатам (сопоставлять ответы) Умение осуществлять контроль по результату. Развиваем умение обнаруживать ошибки в решениях товарищей. Это помогает в развитии умения находить ошибки в собственных действиях. Развиваем умение доказательно рассуждать. | Уч. Зад. №1. Практич. Задание: Найдите значения выражений, сопоставив результаты и буквы на цветках, и вы узнаете имя мультипликационного героя, который пришел к нам на урок. Содержание: 270:270=…; 260:130=…; 930:310=…; 420:105=…; 600:120=…; 666:111=…; 280:40=…; 560:70=…;
А Т А К П Е Ш С 5 2 8 7 4 3 6 1 Кто пришел в гости? (Степашка). Как вы это узнали? (Сопоставили результаты выражений и цифры на цветках). Молодцы! Вы очень сообразительны. Мы проверили значения выражений с помощью ответов. Уч. Зад. №2. Ребята, кто знает, какая птица может ходить по дну водоема? Чтобы ответить на этот вопрос, выполните вычисление: Содержание: 250+150+30+120+250=…; Ответы: воробей = 850; оляпка= 800; сорока=700; К нам в гости пришел Незнайка и он утверждает, что по дну водоема может ходить воробей. Вы с ним согласны? Докажите, что Незнайка не прав. Как вы сумели доказать свою правоту? (Выполнили проверку). Как вы считаете, без проверки вы смогли бы доказать свое мнение? Для чего необходима проверка? Итог: Мы не сможем доказать, что решение верно, не будем уверены в достоверности результата, если не выполним проверку, не проконтролируем свои действия. |
Фрагмент урока №2
Задачи по развитию действия контроля:
развивать умение осуществлять парный контроль.
Развивать умение задавать уточняющие вопросы
Развивать умение обнаруживать ошибки в решениях товарищей
Развивать умение осуществлять рефлексивный контроль: реконструировать способ действий, приведший к ошибке.
Развивать умение осуществлять контроль по результату.
| Экспериментальные комментарии. | Ход урока |
Развиваем умение осуществлять парный контроль. Развиваем умение обнаруживать ошибки. Развиваем умение осуществлять рефлексивный контроль: реконструировать решения, приведшие к ошибке. Развиваем умение доказательно рассуждать. Развиваем умение развивать контроль по результату, контролировать действие своих товарищей. | 2 этап. Повторение вид работы – устный счет Задача для учителя: проверить устные приемы умножения и деления на однозначные, круглые двузначные и трехзначные числа. Задача для учащихся: Мы повторим устные приемы умножения и деления, продолжим учиться обнаруживать ошибки в вычислениях. Это умение поможет нам не допускать ошибки и вовремя замечать их. Уч. Зад.№1 . Ребята, Чебурашка и Шапокляк прислали нам несколько выражений. Но в конверте все выражения перепутались и теперь мы не знаем, где решения Чебурашки, а где «ловушки» Шапокляк. Поэтому мы не можем быть уверены, что все решения верны, так как Шапокляк любит делать мелкие пакости. Наша задача обсудить выражения и их значения и обнаружить ошибки, если таковые имеются. Содержание: 560:70=80; 360:9=50; 490:90=90; 70 * 9=6500; 30 * 800=2700; 500 * 70=35000; Работаем в парах. Вам необходимо просмотреть все действия, обнаружить ошибки, объяснить их своему соседу и, доказательно рассуждая исправить их. Итак, сколько вычислений прислал Чебурашка? (Одно). Вы смогли обнаружить и устранить «ловушки» Шапокляк? Молодцы! Это поможет нам не допускать ошибки и быть более внимательными. Уч. Зад. №2 Практич. Задание: Найдите значения выражений: Содержание: 7080:20=…; 1020:20=…; 630:30=…; 3050:50=…; 2800:40=…; Ответы для самоконтроля: 308;354;402; 413; 423;484;554; Для того чтобы проверить себя, суммируйте ответы 1 и 2 выражений. Если сумма указана в ответах для самоконтроля, то значения верны, переходите к следующему вычислению. Саша назовет значения 1 и 2 выражений, их сумму, а вы внимательно слушайте и исправляйте по необходимости своего товарища. Итак, мы нашли верные значения, поучились контролировать себя, своих товарищей, исправлять, доказательно рассуждая. |
Фрагмент урока№3
Задачи по развитию действия контроля:
Развивать умение разрабатывать алгоритм контрольного действия.
Развивать умение осуществлять пооперационный контроль.
Развивать умение обнаруживать ошибку в ходе вычислений.
| Экспериментальные комментарии | Ход урока |
Операционный контроль Умение обнаруживать ошибки в вычислениях, объяснять их. Умение разрабатывать алгоритм контрольного действия. Умение контролировать действия своих товарищей. | 3 этап: Закрепление изученного материала. Вид работы – выполнение вычисления Задача для учителя: закреплять умение выполнять письменное деление многозначных чисел, продолжить учить обнаруживать ошибки в вычислениях; Задача для учащихся: Мы продолжим выполнять письменное деление многозначных чисел, поучимся обнаруживать ошибки, объяснять их. Практич. Задача: Злая колдунья Гогера отправила к нам своих злых слуг обезьян. Они принесли выражение, в котором, возможно, есть ошибка. Колдунья уверена, что мы ошибку не найдем и превратимся в глупых учеников. Что нам поможет найти ошибку? (Проверка). Правильно, мы должны поучиться проверять не только результат решения, но и весь процесс выполнения вычисления. Нам необходимо составить алгоритм проверки, с помощью которого мы найдем ошибку. Мы уже составляли подобные алгоритмы, так что думаю, мы справимся с этим. Что нам было важно контролировать в процессе выполнения вычислений? На что нужно обратить внимание? (1. Чтобы определить, правильно мы выделили 1 неполное делимое, нам необходимо отсчитать такое количество цифр в делимом, сколько в делителе. Если число, получившееся в делимом, меньше делителя, значит 1 неполное делимое будет больше делителя на одну цифру. Если число, получившееся в делимом, больше делителя, следовательно, оно является 1 неполным делителем. 2. Чтобы определит, верно ли мы подобрали количество цифр в частном, важно найти 1 неполное делимое и посчитать количество оставшихся разрядов. 3. Чтобы определить, правильно ли подобрана цифра в частном, нужно ее умножить на делитель. Получившееся число должно быть не больше делимого, а остаток меньше делителя. Ваня попробует порассуждать. Остальные внимательно слушают и контролируют ход мыслей своего товарища. Итак, мы справились с заданием, составили алгоритм проверки деления многозначных чисел, который помог нам найти ошибку. Руководствуясь этим алгоритмом, вы сможете выполнять деление чисел без ошибок. |
Похожие работы
... , внесение усовершенствований. Проанализировав психолого-педагогическую и методическую литературу, можно сделать вывод, что эффективность формирования навыка самоконтроля у младших школьников достигается в результате использования таких методов и приемов (сверка с написанным образцом; взаимопроверка с товарищем; коллективное выполнение задания и коллективная проверка; сочетание коллективной и ...
... Оно и определило формулировку проблемы: каковы условия продуктивного формирования УД младших школьников при обучении математике с применением персональных компьютеров? Целью исследования является выявление особенностей формирования учебной деятельности младших школьников при обучении математике с применением ПК. Объектом исследования выступает методическая система обучения младших школьников ...
... современными представлениями о нем, методами изучения творчества, качествами творческой личности, их системой, чтобы иметь возможность формировать такие качества у школьников начальных классов. Раздел 2. Методическая система формирования творческой личности младшего школьника средствами математики 2.1. Методика формирования творческой личности при обучении математике Речь должна идти о ...
... и суммы на число. Рассмотрение этих двух правил диктуется методическими соображениями. Глава II. Исследовательская работа по изучению формирования понятия свойств арифметических действий у младших школьников 2.1 Изучение арифметических действий и их свойств в различных системах обучения В программе Моро М.И. уделяется значительное внимание формированию у учащихся осознанных и прочных, ...
0 комментариев