Навигация
Выводы по главе
3.4. Выводы по главе.
Проведенный эксперимент позволяет сделать следующие выводы.
Формирование действия контроля предполагает развитие не только умение соотносить объект контроля с образцом, но и умение самостоятельно выбирать или конструировать такие образцы- критерии успешности выполнения тех или иных действий, критерии достижения той или иной цели. Приемам действия контроля необходимо специально учить.
Развитие умения предвидеть результаты своих действий, отдавая отчет в правильности их выполнения, сопоставляя выполняемые действия с определенным образцом, позволяет не только исправлять ошибки, но и предотвращать возможность их появления.
У учащихся следует формировать умение проверять не только конечный результат выполненной работы, но и весь процесс ее выполнения. Формирование полноценного действия контроля возможно только на основе пооперационного контроля, так как он предполагает выяснение тех операций, способов, действий, с помощью которых получен результат.
В связи с тем, что выполнение вычислительных приемов представляет собой мыслительный процесс и является сложным умственным действием, имеющим свое операционное содержание, то овладение вычислительным приемом и умение осуществлять контроль за его выполнением должно осуществляться одновременно в процессе обучения при правильной организации деятельности учащихся.
Такой подход к формированию действия контроля в процессе работы над вычислительными приемами и навыками позволит учащимся избежать трудности в вычислениях, так как ими будут усвоены все специфические особенности вычислительных приемов.
Заключение
Экспериментальная работа дает возможность сформулировать теоретические выводы и практические рекомендации по формированию действия контроля в процессе работы над вычислительными приемами и навыками у младших школьников.
Действие контроля является необходимым компонентом учебной деятельности.
Сущность действия контроля заключена в обязательном сопоставлении, соотнесении действий с «образцом», - эталоном действия.
Следовательно, целесообразно обучать детей не только пользоваться готовым эталоном для осуществления действия контроля, но и самостоятельно разрабатывать эталон контрольного действия.
Процесс выполнения вычислительного приема и осознанное его контролирование должны быть двумя сторонами единого процесса овладения вычислительным приемом, так как при развитии действия контроля на уроках математики, совершенствуется умение осознанно выполнять вычислительные приемы.
Необходимо обучать учащихся не только общему способу контроля процесса овладения вычислительным приемом, но и умению переносить этот способ на конкретные виды вычислительных приемов.
В предположении нами были выделены условия формирования действия контроля в процессе работы над вычислительными приемами и навыками. Для создания условий мы разработали программу экспериментальной работы, направленную на развитие действия контроля у младших школьников.
Основываясь на программу, мы выделили этапы экспериментальной работы.
Первый этап направлен на стимулирование потребности в осуществлении действия контроля.
Второй этап связан с умением осуществлять проверку по готовому плану, обнаруживать ошибки (в действиях учителя, товарищей, собственных; в результате действия, в ходе действия, в способе действия).
Результаты исследования показали, что с возрастанием уровня сформированности действия контроля усиливается познавательный интерес к уроку математики, совершенствуются вычислительные навыки.
Предположение, выдвинутое в начале исследования, в основном подтвердилось: формирование действия контроля, при соблюдении следующих условий:
выделение структурных особенностей действия контроля для отдельных вычислительных приемов;
использование в процессе обучения системы заданий, направленной на усвоение алгоритмов контрольных действий учащимися;
постановка перед учащимися задачи на контроль,
привело к качественному изменению показателей сформированности действия контроля у младших школьников.
Следовательно, мы можем утверждать, что выделенные нами условия формирования действия контроля в процессе работы над вычислительными приемами и навыками оказались эффективными.
Таким образом, развитие действия контроля в процессе работы над вычислительными приемами и навыками при соблюдении данных условий говорит о том, что разработанная программа экспериментального обучения является эффективным средством формирования структурных компонентов учебной деятельности младших школьников.
Литература
Абрамова Г. С. Возрастная психология. Учебное пособие для студент. вузов.- М.: Академия, 1997 – 638 с.
Аргинская И. И. Математика 3 класс. – Самара, « Корпорация» Федоров», 1997 – 88 с.
Бабанский Ю. К. Оптимизация процесса обучения. Общедидактический аспект. – М.: Педагогика, 1977 – 254 с.
Берцфаи Л. В.. Специфика учебного действия контроля //Вопросы психологии – 1987, - №4 – с. 55 - 60
Берцфаи Л. В., Поливанова К.Н. Диагностика действия контроля // Диагностика учебной деятельности и интеллектуального развития детей. – М., 1981 – с. 29 - 40
Берцфаи Л. В., Романко В. Г. Исследование особенностей рефлексивного контроля. Сообщение 1 // Новые исследования в психологии – 1981, - №2 – с. 68 – 72
Бадма – Гаряева М. В. Развитие вычислительных навыков у учащихся 1 класса // Начальная школа – 1999 - №11 – с.21 – 23
Бантова М. А. Система формирования вычислительных навыков // Начальная школа – 1993 - №11 – с. 38 - 43
Батий Ю. Ю. Самоконтроль учащихся при выполнении заданий // Начальная школа – 1979 - №4 – с.41 – 43
Бахир В. К. Развивающее обучение // Начальная школа – 1997 - №5 – с. 26 – 31
Воронцов А. Б. Некоторые подходы к вопросу контроля и оценки учебной деятельности учащихся // Начальная школа – 1999 - №7 – с.61 – 71
Давыдов В. В. Проблемы развивающего обучения: опыт теоретического и экспериментального психологического исследования. – М.: Педагогика, 1986 – 239 с.
Давыдов В. В. Содержание и строение учебной деятельности школьников. – М., 1978 – 321 с.
Давыдов В.В. Теория развивающего обучения. – М.: ИНТОР, 1996 – 544 с.
Давыдов В. В. Что такое учебная деятельность // Начальная школа – 1999 - №7 – с. 12 – 18
Елагина Л.Н. Самоконтроль и самооценка в процессе обучения математике // Начальная школа – 1082 - №8 – с. 65 – 67
Емельяненко М. В. Система развивающих заданий по теме « Умножение многозначного числа на однозначное» // Начальная школа – 1996 - №12 – с. 47 – 50
Захарова А.В. Развитие контроля и оценки в процессе формирования учебной деятельности//Формирование учебной деятельности школьников. – М., 1982 – 234 с.
Зимняя И. А. Педагогическая психология. – Ростов на Дону: Феникс, 1997 – 476 с.
Камышева И.Н. Пособие для самоконтроля на уроках математики // Начальная школа – 1988 - №10 – с.36 - 37
Леонтьев Л. Н. Деятельность. Сознание. Личность – 2 – е изд. – М., 1977 – 364 с.
Максимова Т.П. Влияние формы кооперации младших школьников на развитие контрольно - оценочных действий.// Развитие мотивационно – познавательной сферы младшего школьника в условиях учебной деятельности. – Волгоград, 1985 – 276 с.
Мальцева К.П. Самоконтроль в учебной работе младшего школьника. – М., 1962 – 389 с.
Мор Г.Я. Формирование навыков самоконтроля и взаимоконтроля у учащихся //Начальная школа – 1993 - №11 – с.38 – 43
Никифоров Г.С. Самоконтроль человека. – М., - с. 90 – 94
Особенности психического развития детей 6 – 7 летнего возраста /Под ред. Д.Б.Эльконина, А.Л.Венгера – М.: Педагогика, 1988 – 137 с.
Петровский В.А., Черепанова Е.М. Индивидуальные особенности самоконтроля при организации внимания//Вопросы психологии. – 1987 - №5 – с.48 – 51
Познавательные процессы и способности в обучении / Под ред. В.Д. Шадрикова. – М.: Просвещение, 1996 – 168 с.
Поливанова К.Н. Психологические формирования действия контроля в учебной деятельности. // Новые исследования в психологии. – 1983, - №1 – с. 65 – 68
Психологическое развитие младших школьников/ Под ред. В.В. Давыдова. – М.: Педагогика, 1990 – с.22—103
Реализация межпредметных и внутрипредметных связей в обучении и воспитании младших школьников: Межвузовский сборник научных трудов. – Л., 1984 – 132 с.
Репкин В.В. Формирование учебной деятельности в младшем школьном возрасте//Начальная школа – 1999 - №7 – с.19 – 24
Репкина Г.В., Заика Е.В. Оценка уровня сформированности учебной деятельности. Томск: Пеленг, 1993 – 62 с.
Романко В.Г. Особенности рефлексивного контроля как учебного действия//Новые исследования в психологии – 1985, - №1 – с.65 – 71
Самоконтроль младших школьников в процессе решения арифметических задач: Методические рекомендации / Сост. Г.М. Соснина. – Иркутск, 1983 – 34с.
Талызина Н.Ф. Педагогическая психология – М.: Академия, 1998 – 497 с.
Талызина Н.Ф. Формирование познавательной деятельности младших школьников. – М.: Просвещение, 1988 – 374 с.
Фридман Л.М., Кулагина М.Ю. Психологический справочник учителя. – М.: Просвещение, 1991 – 287 с.
Эльконин Д.Б. Избранные психологические труды. – М., 1995, - 342 с.
Эльконин Д.Б. К проблеме периодизации психического развития в детском возрасте // Вопросы психологии – 1971, - №4 – с. 57 – 61.
Приложение 1
| Вопросы Фамилия ученика | 1. Какие задания тебе нравится выполнять по математике | 2. Любишь ли ты выполнять вычисления | 3. Какие ошибки чаще всего допускаешь в вычислениях | 4. Можешь ли самостоятельно найти и исправить ошибки в допущенных вычислениях | 5. Нравится ли открывать новые способы вычисления | 6. Всегда ли делаешь проверку вычисления |
| Бычковский | Вычисления | Да | Никаких | Да | Нет | Нет |
| Ильин | Вычисления | Да | В значении | Иногда | Да | Иногда |
| Исаков | Умножение | Да | Переход через десяток | Да | Да | Нет |
| Грицюк | Сложение | Нет | Обычные | Нет | Иногда | Да |
| Андреев | Задачи | Да | Умножение | Нет | Да | Нет |
| Гичева | Задачи | Да | Значение | Иногда | Нет | Да |
| Козинец | Уравнения | Да | Никаких | Да | Иногда | Да |
| Неверова | Выражения на умножение | Да | Никаких | Иногда | Да | Иногда |
| Оборин | Вычисление | Да | Не знаю | Да | Не знаю | Нет |
| Леонов | Задачи | Да | Не знаю | Нет | Нет | Нет |
| Наумов | Вычисление | Да | Деление | Иногда | Да | Нет |
| Манькова | Вычисление | Да | Никаких | Нет | Иногда | Нет |
| Клещев | Примеры на сложение | Да | Никаких | Да | Да | Да |
| Жвакин | Примеры на вычитание | Да | В табличных случаях | Иногда | Да | Нет |
| Шолхонов | Сложные задачи | Да | Деление | Да | Иногда | Не всегда |
| Топорков | Примеры на сложение | Нет | Никаких | Нет | Нет | Иногда |
| Фролов | уравнения | Да | Не знаю | Иногда | Да | Да |
| Солонин | Задачи | Да | Значение | Иногда | Не всегда | Иногда |
| Подкова | Вычисление | Да | Переход через десяток | Нет | Да | Да |
| Шестопалова | Задачи | Да | Деление | Иногда | Иногда | Да |
| Ольховский | Никакие | Нет | В табличных случаях | Нет | Нет | Нет |
| Подварков | Лёгкие задания | Да | Деление | Иногда | Да | Нет |
| Торгашин | Выражения на умножение | Да | Переход через десяток | Да | Иногда | Да |
Приложение 2
Таблица 2
Выделение исходного уровня сформированности действия контроля в экспериментальном классе
| Критерии сформированности действия контроля Фамилия ученика | Осуществление контроля по результату | Умение обнаруживать ошибку учителя | Умение осуществлять пооперационный контроль | Умение реконструировать способ действия |
| Андреев | - | - | - | - |
| Бычковский | + | + | + | - |
| Гичева | + | - | + | + |
| Грицюк | - | - | - | - |
| Жвакин | + | + | + | + |
| Ильин | - | + | + | - |
| Исаков | + | + | + | - |
| Клещев | + | + | + | - |
| Козинец | + | + | + | + |
| Леонов | + | + | + | - |
| Манькова | + | - | - | - |
| Наумов | + | + | - | - |
| Неверова | + | + | + | + |
| Оборин | - | + | - | - |
| Ольховский | - | + | - | - |
| Подварков | - | - | + | - |
| Подкова | + | + | + | - |
| Солонин | + | + | - | - |
| Топорков | - | + | - | - |
| Торгашин | + | - | + | - |
| Фролов | - | + | + | - |
| Шестопалова | + | + | + | - |
| Шолхонов | + | + | + | - |
Приложение 3
Таблица 3
Уровни сформированности действия контроля в экспериментальном классе
| Фамилия Имя ученика | Уровень сформированности действия контроля |
| Андреев Саша | 1 |
| Бычковский Витя | 3 |
| Гичева Катя | 2 |
| Грицюк Альберт | 1 |
| Жвакин Сергей | 4 |
| Ильин Толя | 2 |
| Исаков Валентин | 3 |
| Клещев Артём | 4 |
| Козинец Даша | 3 |
| Леонов Иван | 3 |
| Манькова Катя | 2 |
| Наумов Артём | 2 |
| Неверова Маша | 4 |
| Оборин Сергей | 2 |
| Ольховский Эрик | 2 |
| Подварков Паша | 2 |
| Подкова Юля | 3 |
| Солонин Егор | 2 |
| Топорков Юра | 2 |
| Торгашин Влад | 2 |
| Фролов Женя | 2 |
| Шестопалова Кристина | 3 |
| Шолхонов Дима | 3 |
Приложение 4
Таблица 4
Уровни сформированности действия контроля в контрольном классе
| Фамилия ученика | Уровень сформированности действия контроля |
| Антонов | 3 |
| Амосов | 2 |
| Барабанов | 3 |
| Быков | 3 |
| Барковская | 2 |
| Вершилло | 3 |
| Дроздова | 2 |
| Дробышева | 2 |
| Игнатьев | 3 |
| Купряков | 1 |
| Краснов | 3 |
| Лопатина | 3 |
| Москвитин | 2 |
| Муравьёва | 3 |
| Малинский | 2 |
| Орданов | 4 |
| Румынин | 2 |
| Родникова | 5 |
| Светлакова | 2 |
| Соболев | 2 |
| Трухин | 4 |
| Яблонов | 2 |
Приложение 5
Таблица 5
Уровни сформированности вычислительного навыка в экспериментальном классе
| Фамилия Имя ученика | Уровень сформированности вычислительного навыка: | ||
| Правильность | Осознанность | Прочность | |
| Андреев Саша | 1 | 1 | 1 |
| Бычковский Витя | 2 | 2 | 3 |
| Гичева Катя | 2 | 2 | 2 |
| Грицюк Альберт | 1 | 1 | 1 |
| Жвакин Сергей | 3 | 2 | 2 |
| Ильин Толя | 2 | 2 | 1 |
| Исаков Валентин | 2 | 2 | 3 |
| Клещев Артём | 2 | 2 | 2 |
| Козинец Даша | 2 | 2 | 3 |
| Леонов Иван | 2 | 1 | 2 |
| Манькова Катя | 1 | 1 | 2 |
| Наумов Артём | 1 | 1 | 2 |
| Неверова Маша | 3 | 2 | 3 |
| Оборин Сергей | 1 | 1 | 2 |
| Ольховский Эрик | 2 | 1 | 1 |
| Подварков Паша | 1 | 2 | 2 |
| Подкова Юля | 2 | 3 | 3 |
| Солонин Егор | 2 | 2 | 2 |
| Топорков Юра | 1 | 1 | 1 |
| Торгашин Влад | 2 | 2 | 1 |
| Фролов Женя | 2 | 3 | 2 |
| Шестопалова Кристина | 2 | 2 | 3 |
| Шолхонов Дима | 2 | 2 | 2 |
Приложение 6
Таблица 6
Уровни сформированности вычислительного навыка в контрольном классе
| Фамилия Имя ученика | Уровень сформированности вычислительного навыка: | ||
| Правильность | Осознанность | Прочность | |
| Антонов | 2 | 2 | 2 |
| Амосов | 1 | 1 | 2 |
| Барабанов | 2 | 1 | 2 |
| Быков | 2 | 2 | 3 |
| Барковская | 1 | 2 | 1 |
| Вершилло | 2 | 2 | 3 |
| Дроздова | 1 | 2 | 2 |
| Дробышева | 2 | 2 | 2 |
| Игнатьев | 2 | 2 | 2 |
| Купряков | 1 | 1 | 1 |
| Краснов | 2 | 2 | 2 |
| Лопатина | 2 | 2 | 2 |
| Москвитин | 1 | 1 | 2 |
| Муравьёва | 3 | 2 | 2 |
| Малинский | 2 | 2 | 1 |
| Орданов | 3 | 3 | 3 |
| Румынин | 1 | 1 | 2 |
| Родникова | 3 | 3 | 3 |
| Светлакова | 2 | 2 | 2 |
| Соболев | 2 | 2 | 1 |
| Трухин | 3 | 3 | 3 |
| Яблонов | 2 | 2 | 2 |
Приложение 8
Таблица 8
| Критерии сформированности действия контроля Фамилия имя ученика | Умение осуществлять контроль по результату | Умение обнаруживать ошибку учителя | Умение объяснять ошибку | Умение осуществлять контроль по процессу | Умение осуществлять рефлексивный контроль: реконструировать способ действия |
| Андреев Саша | + | + | + | - | - |
| Бычковский Витя | + | + | + | + | + |
| Гичева Катя | + | + | + | + | - |
| Грицюк Альберт | + | + | - | + | + |
| Жвакин Сергей | + | + | + | + | + |
| Ильин Толя | + | + | + | + | + |
| Исаков Валентин | + | + | + | + | - |
| Клещев Артём | + | + | + | + | + |
| Козинец Даша | + | + | + | + | + |
| Леонов Иван | + | + | + | - | - |
| Манькова Катя | + | + | + | + | + |
| Наумов Артём | + | + | + | + | - |
| Неверова Маша | + | + | + | + | + |
| Оборин Сергей | + | + | + | + | + |
| Ольховский Эрик | + | - | - | - | - |
| Подварков Паша | + | + | + | + | + |
| Подкова Юля | + | + | + | + | + |
| Солонин Егор | + | + | + | + | + |
| Топорков Юра | + | + | - | + | + |
| Торгашин Влад | + | + | - | - | - |
| Фролов Женя | + | + | + | + | + |
| Шестопалова Кристина | + | + | + | + | + |
| Шолхонов Дима | + | + | + | + | + |
Приложение 9
Таблица 9
Сформированность действия контроля у учащихся экспериментального класса
| Фамилия Имя ученика | Уровень сформированности действия контроля |
| Андреев Саша | 2 |
| Бычковский Витя | 4 |
| Гичева Катя | 3 |
| Грицюк Альберт | 2 |
| Жвакин Сергей | 4 |
| Ильин Толя | 3 |
| Исаков Валентин | 4 |
| Клещев Артём | 4 |
| Козинец Даша | 4 |
| Леонов Иван | 3 |
| Манькова Катя | 3 |
| Наумов Артём | 3 |
| Неверова Маша | 5 |
| Оборин Сергей | 3 |
| Ольховский Эрик | 2 |
| Подварков Паша | 3 |
| Подкова Юля | 4 |
| Солонин Егор | 3 |
| Топорков Юра | 3 |
| Торгашин Влад | 2 |
| Фролов Женя | 4 |
| Шестопалова Кристина | 5 |
| Шолхонов Дима | 5 |
Приложение 7
Таблица 7
Программа экспериментальной работы
| Предмет усвоения | Этап усвоения | Задачи, по формированию действия контроля | Виды работ направленные на формирование действия контроля |
| учтные приёмы сложения чисел оканчивающихся на 0. устные приёмы деления на однозначное число. письменные приёмы деления на двузначное число. письменные приёмы сложения и вычитания многозначных чисел. устные приёмы умножения и деления чисел, оканчивающихся на ноль. | применение применение восприятие применение применение | Первый этап: формировать потребность в осуществлении действия контроля, осознание назначения контроля формировать контроль по результату | беседа с детьми о важности действия контроля перед решением примера детям даётся установка на контроль детям предлагается найти значение выражения, и сверить результат с ответом, записанным на доске (неверным). Появляется необходимость выполнять проверку предлагаются деформированные выражения, а так же задания, выполнить которые не возможно, не осуществив контроль: выражения, выписанные на доску составлены так что ответ каждого является началом какого либо другого. сравнение решения с правильным (с образцом) |
| письменные приёмы деления на двузначное число устные приёмы умножения и деления на однозначные, двузначные, трехзначные числа устные приёмы сложения многозначных чисел устные приёмы деления на однозначные числа | осмысление применение применение применение | Второй этап: учить осуществлять проверку по готовому алгоритму учить обнаруживать ошибки: а. В действиях товарищей б. В действиях учителя в. в собственных действиях г. в результате действия; учить объяснять ошибку учить определять причину появления ошибки. | дети решаю примеры, после чего им предлагается проверить решение по алгоритму ученики решают пример после чего им предлагается обменяться тетрадями и проверить решение своего товарища учитель предлагает детям решение с преднамеренной ошибкой самостоятельная проверка работ учащихся сравнение решения с правильным (с |
| учить задавать уточняющие вопросы учить высказывать свою точку зрения | образцом решения) детям предлагается найти ошибку и подумать, что привело к её появлению учащиеся задают такой вопрос отвечающему у доски, чтобы он нашёл, объяснил и исправил ошибку | ||
| письменные приёмы деления на двузначное число устные приёмы сложения и вычитания многозначных чисел письменные приёмы деления на двузначное число письменные приёмы деления многозначных чисел | закрепление применение закрепление закрепление | Третий этап: учить осуществлять пооперационный контроль учить самостоятельно ставить учебную задачу на основе контроля учить осуществлять рефлексивный контроль: реконструировать решение товарища, учителя учить разрабатывать алгоритм контрольного действия | а. дан алгоритм решения и выполненное решение (неверное), детям предлагается найти и исправить ошибки в решении руководствуясь алгоритмом б. поэлементный анализ ответа ученика. Вызванный к доске ученик отвечает с использованием алгоритма контроля. Остальные слушают, отмечая плюсы и минусы ответа ученика. Затем поднимают сигнальные карточки, кто не согласен по первому пункту алгоритма, по второму и т.д. в. поочерёдное рассуждение. Классу даётся выражение в несколько действий, в котором необходимо расставить их последовательность в соответствии с правилами. Учащиеся работают парами, попеременно объясняя друг другу ход решения выражения г. выражения выписанные на доску составлены так, что ответ каждого является началом какого-то другого пред решением примера ученик ставит задачу: при выполнении данного действия чему я должен научиться детям предлагается выражение, решённое разными способами (среди которых верные и неверные), необходимо их реконструировать детям предлагается решить пример. После решения составляется алгоритм проверки |
| Стр. | ||
| Введение | 3 | |
| 1. | Особенности контроля в учебной деятельности младших школьников | 6 |
| 1.1 | Сущность действия контроля, его особенности в младшем школьном возрасте и место в структуре учебной деятельности | 6 |
| 1.2 | Критерии и уровни сформированности действия контроля | 11 |
| 1.3 | Выводы по главе | 16 |
| 2. | Возможности формирования действия контроля в процессе работы над вычислительными навыками | 17 |
| 2.1 | Общая характеристика формирования вычислительных приёмов и навыков у младших школьников | 17 |
| 2.2 | Особенности формирования действия контроля в работе над вычислительными приёмами и навыками | 29 |
| 2.3 | Выводы по главе | 32 |
| 3. | Экспериментальная работа по формированию действия контроля в процессе работы над вычислительными приёмами и навыками | 33 |
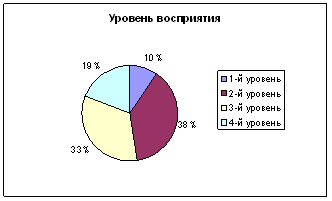
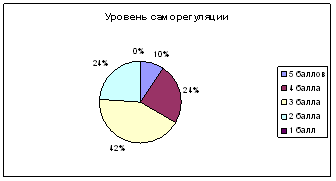
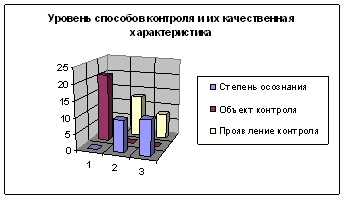
| 3.1 | Диагностика исходного уровня сформированности действия контроля на уроках математики | 33 |
| 3.2 | Обучающий эксперимент с целью развития действия контроля в процессе работы над вычислительными приёмами и навыками | 40 |
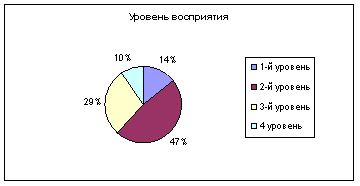
| 3.3 | Анализ результатов обучающего эксперимента | 44 |
| 3.4 | Выводы по главе | 49 |
| Заключение | 51 | |
| Литература | 53 | |
| Приложения |
Министерство образования Российской Федерации
Иркутский государственный педагогический университет
Кафедра методики начального образования
Факультет ПиМНО
Специальность «педагогика и методика начального образования»
Курс 5
Дипломная работа
Топорковой Надежды Геннадиевны
Формирование действия контроля в процессе работы над вычислительными приёмами и навыками у младших школьников
Научный руководитель:
Петрова М.А.
к.п.н; доцент.
Консультант: Кабаева Н.Н.
Ст. преподаватель.
Работа допущена
к защите______________________________
Зав. кафедрой__________________________
Дата представления_____________________
Дата возврата__________________________
Дата защиты___________________________
Оценка________________________________
ИРКУТСК
Похожие работы
... , внесение усовершенствований. Проанализировав психолого-педагогическую и методическую литературу, можно сделать вывод, что эффективность формирования навыка самоконтроля у младших школьников достигается в результате использования таких методов и приемов (сверка с написанным образцом; взаимопроверка с товарищем; коллективное выполнение задания и коллективная проверка; сочетание коллективной и ...
... Оно и определило формулировку проблемы: каковы условия продуктивного формирования УД младших школьников при обучении математике с применением персональных компьютеров? Целью исследования является выявление особенностей формирования учебной деятельности младших школьников при обучении математике с применением ПК. Объектом исследования выступает методическая система обучения младших школьников ...
... современными представлениями о нем, методами изучения творчества, качествами творческой личности, их системой, чтобы иметь возможность формировать такие качества у школьников начальных классов. Раздел 2. Методическая система формирования творческой личности младшего школьника средствами математики 2.1. Методика формирования творческой личности при обучении математике Речь должна идти о ...
... и суммы на число. Рассмотрение этих двух правил диктуется методическими соображениями. Глава II. Исследовательская работа по изучению формирования понятия свойств арифметических действий у младших школьников 2.1 Изучение арифметических действий и их свойств в различных системах обучения В программе Моро М.И. уделяется значительное внимание формированию у учащихся осознанных и прочных, ...


0 комментариев