Навигация
Расчет Э.Д.С. магнитной индукции во вторичной обмотке катушки индуктивности при протекании переменного во времени тока в первичной обмотке
2. Расчет Э.Д.С. магнитной индукции во вторичной обмотке катушки индуктивности при протекании переменного во времени тока в первичной обмотке.
Как известно, при протекании электрического тока по первичной обмотке катушки индуктивности внутри и вокруг витков катушки параллельно им образуется поле векторного потенциал A , в виде замкнутых колец. В этом поле размещена обмотка вторичной катушки. Как было показано раньше, на покоящиеся электрические заряды в таком поле действует сила равная:
![]()
Под действием силы со стороны изменяющегося во времени поля векторного потенциала A происходит смещение свободных электрических зарядов внутри провода вторичной обмотки катушки индуктивности, что приводит к разведению в нем разноименных зарядов и возникновению электрической напряженности E, препятствующей дальнейшему разведению электрических зарядов. Условием равновесия, согласно третьему закону Ньютона, является равенство нулю суммы магнитной (Fм) и электрической (Fэ) сил действующих на свободные заряды в проводнике. Запишем это условие:
![]()
откуда:
![]()
но т. к.
![]()
то внутри провода выполняется равенство:
![]()
И, следовательно, Э.Д.С. магнитной индукции равна:
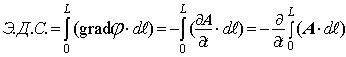
Но, полученный интеграл скалярного произведения векторного потенциала A на элемент провода вторичной обмотки катушки (dl), в случае цилиндрической катушки с числом витков вторичной обмотки равной "n", есть циркуляция вектора A и, согласно теореме Стокса, может быть преобразован следующим образом:
![]()
Где: ds - бесконечно малый элемент поверхности, охватывающий элементарный поток вектора магнитной индукции dФ нормальный к нему,
Ф - поток магнитной индукции.
Учитывая последнее соотношение можно получить окончательное выражение для Э.Д.С. магнитной индукции во вторичной обмотке с числом витков равным "n", возбуждаемым переменным во времени магнитным поле первичной обмоткой цилиндрической катушки индуктивности:
![]()
что хорошо известно, как закон индукции в переменном во времени магнитном поле.
Данная методика позволяет без каких либо допущений и дополнений, рассчитывать в векторной форме, различные электро- и радиотехнические устройства, опираясь на доступные физические модели процессов взаимодействия электрических зарядов с магнитным полем, основанные на фундаментальных законах классической механики.
Заключение Методология анализаВ данной работе в качестве критерия строгости исследуемых положений теории электромагнетизма, а также, при выводе системы уравнений магнитного поля, в основу анализа положено требование жесткого выполнения условия классического "триединства" результатов эксперимента, модели описываемого процесса и избранной формы математической записи .
При этом предполагалось что:
а) используемые при анализе результаты экспериментов не подлежат сомнению,
б) модели описываемых процессов строго согласованы с уже известными законами природы,
в) применение математического аппарата не предполагает деформацию каких.либо основополагающих принципов самого математического аппарата.
ВыводыРеализация в данной работе избранной методологии анализа позволила установить следующее:
а) в рамках теории электромагнетизма не существует никакой непротиворечивой физической модели распространения в пространстве световых и радиоволн, и природа их требует уточнения;
б) из проведенного рассмотрения классической методики получения выражения для Э.Д.С. электромагнитной индукции следует, что в рамках электродинамики Максвелла не существует непротиворечивой физической модели, способной дать описание процессов электромагнитной индукции, а предлагаемый при╖м искуствен и приводит к неустранимым противоречиям с экспериментом, третьим законом Ньютона и принципом причинности;
в) методы решения уравнений Максвелла предполагали широкое использование неоднозначностей в определении векторных полей и их потенциалов, якобы существующих в классической теории поля, что приводило к неограниченному "размножению" калибровочных соотношений, в корне противоречащих основным положениям классической теории поля и затрудняющих использование системы уравнений электродинамики в практической деятельности;
г) введенное Максвеллом в обращение вихревое электрическое поле породило неустранимые противоречия физических моделей процессов распространения электрического и магнитного полей и их взаимодействия с привнесенными физическими объектами, с экспериментальными результатами, математическим аппаратом теории поля, третьим законом Ньютона и принципом причинности,
д) различия между электрическим и магнитным полями в классическом случае фундаментальны:
1) электрическое поле имеет строго градиентный характер, т.е.:
![]()
![]()
2) магнитное поле полностью описывается с помощью векторного магнитного потенциала A и имеет строго вихревой характер, т.е.:
е) теория электромагнетизма, иначе называемая электродинамикой Максвелла, содержит в себе для описания электрического поля только систему уравнений электростатики:
![]()
и не представляет никакой информации о динамике электрического поля. Этот вопрос нуждается в дополнительной проработке.
Перечень используемой литературыа) И. Е. Тамм. .Основы теории электричества., "Наука" 1976г.
б) Л. Д. Ландау, Е. М. Лифшиц. .Теория поля., "Наука" 1973г.
в) И. В. Савельев. .Курс общей физики., "Наука" 1978г.
2.
а) Б. М. Яворский, А. А. Детлафф. .Справочник по физике., "Наука" 1979г.
б) Г. Корн и Т. Корн. .Справочник по математике для инженеров и научных работников. (перевод с английского), "Наука" 1978г.
в) А. Н. Тихонов, А. А. Самарский. "Уравнения математической физики", "Наука" 1972г.
Похожие работы
... имеет обычный в таком случае вид [1], где . Тогда связи комплексных амплитуд запишутся для систем (3) и (4) как и , а для (1) и (2) и . Как видим, в данном случае распространение волн всех четырех составляющих реального электромагнитного поля подчиняется теоретически хорошо изученному закону для плоских волн ЭМ поля в металлах [1], когда волновые решения для проводящей среды имеют вид ...
... все волновые решения имеют вид экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами на . Однако вернемся к обсуждению энергетики распространения составляющих реального электромагнитного поля в виде плоских волн в диэлектрической среде без потерь (). Вначале обратимся к закону сохранения электрической энергии, соотношение которого согласно (10) запишется как: ...
... остановиться подробнее, потому что, мне кажется, сами того не осознавая, большинство наших современников, изучавших в школе физику, но не занимающиеся ею профессионально, придерживаются именно ньютоновского взгляда на пространство и время. В нашей критике Исаака Ньютона будем следовать Эрнсту Маху [6], давшему, на мой взгляд, самую основательную оценку трудов великого англичанина. Обратимся к ...
... в конечном счете и определяют направление и характер их деятельности, их цели и стремле- ния. Чтобы этот подход стал понятным, напомним следующее. Основной вопрос философии - это, по существу, проблема выявления оснований совпадения цели и результата практической деятельности. Поскольку практика - это деятельность и материальная (протекающая по законам природы, т.е. в формах объективного ...
0 комментариев