Навигация
Интерпретации в математическом моделировании
1.3. Интерпретации в математическом моделировании
Интерпретация (от латинского "interpretatio" - разъяснение, толкование, истолко-
вание) определяется как совокупность значений (смыслов), придаваемых каким-либо об-
разом элементам некоторой системы (теории), например, формулам и отдельным симво-
лам. В математическом аспекте интерпретация - это экстраполяция исходных положе-
ний какой-либо формальной системы на какую-либо содержательную систему, исход-
ные положения которой определяются независимо от формальной системы. Следова-
тельно, можно утверждать, что интерпретация - это установление соответствия между некоторой формальной и содержательной системами. В тех случаях, когда формальная система оказывается применимой (интерпретируемой) к содержательной системе, т.е. ус-
тановлено что между элементами формальной системы и элементами содержательной системы существует взаимно однозначное соответствие, все исходные положения фор-
мальной системы получают подтверждение в содержательной системе. Интерпретация считается полной, если каждому элементу формальной системы соответствует некото-
рый элемент (интерпретант) содержательной системы. Если указанное условие наруша-
ется, имеет место частичная интерпретация.
При математическом моделировании в результате интерпретации задаются значе-
ния элементов математических выражений (символов, операций, формул) и целостных конструкций.
Основываясь на приведенных общих положениях, определим содержание интер-
претации применительно к задаче математического моделирования.
Определение 3. Интерпретация в математическом моделировании - это информа-
ционный процесс преобразования абстрактного математического объекта (АМО) в кон-
кретную математическую модель (ММ) конкретного объекта на основе отображения
непустого информационного множества данных и знаний, определяемого АМО и называе-
мого областью интерпретации, в кообласть - информационное множество данных и зна-
ний, определяемое предметной областью и объектом моделирования и называемое об-
ластью значений интерпретации.
Таким образом, интерпретацию следует рассматривать как один из основопола-
гающих механизмов (инструментов) технологии математического (научного) модели-
рования.
Именно интерпретация, придавая смысл и значения элементам (компонентам) ма-
тематического выражения, делает последнее математической моделью реального объек-
та.
1.4. Виды и уровни интерпретаций
Создание математической модели системного элемента - многоэтапный процесс. Основным фактором, определяющим этапы перехода от АМО к ММ, является интер-
претация. Количество этапов и их содержание зависит от начального (исходного) ин-
формационного содержания интерпретируемого математического объекта - математи-
ческого описания и требуемого конечного информационного содержания математичес-
кого объекта - модели. Полный спектр этапов интерпретации, отражающий переход от АМО - описания к конкретной ММ, включает четыре вида интерпретаций: синтаксичес-
кую (структурную), семантическую(смысловую), качественную(численную) и количес-
твенную. В общем случае, каждый из перечисленных видов интерпретации может иметь многоуровневую реализацию. Рассмотрим более подробно перечисленные виды интер-
претаций.
Cинтаксическая интерпретация
Синтаксическую интерпретацию будем рассматривать как отображение морфоло-
гической (структурной) организации исходного АМО в морфологическую организацию структуру заданного (или требуемого) АМО. Синтаксическая интерпретация может осуществляться как в рамках одного математического языка, так и различных матема-
тических языков.
При синтаксической интерпретации АМО возможны несколько вариантов задач реализации.
Задача 1. Пусть исходный АМО не структурирован, например, задан кортежем элементов. Требуется посредством синтаксической интерпретации сформировать мор-
фологическую структуру математического выражения
![]() (1)
(1)
Задача 2. Пусть АМО имеет некоторую исходную морфологическую структуру,
которая по тем или иным причинам не удовлетворяет требованиям исследователя (эксперта). Требуется посредством синтаксической интерпретации преобразовать в со-
ответствии с целями и задачами моделирования исходную структуру St![]() в адекватную требуемую St
в адекватную требуемую St![]() ,т.е.
,т.е.
![]() (2)
(2)
Задача 3. Пусть АМО имеет некоторую исходную морфологическую структуру St![]() , удовлетворяющую общим принципам и требованиям исследователя с точки зрения её синтаксической организации. Требуется посредством синтаксической интерпретации конкретизировать АМО со структурой St
, удовлетворяющую общим принципам и требованиям исследователя с точки зрения её синтаксической организации. Требуется посредством синтаксической интерпретации конкретизировать АМО со структурой St![]() до уровня требований, определяемых целями и задачами моделирования
до уровня требований, определяемых целями и задачами моделирования
![]() (3)
(3)
Таким образом, синтаксическая интерпретация математических объектов даёт воз-
можность формировать морфологические структуры АМО, осуществлять отображение (транслировать) морфологические структуры АМО с одного математического языка на другой, конкретизировать или абстрагировать морфологические структурные представ-
ления АМО в рамках одного математического языка.
Семантическая интерпретация
Семантическая интерпретация предполагает задание смысла математических вы-
ражений, формул, конструкций, а также отдельных символов и знаков в терминах сфе-
ры, предметной области и объекта моделирования. Семантическая интерпретация даёт возможность сформировать по смысловым признакам однородные группы, виды, клас-
сы и типы объектов моделирования. В зависимости от уровней обобщения и абстраги-
рования или, наоборот, дифференциации или конкретизации, семантическая интерпре-
тация представляется как многоуровневый, многоэтапный процесс.
Таким образом, семантическая интерпретация, задавая смысл абстрактному ма-
тематическому объекту, "переводит" последний в категорию математической модели с объекта-оригинала, в терминах которого и осуществляется такая интерпретация.
Качественная интерпретация
Интерпретация на качественном уровне предполагает существование качествен-
ных параметров и характеристик объекта-оригинала, в терминах (значениях) которых и производится интерпретация. При качественной интерпретации могут использоваться графические и числовые представления, посредством которых, например, интерпретиру-
ется режим функционирования объекта моделирования.
Количественная интерпретация
Количественная интерпретация осуществляется за счет включения в рассмотрение количественных целочисленных и рациональных величин, определяющих значение па-
раметров, характеристик, показателей.
В результате количественной интерпретации появляется возможность из класса, группы или совокупности аналогичных математических объектов выделить один един-
ственный, являющийся конкретной математической моделью конкретного объекта-ори-
гинала.
Таким образом, в результате четырех видов интерпретаций - синтаксической, се-
мантической, качественной и количественной происходит поэтапная трансформация
АМО, например, концептуальной метамодели (КММ) функциональной системы ![]() , в конкретную математическую модель (ММ) конкретного объекта моделирования.
, в конкретную математическую модель (ММ) конкретного объекта моделирования.
Глава II Концептуальное метамоделирование функционирования системного
элемента
Похожие работы
... КММ) функциональной системы , в конкретную математическую модель (ММ) конкретного объекта моделирования. Глава Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является одним из фундаментальных в общей теории систем (ОТС) - системологии. Оно происходит от латинского "Elementarius" и имеет смысл: начальный, ...
... модель (ММ) конкретного объекта моделирования.Глава II Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является одним из фундаментальных в общей теории систем (ОТС) - системологии. Оно происходит от латинского "Elementarius" и имеет смысл: начальный, простой, простейший, ...
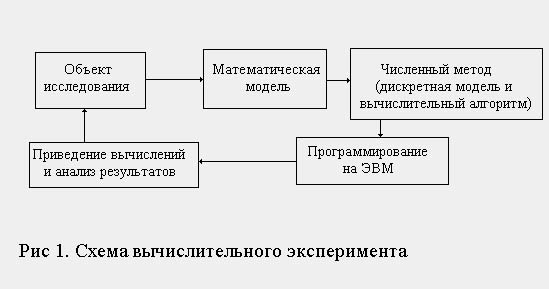
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
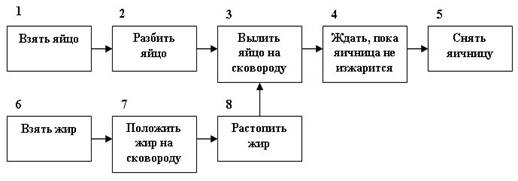
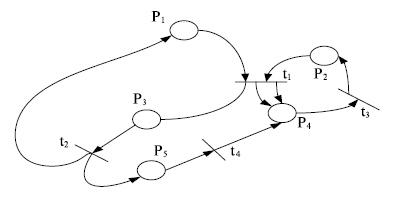
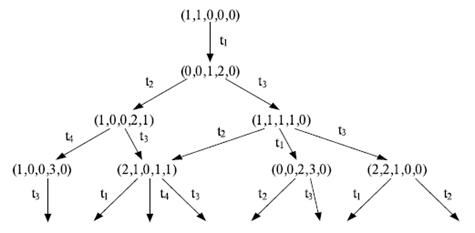
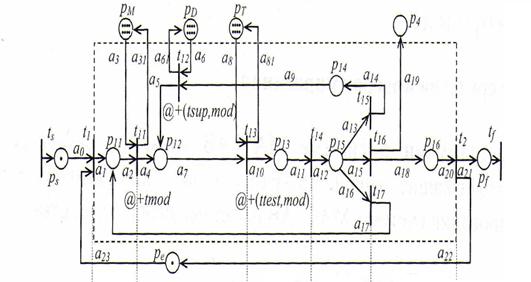
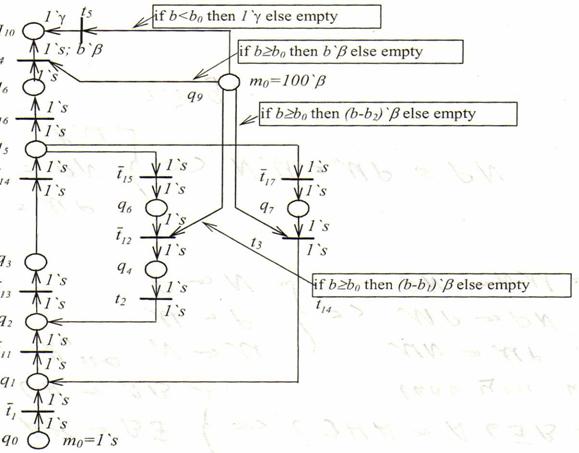
... cout << " предшествует элементу "; } // Поиск ведущих с нулевым количеством предшественников. A. Poisk (); // Фаза вывода. A. Vyvod (); } [11] §3. Математические модели с использованием сетей Петри Сети Петри являются эффективным инструментом дискретных процессов, в частности, функционирования станочных систем. Их особенность заключается в возможности отображения параллелизма ...

0 комментариев