Навигация
Метод концептуального метамоделирования
2.4. Метод концептуального метамоделирования
Концептуальное метамоделирование ( КММ ) основано на использовании индук-
тивно-дедуктивного подхода. Создание КММ осуществляется на основе индуктивного подхода ( от конкретного к абстрактному, от частного к общему ) посредством обобще-
ния, концептуализации и формализации.
Использование КММ предполагает переходы от общего к частному, от абстракт-
ного к конкретному на основе интерпретаций.
КММ функционирования системного элемента ![]() предполагает описание динами-
предполагает описание динами-
ки поведения на заданном уровне абстракции с точки зрения его взаимодействия с окру-
жающей средой, т.е. внешнего поведения. Математическое описание такого элемента должно отражать последовательность причинно-следственных связей типа "вход - вы-
ход" с заданной временной направленностью из прошлого в будущее. КММ функциони-
рования системного элемента ![]() должна учитывать базовые концепции и существенные факторы, к числу которых, в первую очередь, следует отнести следующие.
должна учитывать базовые концепции и существенные факторы, к числу которых, в первую очередь, следует отнести следующие.
1. Элемент ![]() , как компонент системы
, как компонент системы ![]() , связан и взаимодействует с другими компонентами этой системы.
, связан и взаимодействует с другими компонентами этой системы.
2. Компоненты ![]() системы
системы ![]() воздействуют на элемент
воздействуют на элемент ![]() посредст-
посредст-
вом входных сигналов, в общем случае, обозначаемых векторным множеством ![]() .
.
3. Элемент ![]() может выдавать в окружающую его среду
может выдавать в окружающую его среду ![]() выходные сигна-лы, обозначаемые векторным множеством
выходные сигна-лы, обозначаемые векторным множеством ![]() .
.
4. Функционирование системного элемента ![]() (
( ![]() ) происходит во време-
) происходит во време-
ни с заданной временной направленностью от прошлого к будущему: ![]() где
где ![]()
5. Процесс функционирования элемента ![]() представляется в форме отображения
представляется в форме отображения ![]() входного векторного множества
входного векторного множества ![]() в выходное -
в выходное - ![]() , т.е. по схеме "вход - выход" и представляется записью вида
, т.е. по схеме "вход - выход" и представляется записью вида
![]() .
.
6. Структура и свойства отображения ![]() при моделировании на основе метода прямых аналогий определяется внутренними свойствами элемента
при моделировании на основе метода прямых аналогий определяется внутренними свойствами элемента ![]() , во всех остальных случаях - инвариантны и связаны феноменологически.
, во всех остальных случаях - инвариантны и связаны феноменологически.
7. Совокупность существенных внутренних свойств элемента ![]() , представ-ляется в модели "срезом" их значений для фиксированного момента времени
, представ-ляется в модели "срезом" их значений для фиксированного момента времени ![]() , при
, при
условии фиксированного "среза" значений входных воздействий ![]() и опреде-
и опреде-
ляется как внутреннее состояние ![]() элемента
элемента ![]() .
.
8. Внутренние свойства элемента ![]() характеризуются вектором параметров
характеризуются вектором параметров
![]() , которые назовем функциональными ( j - параметры ).
, которые назовем функциональными ( j - параметры ).
Концептуальное математическое описание системного
элемента ![]() (
( ![]() )
)
с учетом изложенных выше положений, представим кортежем
![]() .
( 1 )
.
( 1 )
Такое описание определим как концептуальную метамодель - КММ функционирования системного элемента ![]() .
.
Похожие работы
... КММ) функциональной системы , в конкретную математическую модель (ММ) конкретного объекта моделирования. Глава Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является одним из фундаментальных в общей теории систем (ОТС) - системологии. Оно происходит от латинского "Elementarius" и имеет смысл: начальный, ...
... модель (ММ) конкретного объекта моделирования.Глава II Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является одним из фундаментальных в общей теории систем (ОТС) - системологии. Оно происходит от латинского "Elementarius" и имеет смысл: начальный, простой, простейший, ...
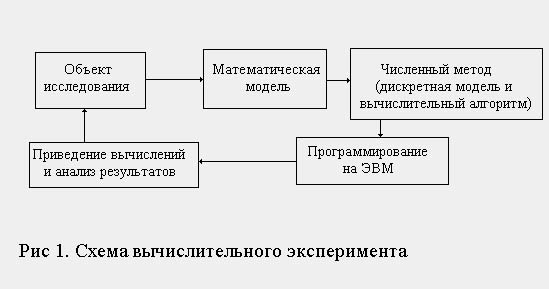
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
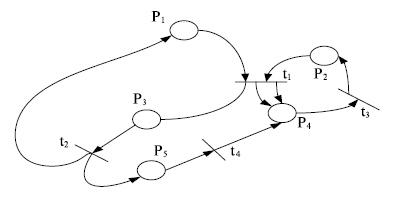
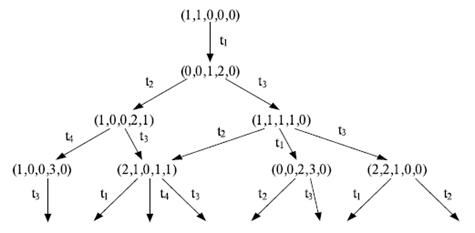
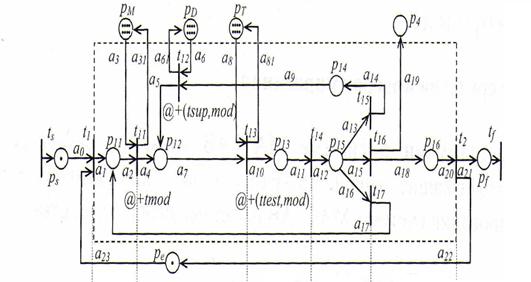
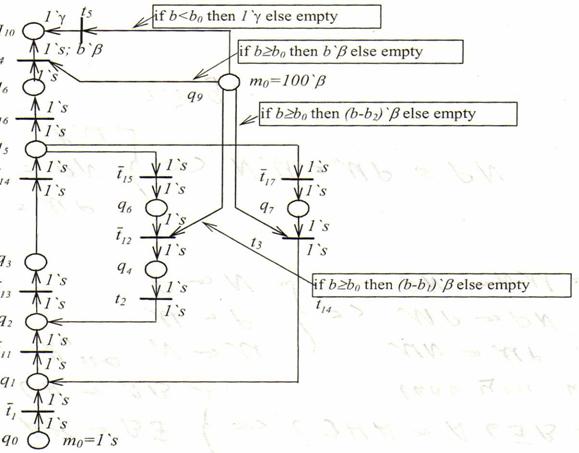
... cout << " предшествует элементу "; } // Поиск ведущих с нулевым количеством предшественников. A. Poisk (); // Фаза вывода. A. Vyvod (); } [11] §3. Математические модели с использованием сетей Петри Сети Петри являются эффективным инструментом дискретных процессов, в частности, функционирования станочных систем. Их особенность заключается в возможности отображения параллелизма ...

0 комментариев