Навигация
Целостность системного элемента
28499
знаков
0
таблиц
0
изображений
2.3. Целостность системного элемента
Целостность одно из основных свойств (атрибутов) системного элемента. Она от-
ражает завершенную полноту его дискретного строения. Правильно сформированный
системный элемент 
(
) характеризуется явно выраженной обособленностью (границами) и определенной степенью независимости от окружающей его среды. Относительная независимость системного элемента определяется (характеризуется) совокупностью факторов, которые назовем факторами целостности.
Факторы целостности Полная совокупность факторов целостности элемента определяется двумя группами, которые назовем внешние факторы целостности и внут-ренние.
Внешние факторы 1. Низкий уровень связности (число взаимосвязей) элемента 
с ок-ружающей его средой 
, т.е. минимальная внешняя связность элемента . Обозначив полную совокупность внешних связей элемента через 
, рассматриваемый фактор запишем как условие минимизации: ® Min.
2. Низкий уровень взаимодействия 
элемента с окружающей его средой
,т.е. слабое взаимодействие, определяемое минимальной совокупной интенсивностью обмена сигналами ® Min.
Внутренние факторы 1. Высокая степень связности друг с другом частей, из которых состоит элемент , т.е. суммарная внутренняя связность 
максимальна ®Max.
2. Высокая интенсивность 
взаимодействия частей, из которых состоит элемент . Иными словами, имеет место сильное внутреннее взаимодействие ®Max.
Оценка целостности элемента Перечисленные выше факторы могут быть использова-
ны для оценки целостности системного элемента . Такая оценка, в определенной мере, характеризует степень "прочности" элемента по отношению к окружающей его
среде .
Введем понятие "прочность" как показатель внутренней целостности элемента и
определим его через суммарную композицию показателей взаимосвязей и взаимо-
действий всех частей, из которых состоит элемент . Прочность элемента при
этом определяется выражением
(1)
Для обобщенной оценки внешних взаимосвязей и взаимодействий элемента
с окружающей его средой введем показатель "сцепленности" и определим его как композицию показателей и , т.е.
(2)
Полученные показатели прочности (1) и сцепленности (2) используем для оценки
целостности 
элемента . Такая оценка определяется отношением вида
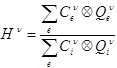(3)
т.е. как отношение прочности 
элемента к его сцепленности 
со средой .
С учетом (1) и (2) выражение (3) принимает вид
(4)
Уровни целостности элемента Анализ выражений (3) и (4) дает возможность ранжи-ровать элементы по уровням целостности и качественно определить их устойчи-вость по отношению к окружающей среде.
Случай 1. Если значение показателя прочности элемента превосходит зна-
чение показателя сцепленности элемента с его средой , т.е. > , а как
следствие и > 1, то элемент по своим целостным свойствам устойчив. В рассмат-
риваемом случае имеет место супераддитивная целостность.
Случай 2. Пусть значения показателей прочности и сцепленности равны,
т.е. = . В этом случае показатель целостности = 1. Тогда элемент по сво-
им целостным свойствам находится на грани устойчивости. Такой уровень целостности элемента определим как аддитивная целостность.
Случай 3. Наконец, пусть значения показателя прочности элемента ниже значений показателя сцепленности элемента с его средой . В рассматривае-
мом случае условия записываются в виде < и < 1. При этом элемент по сво-
им целостным свойствам не устойчив к интегральному вовлечению (растворению) в окружающей среде . Рассматриваемый уровень целостности элемента определим
как субаддитивная целостность.
Таким образом, введенный показатель может использоваться как критерий
оценки качества целостных свойств элемента , а также для сравнения раэличных элементов (n = 1, 2, ... , N) по критерию целостности.
Похожие работы
... КММ) функциональной системы , в конкретную математическую модель (ММ) конкретного объекта моделирования. Глава Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является одним из фундаментальных в общей теории систем (ОТС) - системологии. Оно происходит от латинского "Elementarius" и имеет смысл: начальный, ...
... модель (ММ) конкретного объекта моделирования.Глава II Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является одним из фундаментальных в общей теории систем (ОТС) - системологии. Оно происходит от латинского "Elementarius" и имеет смысл: начальный, простой, простейший, ...
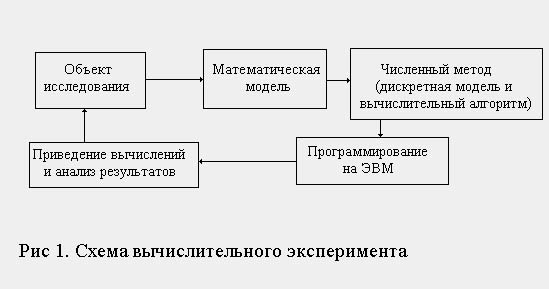
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
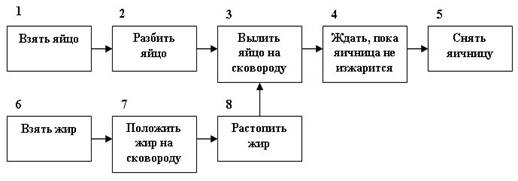
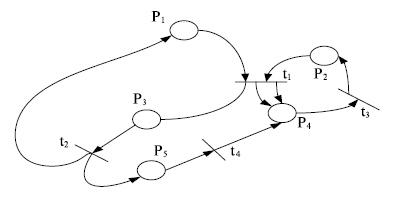
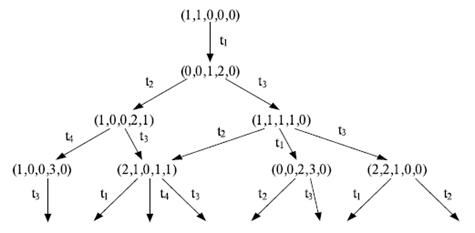
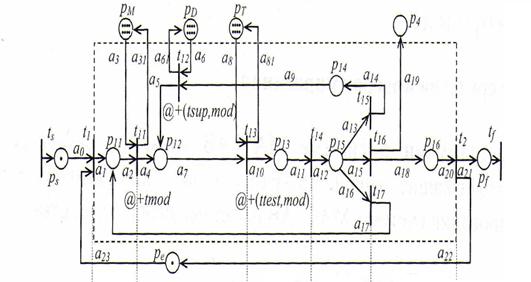
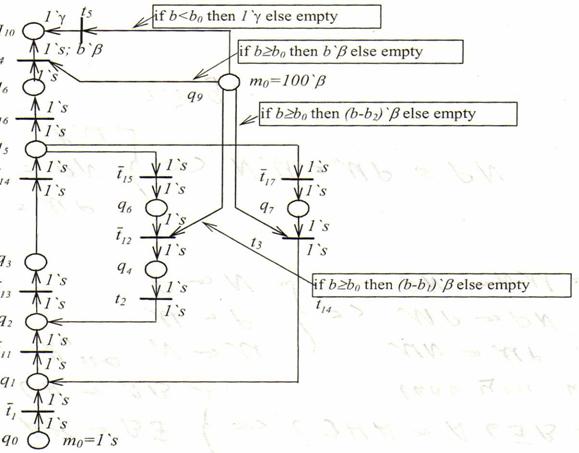
... cout << " предшествует элементу "; } // Поиск ведущих с нулевым количеством предшественников. A. Poisk (); // Фаза вывода. A. Vyvod (); } [11] §3. Математические модели с использованием сетей Петри Сети Петри являются эффективным инструментом дискретных процессов, в частности, функционирования станочных систем. Их особенность заключается в возможности отображения параллелизма ...
0 комментариев