Навигация
Стратифицированный анализ и описание КММ системного элемента
2.5. Стратифицированный анализ и описание КММ системного элемента
Концептуальные метамодели элемента, основанные на записи ( 1 ), могут образо-
вывать некоторые иерархии. Уровни таких иерархий определяются степенью ( этапами ) конкретизации свойств элемента. Ранжирование КММ ( 1 ) по шкале "Абстрактное - Конкретное" на основе метода стратификации, следовательно, приводит к иерархичес-
кой дедуктивной системе концептуальных метамоделей. Такая система может быть ис-
пользована для математического моделирования конкретных элементов как некоторый исходный базовый инвариант, интерпретируемый в конкретную математическую мо-
дель.
В зависимости от степени конкретизации, сформируем дедуктивную систему, вклю-чающую следующие уровни КММ элемента ![]() :
:
КММ элемента ![]() на теоретико-системном уровне ( ТСУ );
на теоретико-системном уровне ( ТСУ );
КММ элемента ![]() на уровне непараметрической статики ( УНС );
на уровне непараметрической статики ( УНС );
КММ элемента ![]() на уровне параметрической статики ( УПС );
на уровне параметрической статики ( УПС );
КММ элемента ![]() на уровне непараметрической динамики ( УНД );
на уровне непараметрической динамики ( УНД );
КММ элемента ![]() на уровне параметрической динамики ( УПД ).
на уровне параметрической динамики ( УПД ).
Рассмотрим более подробно КММ на каждом из перечисленных уровней.
КММ теоретико-системного уровня
Наиболее общую и абстрактную форму описания функционирования системного
элемента ![]() дает концептуальная метамодель теоретико-системного уровня ( ТСУ ). Это описание включает векторное множество входных воздействий на элемент
дает концептуальная метамодель теоретико-системного уровня ( ТСУ ). Это описание включает векторное множество входных воздействий на элемент ![]()
![]()
и векторное множество выходных реакций ( откликов ) элемента ![]()
![]() .
.
Кроме того, на рассматриваемом уровне абстракции учитывается факт связности век-
торного множества ![]() с соответствующим векторным множеством
с соответствующим векторным множеством ![]() посредством отображения "j". Однако, отображение "j" не указывает каким образом рассматривае-
посредством отображения "j". Однако, отображение "j" не указывает каким образом рассматривае-
мые множества связаны.
Таким образом, КММ теоретико-системного уровня задаются тройкой
![]() . ( 2 )
. ( 2 )
КММ уровня непараметрической статики
Второй уровень представления КММ включает в рассмотрение отображение ![]() , определяющее правила преобразования входов
, определяющее правила преобразования входов ![]() в выходы
в выходы ![]() , т.е. что необходимо сделать, чтобы при условии
, т.е. что необходимо сделать, чтобы при условии ![]() получить
получить ![]() , адекватное целевому функционированию элемента
, адекватное целевому функционированию элемента ![]() . В общем случае
. В общем случае ![]() - отображение может быть представлено скалярной или векторной функцией, а также функционалом или оператором. Концептуальная метамо-
- отображение может быть представлено скалярной или векторной функцией, а также функционалом или оператором. Концептуальная метамо-
дель уровня непараметрической статики, следовательно, представляется кортежем вида
![]() .
( 3 )
.
( 3 )
Раскрытие структуры преобразования вида ![]() является основной задачей КММ уровня
является основной задачей КММ уровня ![]() . Рассмотрим в качестве иллюстрации функциональное описание элемента
. Рассмотрим в качестве иллюстрации функциональное описание элемента ![]() , представленное скалярной функцией
, представленное скалярной функцией ![]() , причем:
, причем: ![]() .
.
Функционирование элемента ![]() (
( ![]() ) на УНС описывается как отобра-
) на УНС описывается как отобра-
жение ![]() . Это отображение называется функцией, если оно однозначно. Ус-
. Это отображение называется функцией, если оно однозначно. Ус-
ловия однозначности определяются следующим образом. Пусть заданы пары значений
сигналов "вход - выход":
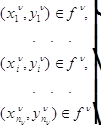 ( 4 )
( 4 )
Если из условия ( ![]() ), следует, что (
), следует, что ( ![]() ), то отображе-
), то отображе-
ние ![]() однозначно. Значение величины
однозначно. Значение величины ![]() в любой из пар
в любой из пар ![]() называется функ-
называется функ-
цией от данного ![]() . Общий вид записи функции
. Общий вид записи функции ![]() позволяет дать формальное
позволяет дать формальное
определение функции элемента ![]() в скалярной форме представления
в скалярной форме представления
![]() ( 5 )
( 5 )
Таким образом, КММ ( 3 ) проинтерпретирована в КММ того же уровня, но в скаляр-
ной форме функционального представления. Отметим, что богатство концептуальных метамоделей ![]() функционирования системного элемента
функционирования системного элемента ![]() (
( ![]() ) на уровне непараметрической статики определяется многообразием ее интерпретаций на матема-
) на уровне непараметрической статики определяется многообразием ее интерпретаций на матема-
тическом, логическом или логико-математическом языках описания ( представления )
![]() - отображения.
- отображения.
КММ уровни параметрической статики
Дальнейшая конкретизация КММ функционирования системного элемента ![]()
осуществляется за счет включения в рассмотрение функциональных параметров ![]() , определяющих статические режимы. Для элемента
, определяющих статические режимы. Для элемента ![]() рассматриваются три группы параметров
рассматриваются три группы параметров
![]() ( 6 )
( 6 )
где ![]() - совокупность параметров {
- совокупность параметров { ![]() } входных воздействий
} входных воздействий ![]()
![]() - совокупность параметров {
- совокупность параметров { ![]() } выходных реакций ( откликов )
} выходных реакций ( откликов ) ![]()
![]() - совокупность параметров {
- совокупность параметров { ![]() } отображения
} отображения ![]() .
.
Перечни ( номенклатура ) параметров ![]() и их значений определяются для каждого ти-
и их значений определяются для каждого ти-
па конкретной модели ![]() . Для
. Для ![]() - отображения, по аналогии со структурными моде- лями, вводится понятие конфигурации. С учетом параметрического описания и интер-
- отображения, по аналогии со структурными моде- лями, вводится понятие конфигурации. С учетом параметрического описания и интер-
претаций КММ задается четверкой
![]() ( 7 )
( 7 )
КММ уровня непараметрической динамики
Следующий, четвертый уровень конкретизации КММ функционирования систем-
ного элемента ![]() определяется учетом в модели его динамических свойств. Динамика элемента
определяется учетом в модели его динамических свойств. Динамика элемента ![]() рассматривается в нескольких аспектах. Первый аспект характеризуется реакцией элемента
рассматривается в нескольких аспектах. Первый аспект характеризуется реакцией элемента ![]() на динамику изменения входных воздействий
на динамику изменения входных воздействий ![]()
при неизменном отображении ![]() , т.е. когда
, т.е. когда ![]() - скалярная или векторная функция. Второй аспект определяется реакцией элемента
- скалярная или векторная функция. Второй аспект определяется реакцией элемента ![]() на входные ( статические
на входные ( статические ![]() или ди-
или ди-
намические ![]() ) воздействия при времязависимом отображении
) воздействия при времязависимом отображении ![]() , т.е. когда
, т.е. когда ![]() -
-
функционал или оператор, зависящий от времени ![]() .
.
При изложенных условиях КММ рассматриваемого уровня абстракции представ-
ляется кортежем, включающем следующие четыре компоненты
![]() ( 8 )
( 8 )
Отметим, что на данном уровне представления КММ время ![]() указывает на факт
указывает на факт
наличия динамических свойств, но не характеризует их конкретно.
КММ уровня параметрической динамики
Последний - пятый уровень дедуктивного представления КММ функционирова-
ния системного элемента ![]() , определяемый как уровень параметрической динамики, включает все рассмотренные ранее аспекты модели, представляемые кортежем ( 1 )
, определяемый как уровень параметрической динамики, включает все рассмотренные ранее аспекты модели, представляемые кортежем ( 1 )
![]() .
.
В КММ рассматриваемого уровня выполняются условия концептуальной полноты представления функциональных свойств элемента ![]() . Интерпретация та- кой модели на семантическом, синтаксическом, качественном и количественном уров-
. Интерпретация та- кой модели на семантическом, синтаксическом, качественном и количественном уров-
нях дает возможность порождать ( генерировать ) любые конкретные математические модели функционирования системного элемента.
Отметим, что выражения ( 1 ), ( 2 ), ( 3 ), ( 7 ) и ( 8 ) могут быть представлены в форме традиционных аналитических зависимостей вида
![]() ( 9 )
( 9 )
Выводы
Таким образом, концептуальное метамоделирование функционирования систем-
ного элемента ![]() на основе дедуктивного подхода приводит к пятиуровневой иерархии моделей, представленной на рис. .
на основе дедуктивного подхода приводит к пятиуровневой иерархии моделей, представленной на рис. .
Практическое использование представленных выше КММ для моделирования функций системных элементов ![]() осуществляется посредством их ретрансляции в тер-минах выбранного математического языка и последующей интерпретации на четырех перечисленных выше уровнях конкретизации.
осуществляется посредством их ретрансляции в тер-минах выбранного математического языка и последующей интерпретации на четырех перечисленных выше уровнях конкретизации.
Похожие работы
... КММ) функциональной системы , в конкретную математическую модель (ММ) конкретного объекта моделирования. Глава Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является одним из фундаментальных в общей теории систем (ОТС) - системологии. Оно происходит от латинского "Elementarius" и имеет смысл: начальный, ...
... модель (ММ) конкретного объекта моделирования.Глава II Концептуальное метамоделирование функционирования системного элемента 2.1. Системный элемент как объект моделирования Понятие "элемент" является одним из фундаментальных в общей теории систем (ОТС) - системологии. Оно происходит от латинского "Elementarius" и имеет смысл: начальный, простой, простейший, ...
... целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]). ...
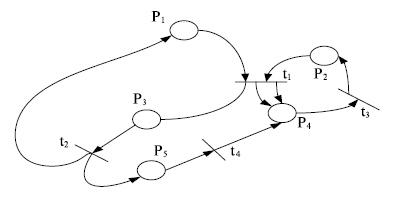
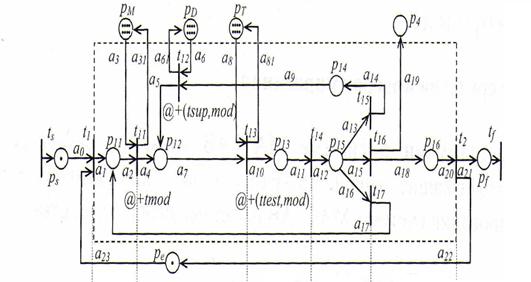
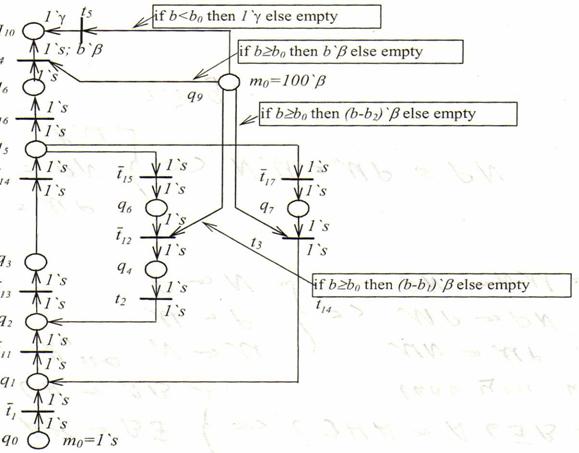
... cout << " предшествует элементу "; } // Поиск ведущих с нулевым количеством предшественников. A. Poisk (); // Фаза вывода. A. Vyvod (); } [11] §3. Математические модели с использованием сетей Петри Сети Петри являются эффективным инструментом дискретных процессов, в частности, функционирования станочных систем. Их особенность заключается в возможности отображения параллелизма ...

0 комментариев