£ Dy/Dx < ½ (ошибка <0)
Окружность в первом квадранте. 2.5 Выбор пикселов в первом квадранте
Системы координаты строк сканирования
Необходимость удаления невидимых линий
Обработка нижней стороны поверхности
Эффект зазубренного ребра
Xребра = x
Не лицевые плоскости
Схема решения относительно a и t
Простая трассировка лучей
Пересечение прямоугольной области в преобразованной системе координат
Навигация
Обработка нижней стороны поверхности
Трёхмерная компьютерная графика
103587
знаков
0
таблиц
24
изображения
3.4 Обработка нижней стороны поверхности
Для хранения максимальных значений y при каждом значении x используется массив, длина которого равна числу различимых точек (разрешению) по оси x в пространстве изображения. Значения, хранящиеся в этом массиве, представляют собой текущие значения “горизонта”. Поэтому по мере рисования каждой очередной кривой этот горизонт “всплывает”. Фактически этот алгоритм удаления невидимых линий работает каждый раз с одной линией.
Алгоритм работает очень хорошо до тех пор, пока какая-нибудь очередная кривая не окажется ниже самой первой из кривых. Как показано на рис.3.4,а. Подобные кривые, естественно, видимы и представляют собой нижнюю сторону исходной поверхности. Однако алгоритм будет считать их невидимыми. Нижняя сторона поверхности делается видимой, если модифицировать этот алгоритм, включив в него нижний горизонт, который опускается вниз по ходу работы алгоритма. Это реализуется при помощи второго массива, длина которого равна числу различимых точек по оси x в пространстве изображения. Этот массив содержит наименьшие значения y для каждого значения x. Алгоритм теперь становится таким:
Если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом x, то текущая кривая видима. В противном случае она невидима.
Полученный результат показан на рис. 3.4, b.
В изложенном алгоритме предполагается, что значение функции, т. е. y, известно для каждого значения x в пространстве изображения. Однако если для каждого значения x нельзя указать (вычислить) соответствующее ему значение у, то невозможно поддерживать массивы верхнего и нижнего плавающих горизонтов. В таком случае используется линейная интерполяция значений у между известными значениями для того, чтобы заполнить массивы верхнего и нижнего плавающих горизонтов, как показано на рис. 3.5.
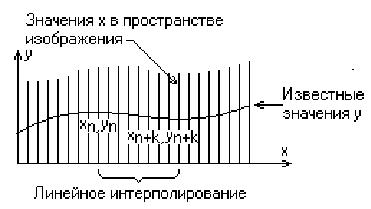
3.5 Линейная интерполяция между заданными точками
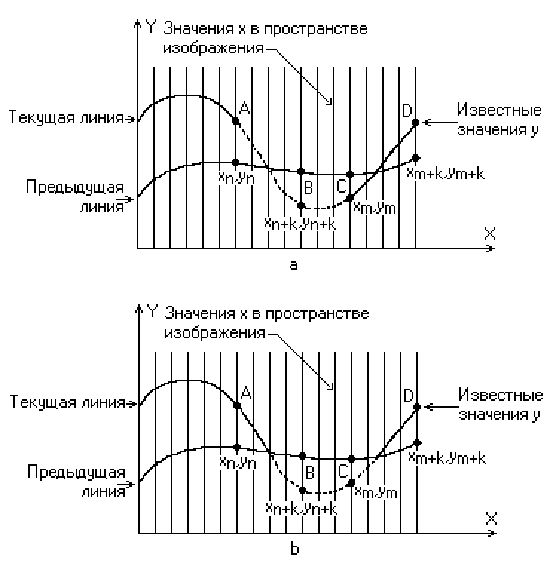
3.6. Эффект пересекающихся кривых
Если видимость кривой меняется, то метод с такой простой интерполяцией не даст корректного результата. Этот эффект проиллюстрирован рис. 3.6,а. Предполагая, что операция по заполнению массивов проводится после проверки видимости, получаем, что при переходе текущей кривой от видимого к невидимому состоянию (сегмент АВ на рис. 3.6,а), точка (xn+k, yn+k ) объявляется невидимой. Тогда участок кривой между точками (xn, yn) и (xn+k, yn+k ) не изображается и операция по заполнению массивов не производится. Образуется зазор между текущей и предыдущей кривыми Если на участке текущей кривой происходит переход от невидимого состояния к видимому (сегмент CD на рис. 3.6,а), то точка (xm+k, ym+k ) объявляется видимой, а участок кривой между точками (xm, ym) и (xm+k, ym+k ) изображается и операция по заполнению массивов проводится. Поэтому изображается и невидимый кусок сегмента CD. Кроме того, массивы плавающих горизонтов не будут содержать точных значений у. А это может повлечь за собой дополнительные нежелательные эффекты для последующих кривы. Следовательно,
необходимо решать задачу о поиске точек пересечения сегментов текущей и предшествующей кривых.
Существует несколько методов получения точек пересечения кривых. На растровых дисплеях значение координаты x можно увеличивать на 1, начиная с xn или xm (рис. 3.6,а). Значение у, соответствующее текущему значению координаты х в пространстве изображения, получается путем добавления к значению у, соответствующему предыдущему значению координаты x, вертикального приращения Dy вдоль заданной кривой. Затем определяется видимость новой точки с координатами (x + 1, y + Dy). Если эта точка видима, то активируется связанный с ней пиксел. Если невидима, то пиксел не активируется, а x увеличивается на 1. Этот процесс продолжается до тех пор, пока не встретится xn+k или xm+k. Пересечения для растровых дисплеев определяются изложенным методом с достаточной точностью. Близкий и даже более элегантный метод определения пересечений основан на двоичном поиске.
Точное значение точки пересечения двух прямолинейных отрезков, которые интерполируют текущую и предшествующую кривые, между точками (xn, yn) и (xn+k, yn+k ) (рис. 3.6) задается формулами:
где
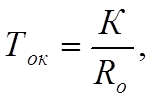
а индексы c и p соответствуют текущей и предшествующей кривым. Полученный результат показан на рис. 3.6,b. Теперь алгоритм излагается более формально.
Если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом x, то текущая кривая видима. В противном случае она невидима.
Если на участке от предыдущего (xn) до текущего (xn+k) значения x видимость кривой изменяется, то вычисляется точка пересечения (xi).
Если на участке от xn до xn+k сегмент кривой полностью видим, то он изображается целиком; если он стал невидимым, то изображается фрагмент от xn до xi; если же он стал видимым, то изображается фрагмент от xi до xn+k.
Заполнить массивы верхнего и нижнего плавающих горизонтов.
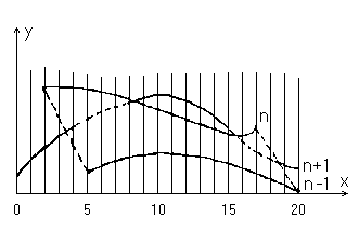
Изложенный алгоритм приводит к некоторым дефектам, когда кривая, лежащая в одной из более удаленных от точки наблюдения плоскостей, появляется слева или справа из-под множества кривых, лежащих в плоскостях, которые ближе к указанной точке наблюдения. Этот эффект продемонстрирован на рис. 3.7, где уже обработанные плоскости n - 1 и n расположены ближе к точке наблюдения. На рисунке показано, что получается при обработке плоскости n + 1. После обработки кривых n - 1 и n верхний горизонт для значений x = 0 и 1 равен начальному значению у; для значений x от 2 до 17 он равен ординатам кривой n; а для значений 18, 19, 20 - ординатам кривой n - 1. Нижний горизонт для значений x = 0 и 1 равен начальному значению у; для значений x = 2, 3, 4 – ординатам кривой n; а для значений x от 5 до 20 - ординатам кривой n - 1. При обработке текущей кривой (n + 1) алгоритм объявляет ее видимой при x = 4. Это показано сплошной линией на рис. 3.7.
Похожие работы
... Разновидности компьютерной графики Двумерная графика Двумерная компьютерная графика классифицируется по типу представления графической информации, и следующими из него алгоритмами обработки изображений. Обычно, компьютерную графику разделяют на: · векторную · растровую, · фрактальную Они отличаются принципами формирования изображения при отображении на экране монитора или при печати на ...
... в качестве реальной альтернативы системе Unix. _ 23.Платформа Intel ПК с процессором Intel продолжает оставаться наиболее распространённой платформой в сфере компьютерной графики и анимации. Главным событием, имеющим к ней непосредственное отноше- ние, стала демонстрация компанией Autodesk четвёртой версии программы 3D Studio - ...
... простыми. Большинство цветовых оттенков образуется смешением основных цветов. Способ разделения цветового оттенка на составляющие компоненты называется цветовой моделью. Существует много различных типов цветовых моделей, но в компьютерной графике, как правило, применяется не более трех. Эти модели известны под названиями: RGB, CMYK, НSB. Цветовая модель RGB Наиболее проста для понимания и ...
... прочие). В соответствии с принципами формирования изображения аддитивным или субтрактивным методами разработаны способы разделения цветового оттенка на составляющие компоненты, называемые цветовыми моделями. В компьютерной графике в основном применяют модели RGB и HSB (для создания и обработки аддитивных изображений) и CMYK (для печати копии изображения на полиграфическом оборудовании). Цветовые ...
0 комментариев