Навигация
Проверяем гипотезу о нормальности распределения оставшихся результатов измерений
22448
знаков
12
таблиц
161
изображение
3. Проверяем гипотезу о нормальности распределения оставшихся результатов измерений.
– Применяем критерий 1, вычисляем отношение
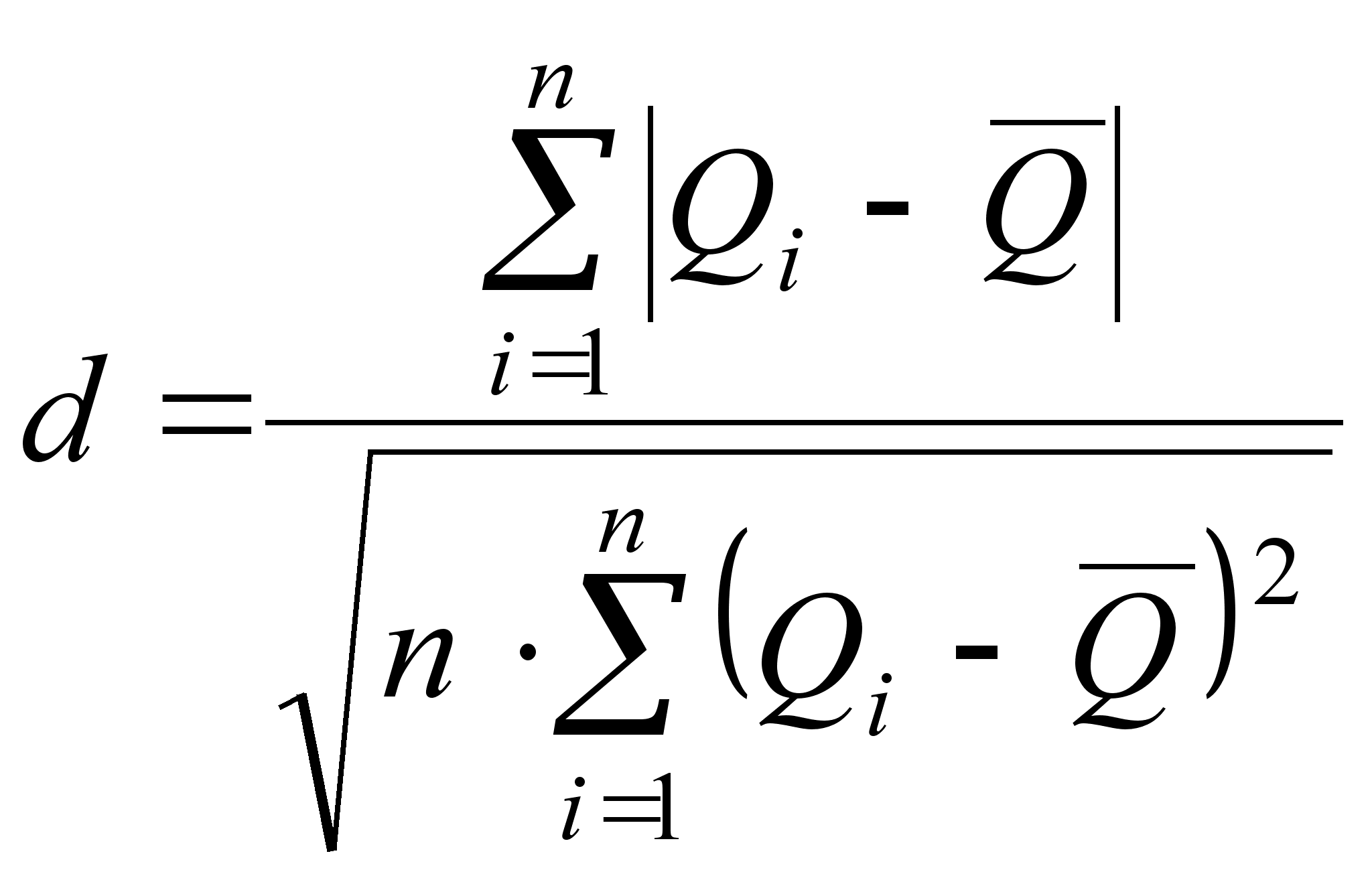(10)
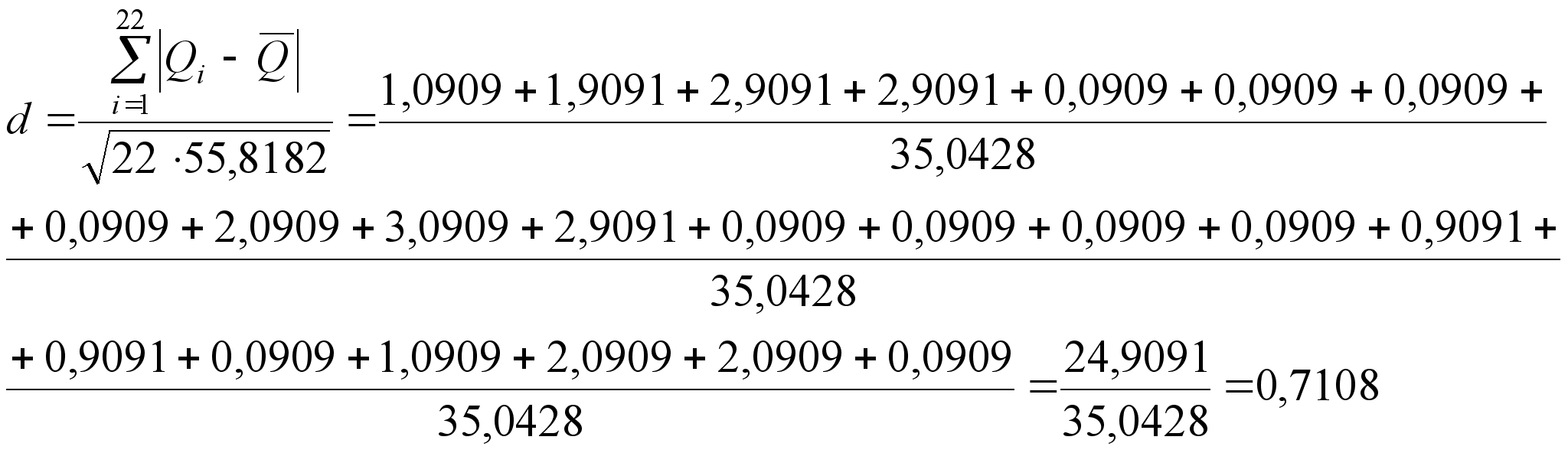
– задаемся
доверительной
вероятностью
P1
= 0,99 и для уровня
значимости
q1
= 1 – P1
по таблице П7
определяем
квантили
распределения
и 
,
,
для
n
= 22.
– сравниваем
с
и :
,
значит гипотеза
о нормальном
законе распределения
вероятности
результата
измерения
согласуется
с экспериментальными
данными, т.е.
результаты
наблюдений
можно считать
распределенными
нормально.
Так как n > 15, применяем критерий 2.
– задаемся доверительной вероятностью P2 = 0,98 и для уровня значимости q2 = 1 – P2 с учетом n = 22 определяем по таблице П8 значения m и P*. m = 2; P* = 0,97.
– для вероятности P* из таблиц для интегральной функции нормированного нормального распределения Ф(t) определяем значение t:
; (11)
при Ф(t) = 0,485 t = 2,17;
Рассчитываем E:
; (12)
;
Согласно
критерию 2 результаты
наблюдений
принадлежат
нормальному
закону распределения,
если не более
m
разностей 
превысили E.
Из таблицы 4
видно, что ни
одна разность
не превышает
E
= 3,4566. Следовательно,
гипотеза о
нормальном
законе распределения
вероятности
результата
измерения
согласуется
с экспериментальными
данными.
Соблюдаются
оба критерия,
значит закон
можно признать
нормальным
с вероятностью
,
.
4. Определяем стандартное отклонение среднего арифметического.
Так как закон распределения вероятности результата измерений признан нормальным, то стандартное отклонение определяем как:
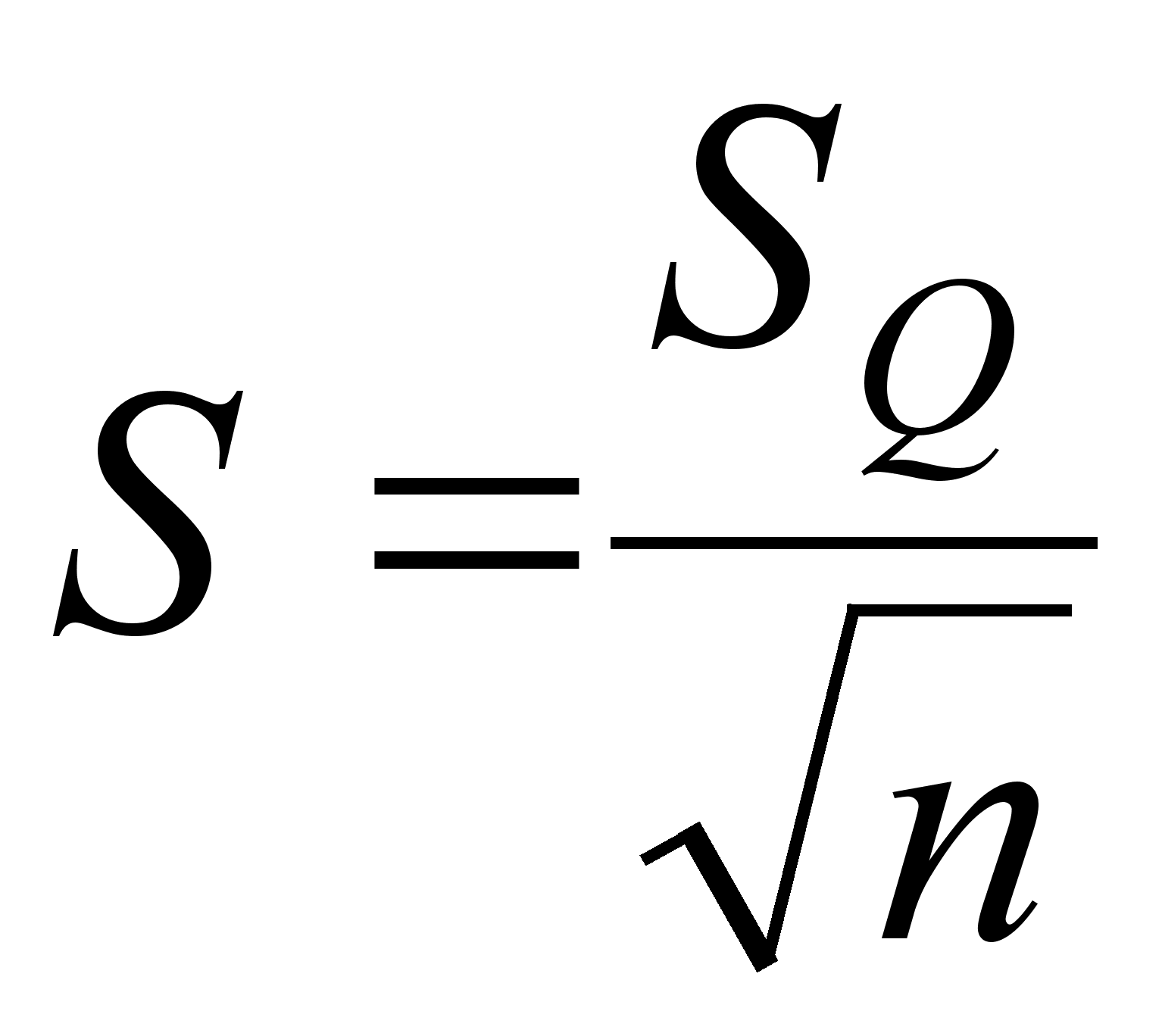(13)
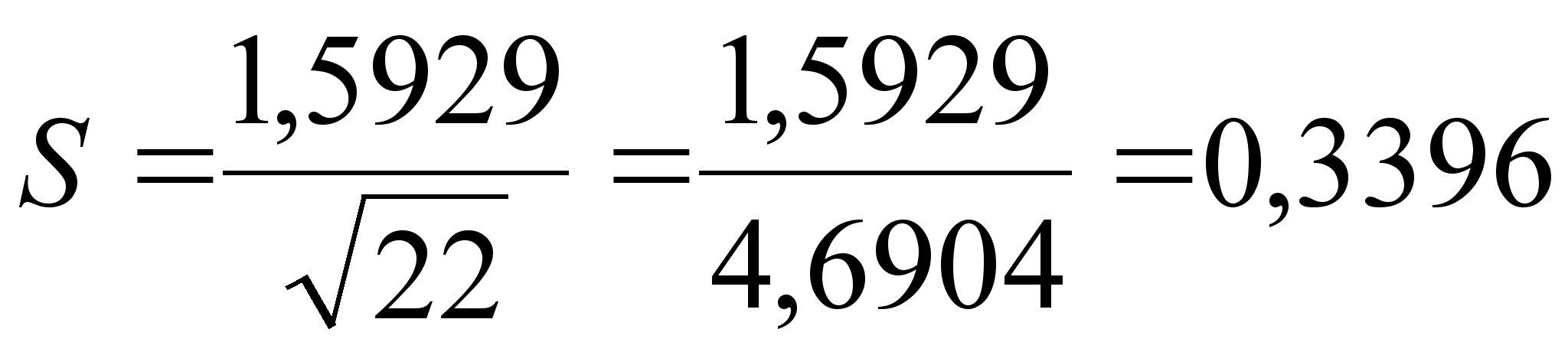
5. Определяем доверительный интервал.
Закон распределения вероятности результата измерений признан нормальным, поэтому доверительный интервал для заданной доверительной вероятности P определяется из распределения Стьюдента.
P
= 0,98;
; t
= 2,33;
; (14)
Значение Q будет находиться в пределах:
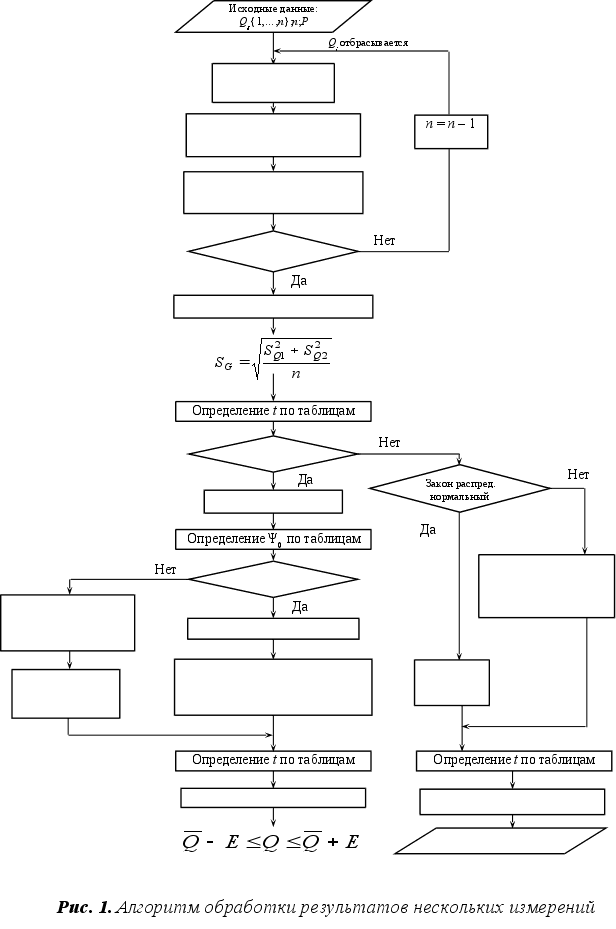
3. Обработка результатов нескольких серий измерений
Условие. При многократных измерениях одной и той же величины получены две серии по 12 (nj) результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице 5. Вычислить результат многократных измерений.
Исходные данные:
Таблица 5
| Серия 1 | Серия 2 | ||||||
| № изме-рения | Результат измерения | № изме-рения | Результат измерения | № изме-рения | Результат измерения | № изме-рения | Результат измерения |
| 1 | 482 | 7 | 483 | 1 | 483 | 7 | 483 |
| 2 | 485 | 8 | 483 | 2 | 483 | 8 | 482 |
| 3 | 486 | 9 | 481 | 3 | 483 | 9 | 481 |
| 4 | 486 | 10 | 480 | 4 | 483 | 10 | 481 |
| 5 | 483 | 11 | 492 | 5 | 484 | 11 | 483 |
| 6 | 483 | 12 | 486 | 6 | 484 | 12 | 495 |
Расчет.
1. Обрабатываем экспериментальные данные по алгоритму, изложенному в п.п. 1–3 задания 2, при этом:
– определяем
оценки результата
измерения 
и среднеквадратического
отклонения
;
– обнаруживаем и исключаем ошибки;
– проверяем гипотезу о нормальности распределения оставшихся результатов измерений.
(15)
(16)
Таблица 6
| Серия 1 | Серия 2 | ||||||
| № из-мерения | Результат измере-ния (Q1i) |
|
| № из-мерения | Результат измере-ния (Q2i) |
|
|
| 1 | 482 | -2,1667 | 4,6944 | 1 | 483 | -0,7500 | 0,5625 |
| 2 | 485 | 0,8333 | 0,6944 | 2 | 483 | -0,7500 | 0,5625 |
| 3 | 486 | 1,8333 | 3,3611 | 3 | 483 | -0,7500 | 0,5625 |
| 4 | 486 | 1,8333 | 3,3611 | 4 | 483 | -0,7500 | 0,5625 |
| 5 | 483 | -1,1667 | 1,3611 | 5 | 484 | 0,2500 | 0,0625 |
| 6 | 483 | -1,1667 | 1,3611 | 6 | 484 | 0,2500 | 0,0625 |
| 7 | 483 | -1,1667 | 1,3611 | 7 | 483 | -0,7500 | 0,5625 |
| 8 | 483 | -1,1667 | 1,3611 | 8 | 482 | -1,7500 | 3,0625 |
| 9 | 481 | -3,1667 | 10,0278 | 9 | 481 | -2,7500 | 7,5625 |
| 10 | 480 | -4,1667 | 17,3611 | 10 | 481 | -2,7500 | 7,5625 |
| 11 | 492 | 7,8333 | 61,3611 | 11 | 483 | -0,7500 | 0,5625 |
| 12 | 486 | 1,8333 | 3,3611 | 12 | 495 | 11,2500 | 126,5625 |
| Σ | 0 | 109,6667 | Σ | 0 | 148,2500 | ||
;
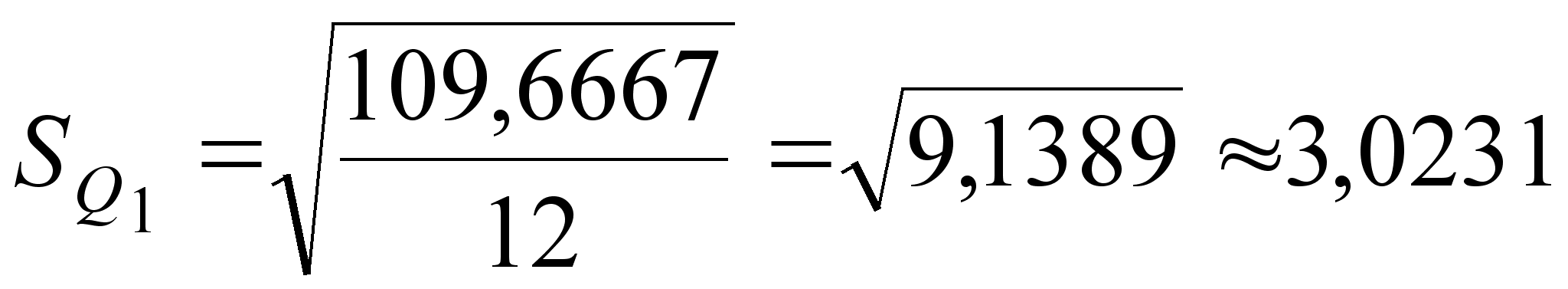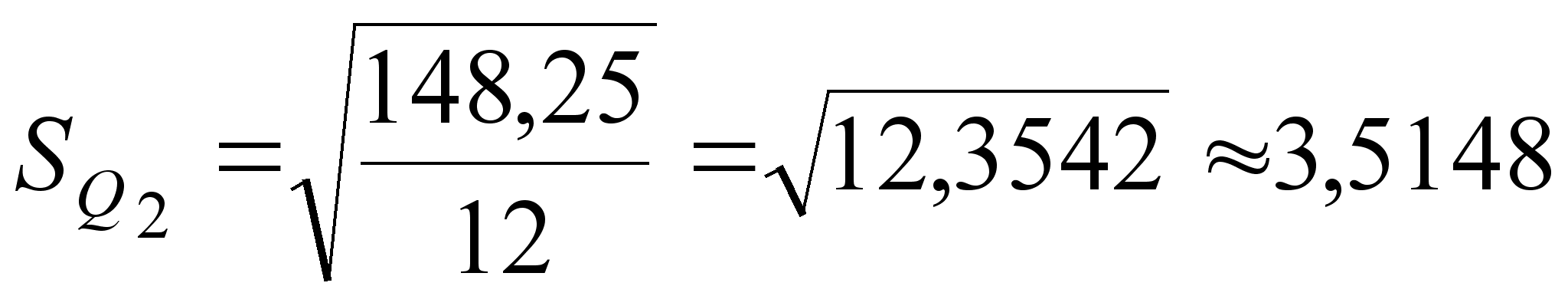
(17)
; 
;
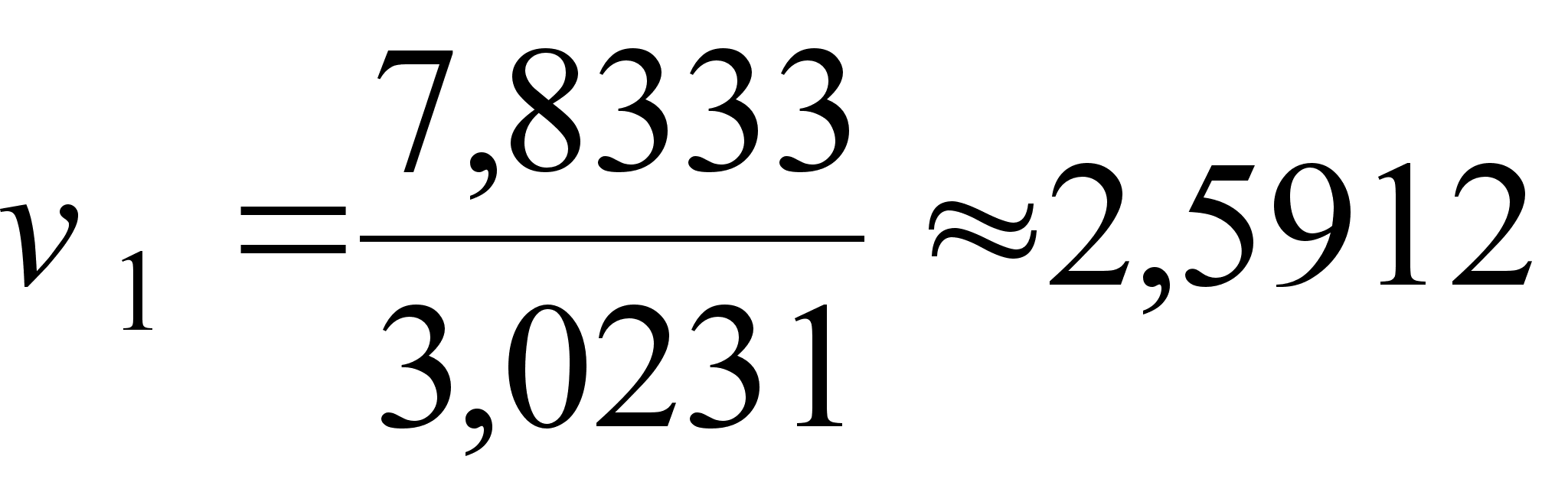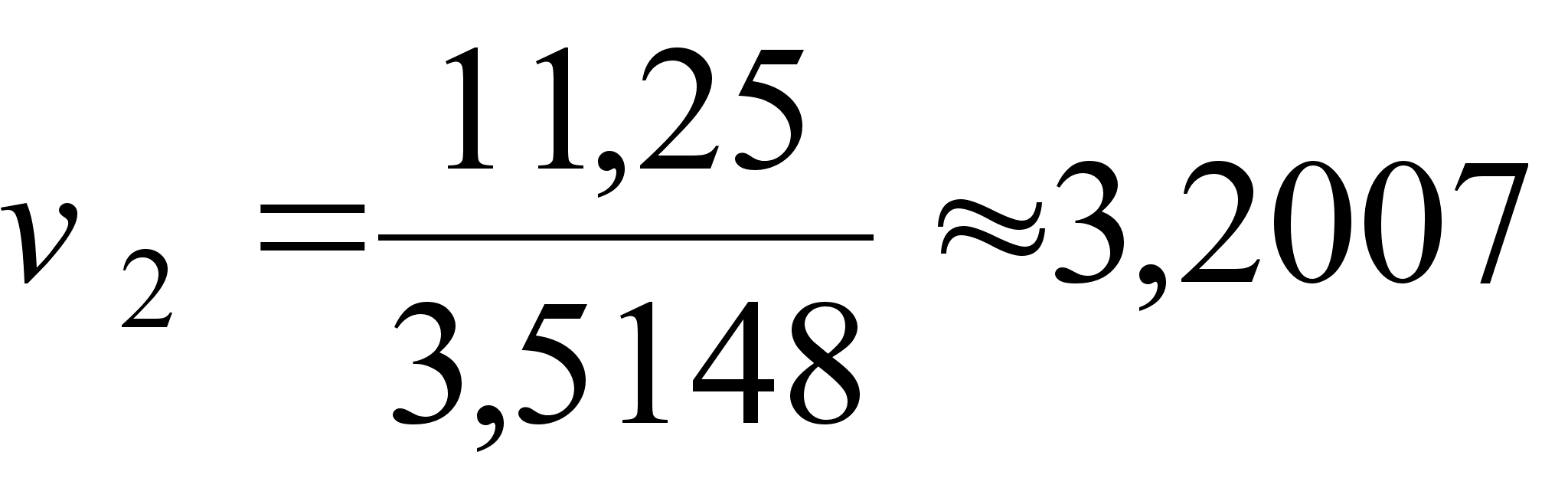при n
= 12;
– сравниваем
и 
с 
:
и 
.
Результаты
измерения Q1,11
и Q2,12
являются ошибочными,
они должны быть
отброшены.
Повторяем вычисления, при этом отбрасываем измерения №1-11 и №2-12:
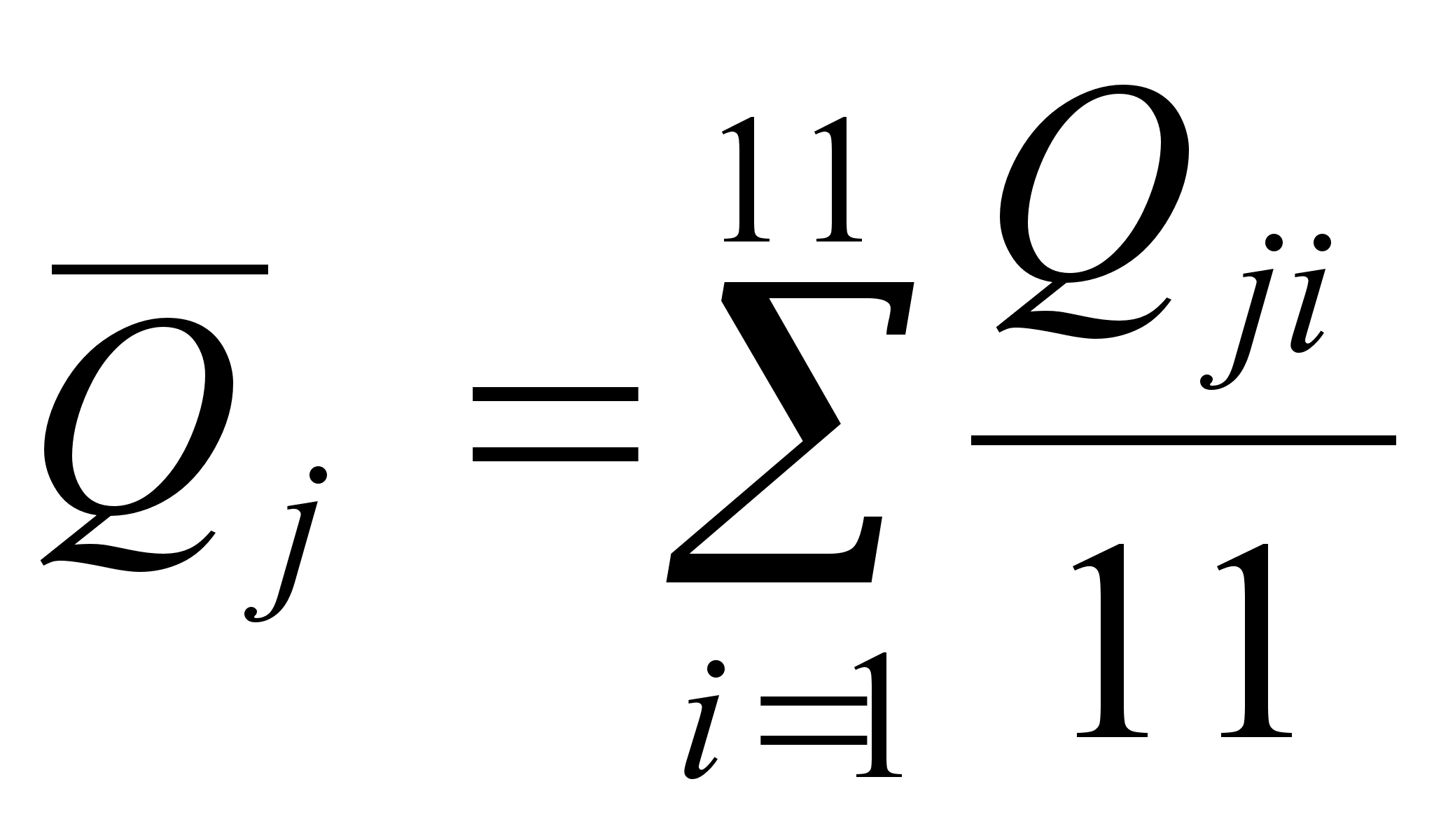(18)
(19)
Таблица 7
| Серия 1 | Серия 2 | ||||||
| № из-мерения | Результат измере-ния (Q1i) |
|
| № из-мерения | Результат измере-ния (Q2i) |
|
|
| 1 | 482 | -1,4545 | 2,1157 | 1 | 483 | 0,2727 | 0,0744 |
| 2 | 485 | 1,5455 | 2,3884 | 2 | 483 | 0,2727 | 0,0744 |
| 3 | 486 | 2,5455 | 6,4793 | 3 | 483 | 0,2727 | 0,0744 |
| 4 | 486 | 2,5455 | 6,4793 | 4 | 483 | 0,2727 | 0,0744 |
| 5 | 483 | -0,4545 | 0,2066 | 5 | 484 | 1,2727 | 1,6198 |
| 6 | 483 | -0,4545 | 0,2066 | 6 | 484 | 1,2727 | 1,6198 |
| 7 | 483 | -0,4545 | 0,2066 | 7 | 483 | 0,2727 | 0,0744 |
| 8 | 483 | -0,4545 | 0,2066 | 8 | 482 | -0,7273 | 0,5289 |
| 9 | 481 | -2,4545 | 6,0248 | 9 | 481 | -1,7273 | 2,9835 |
| 10 | 480 | -3,4545 | 11,9339 | 10 | 481 | -1,7273 | 2,9835 |
| 11 | 486 | 2,5455 | 6,4793 | 11 | 483 | 0,2727 | 0,0744 |
| Σ | 0 | 42,7273 | Σ | 0 | 10,1818 | ||
;
; 
;
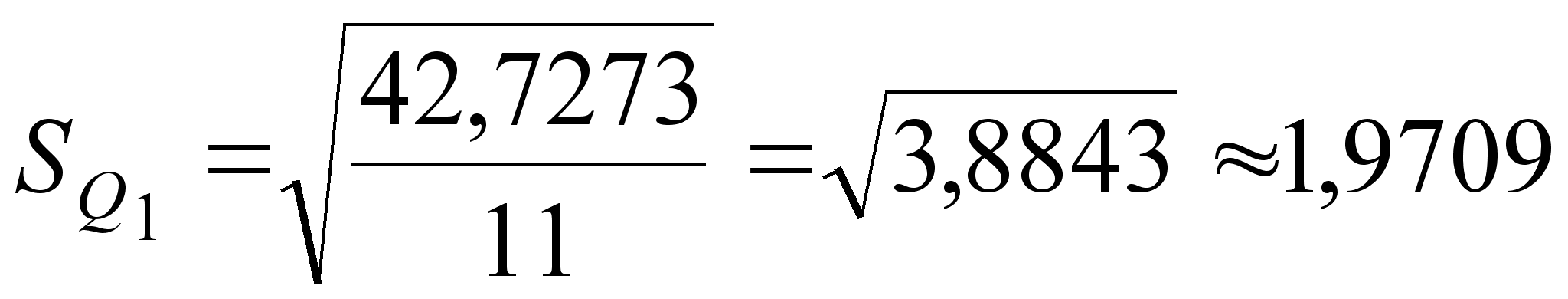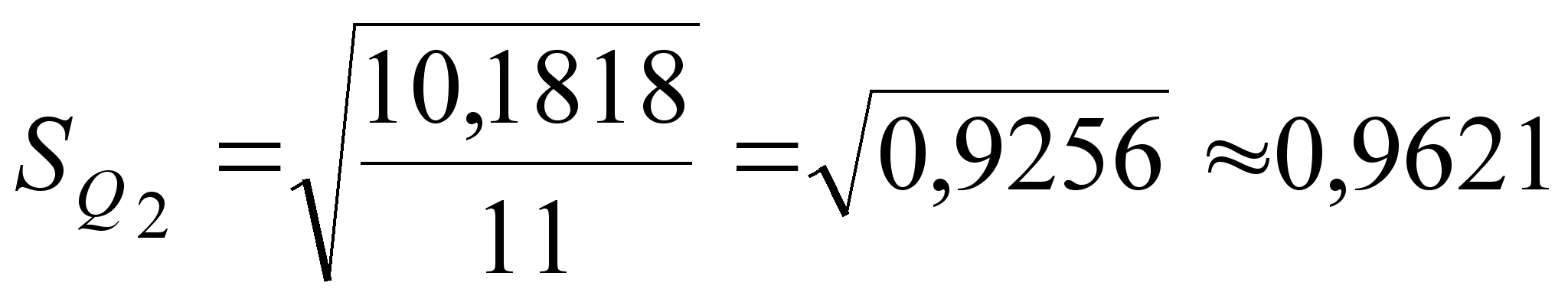
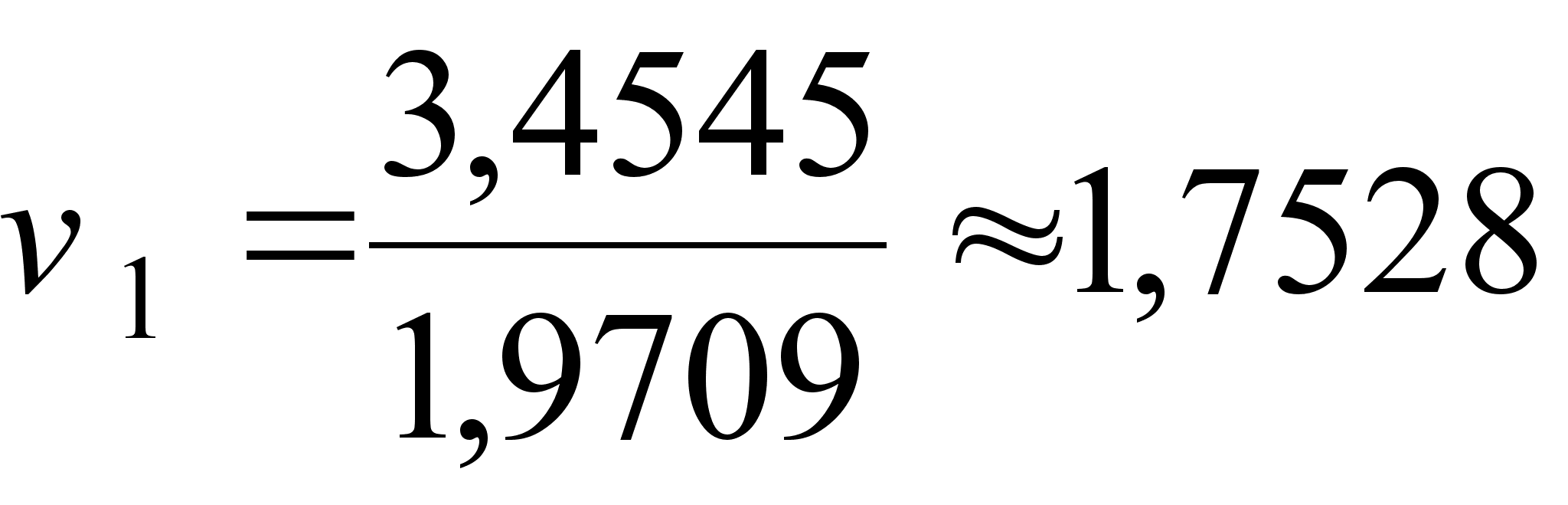при n
= 11;
Сравниваем
и
с :
и 
.
Результаты
измерений №1 10
и №2-9 не являются
ошибочными
и окончательно
остается 11 измерений
для обоих серий
измерений, т.е.
n
= 11.
– Так
как n
.
2. Проверяем значимость различия средних арифметических серий. Для этого:
– вычисляем моменты закона распределения разности:
, (21)
n1 = n2 = n
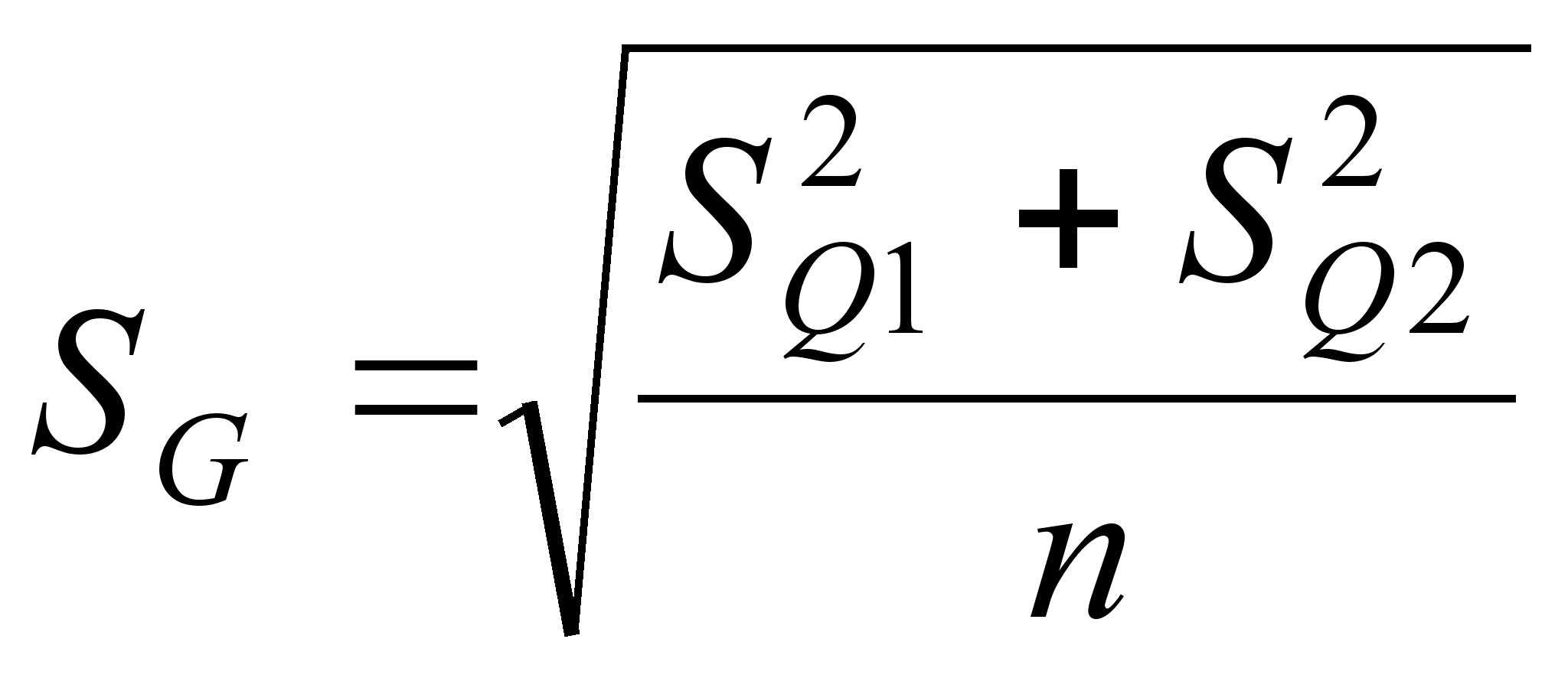(22)
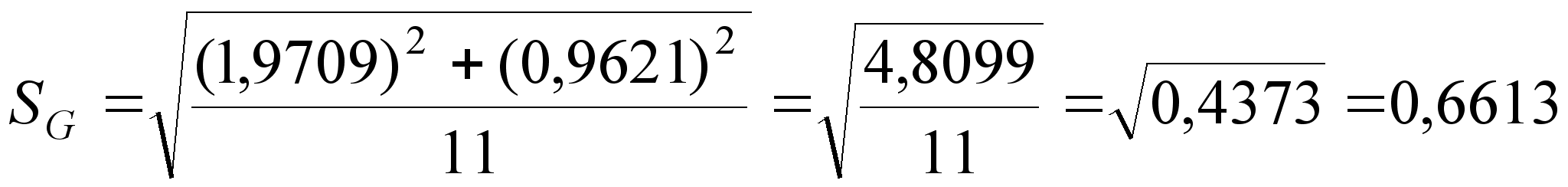
– задавшись доверительной вероятностью P = 0,95, определяем из таблицы интегральной функции нормированного нормального распределения Ф(t) значение t.
t = 1,645
– сравниваем
с 
,
.
.
Различия между
средними
арифметическими
в сериях с
доверительной
вероятностью
P
можно признать
незначимым
3. Проверим равнорассеянность результатов измерений в сериях, для этого:
– определяем значение Ψ:
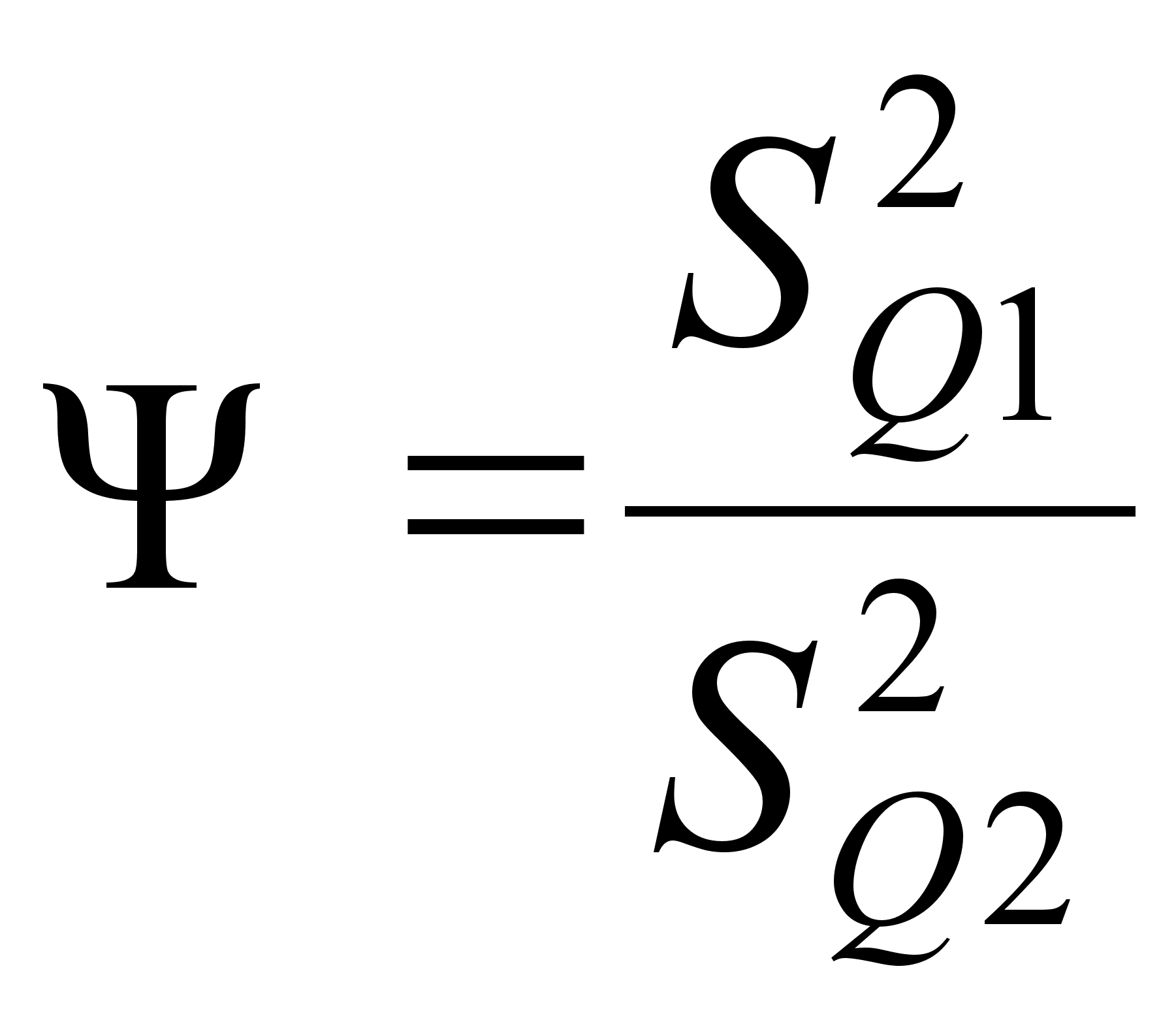(23)
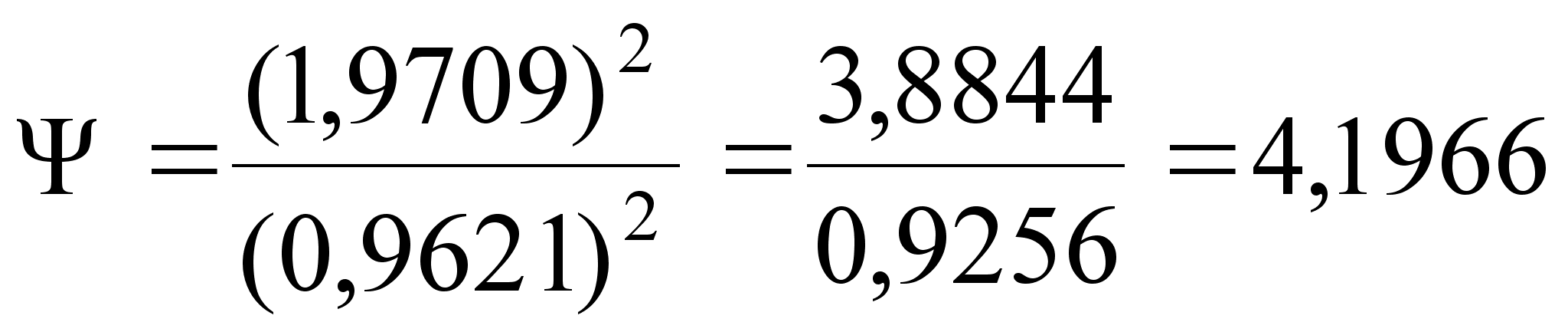> 1
Из таблицы находим значение аргумента интегральной функции распределения Фишера Ψ0; Ψ0=1,96 при P=0,95.
Сравниваем Ψ и Ψ0: Ψ > Ψ0, следовательно, серии с доверительной вероятностью P = 0,95 считаем рассеянными.
4. Обрабатываем совместно результаты измерения обеих серий с учетом весовых коэффициентов:
– определяем
оценки результата
измерения
и среднеквадратического
отклонения
S
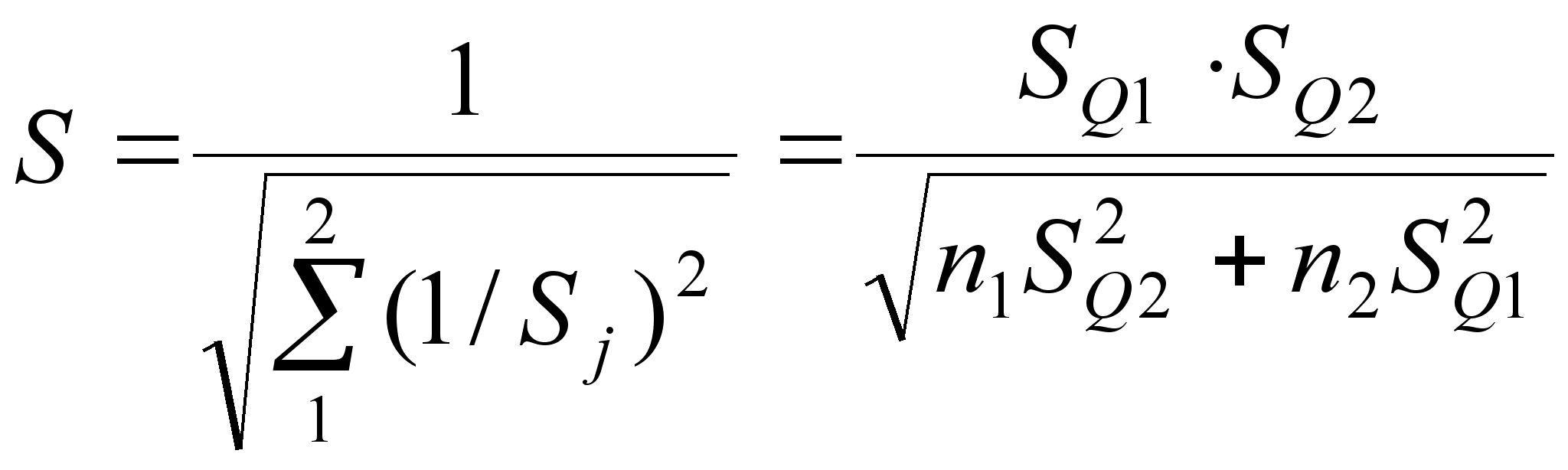(24)
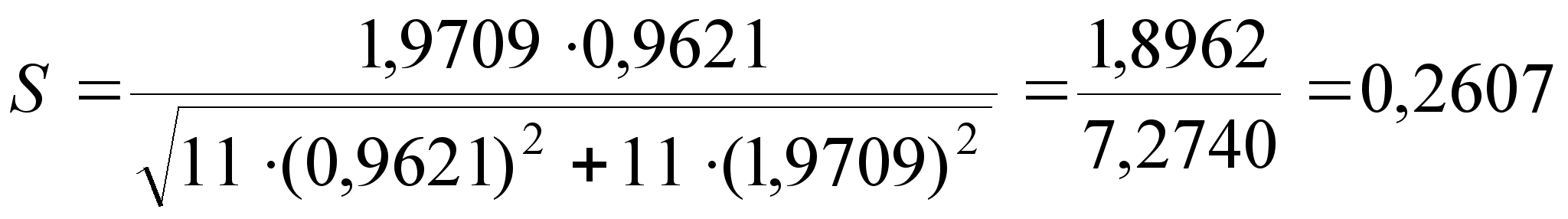
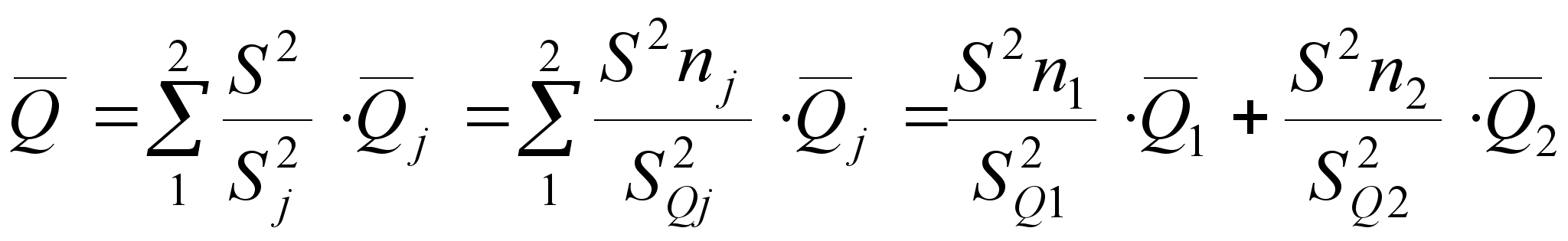(25)
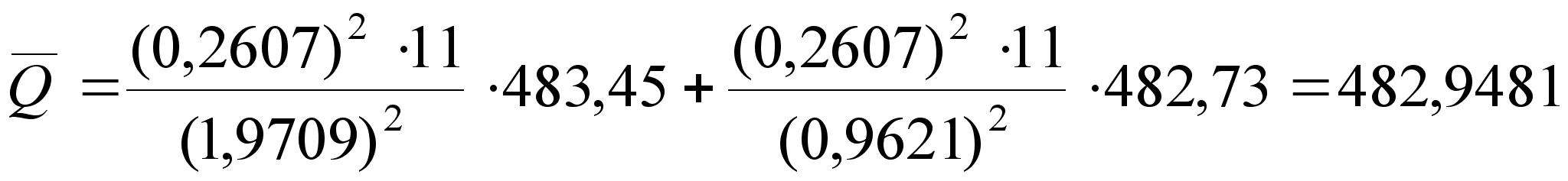
– задавшись доверительной вероятностью P = 0,95, определяем по таблице t = 1,96. Определяем доверительный интервал.
4. Функциональные преобразования результатов измерений (косвенные измерения)
Условие. При многократных измерениях независимых величин X и Y получено по 12 (n) результатов измерений. Эти результаты после внесения поправок представлены в таблице 8. Определить результат вычисления Z = f (X,Y).
Исходные данные:
Таблица 8
| Функция Z=f(X,Y) | № изме-рения | Значения величин | |||
| X – масса | Y – радиус сферы | ||||
| мкг | кг | мкм | м | ||
| плотность материала Z=3X/4πY3 | 1 | 482 | 4,82·10-7 | 483 | 4,83·10-4 |
| 2 | 485 | 4,85·10-7 | 483 | 4,83·10-4 | |
| 3 | 486 | 4,86·10-7 | 483 | 4,83·10-4 | |
| 4 | 486 | 4,86·10-7 | 483 | 4,83·10-4 | |
| 5 | 483 | 4,83·10-7 | 484 | 4,84·10-4 | |
| 6 | 483 | 4,83·10-7 | 484 | 4,84·10-4 | |
| 7 | 483 | 4,83·10-7 | 483 | 4,83·10-4 | |
| 8 | 483 | 4,83·10-7 | 482 | 4,82·10-4 | |
| 9 | 481 | 4,81·10-7 | 481 | 4,81·10-4 | |
| 10 | 480 | 4,80·10-7 | 481 | 4,81·10-4 | |
| 11 | 492 | 4,92·10-7 | 483 | 4,83·10-4 | |
| 12 | 486 | 4,86·10-7 | 495 | 4,95·10-4 | |
Расчет.
1. Обрабатываем экспериментальные данные по алгоритму, изложенному в п.п. 1–3 задания 2, при этом:
– определяем
оценки результатов
измерений 
,
и среднеквадратических
отклонений
и 
;
– обнаруживаем и исключаем ошибки;
– проверяем гипотезу о нормальности распределения оставшихся результатов измерений.
; 
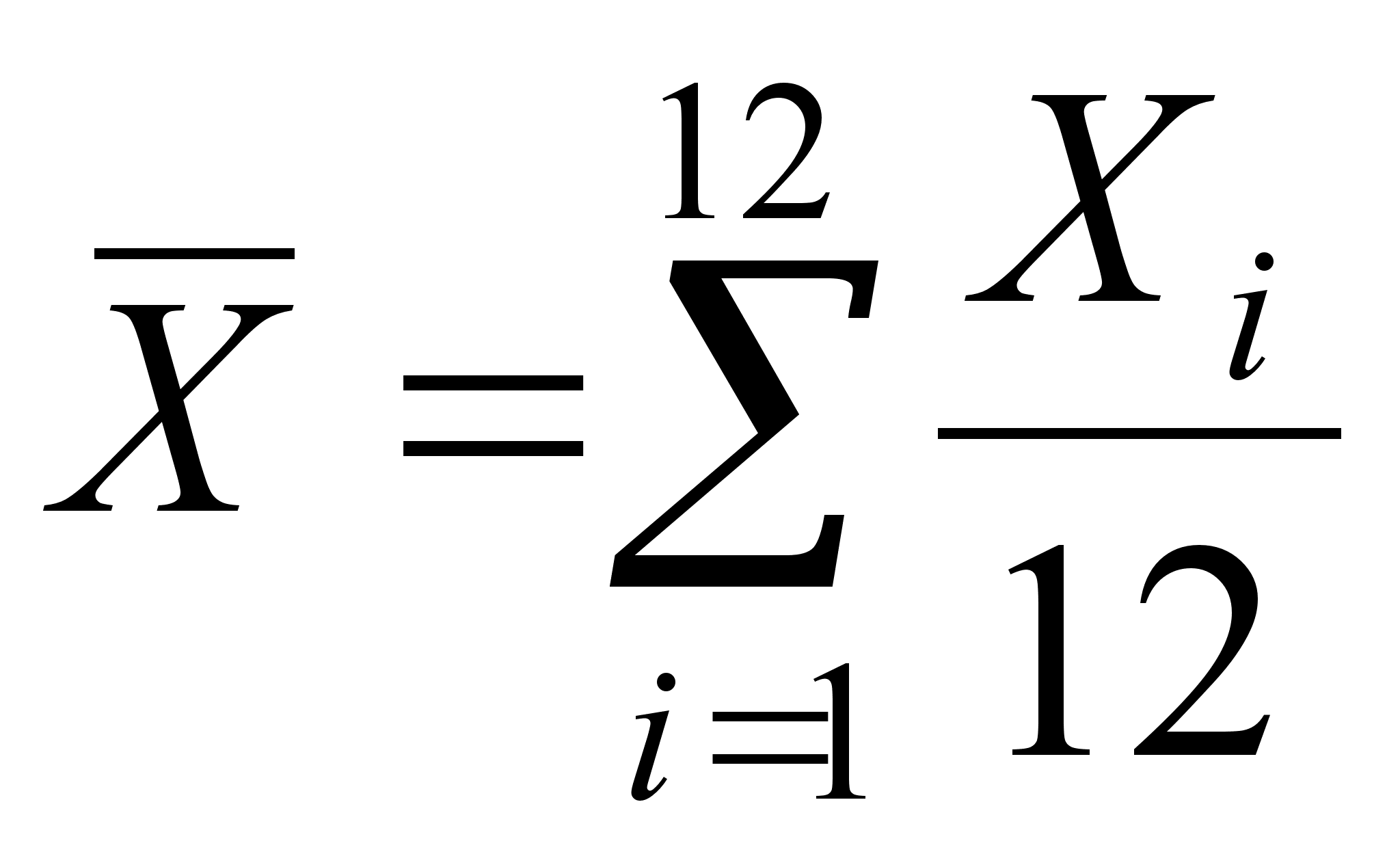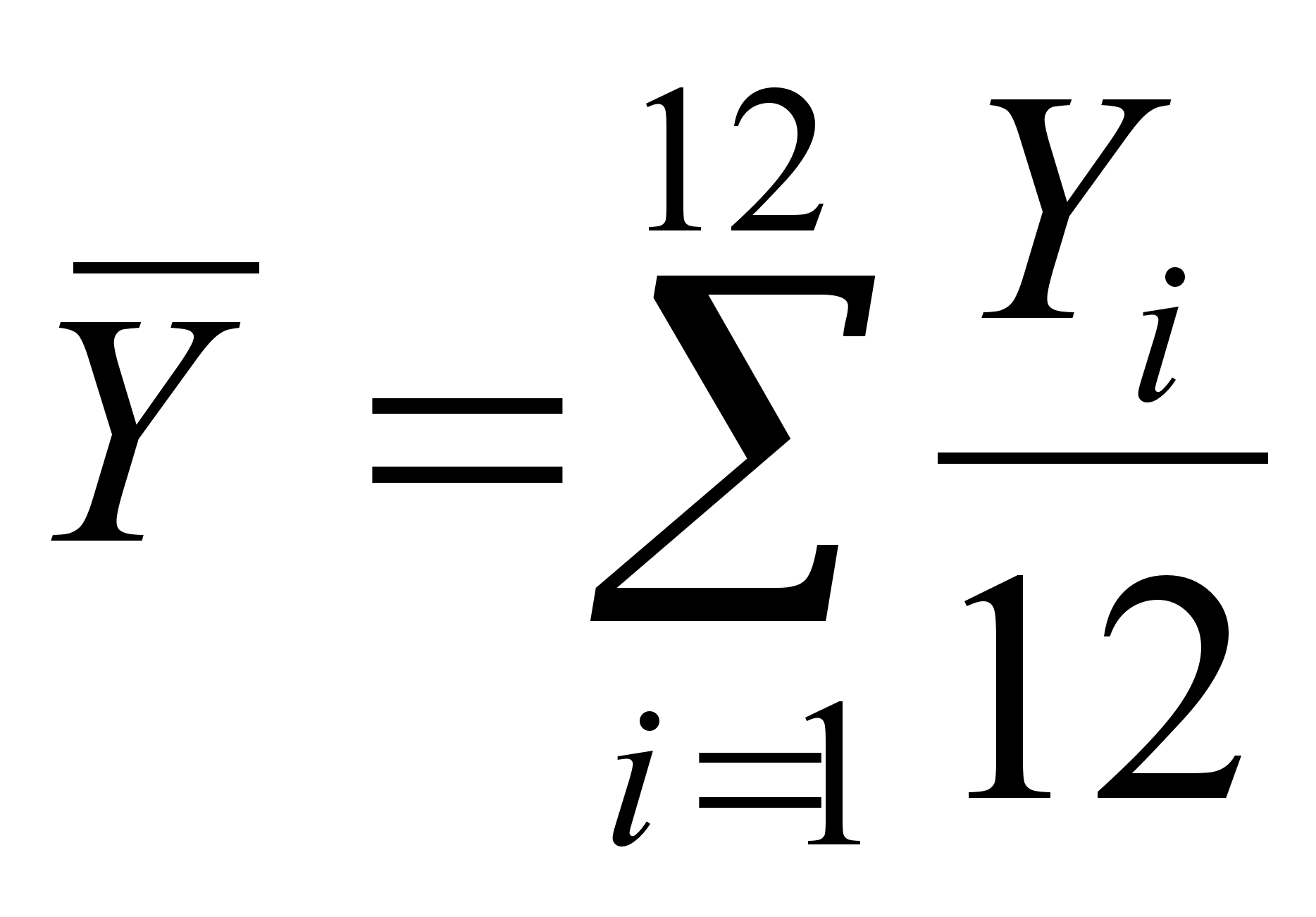(25)
; 
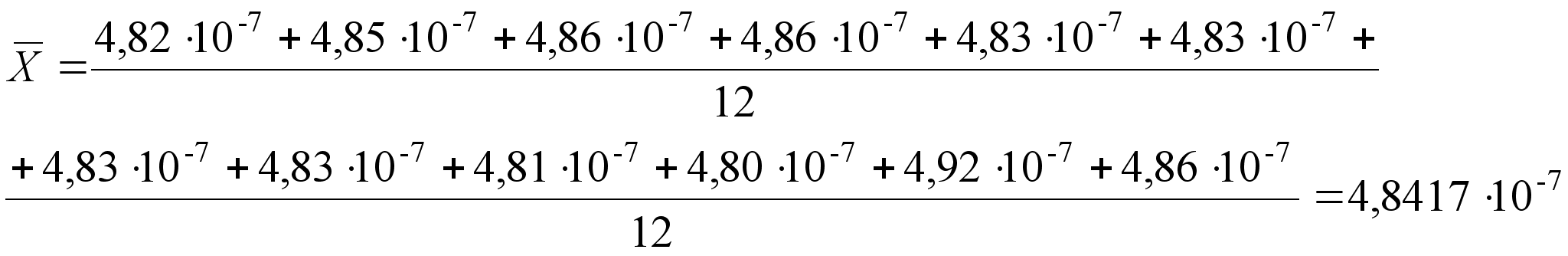
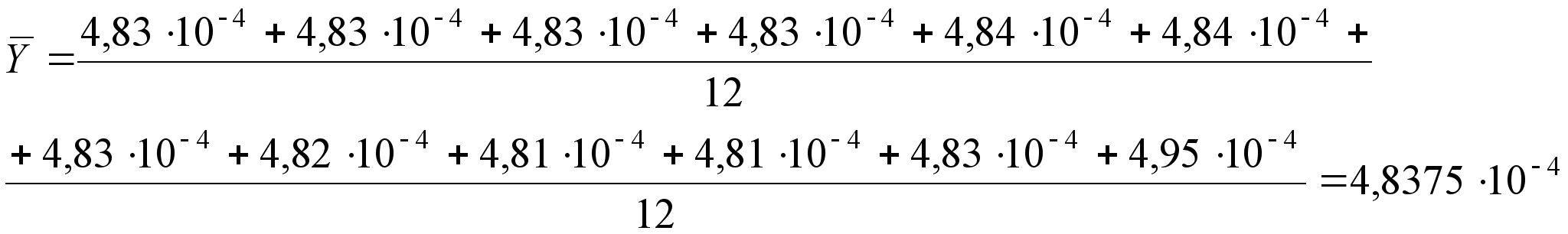
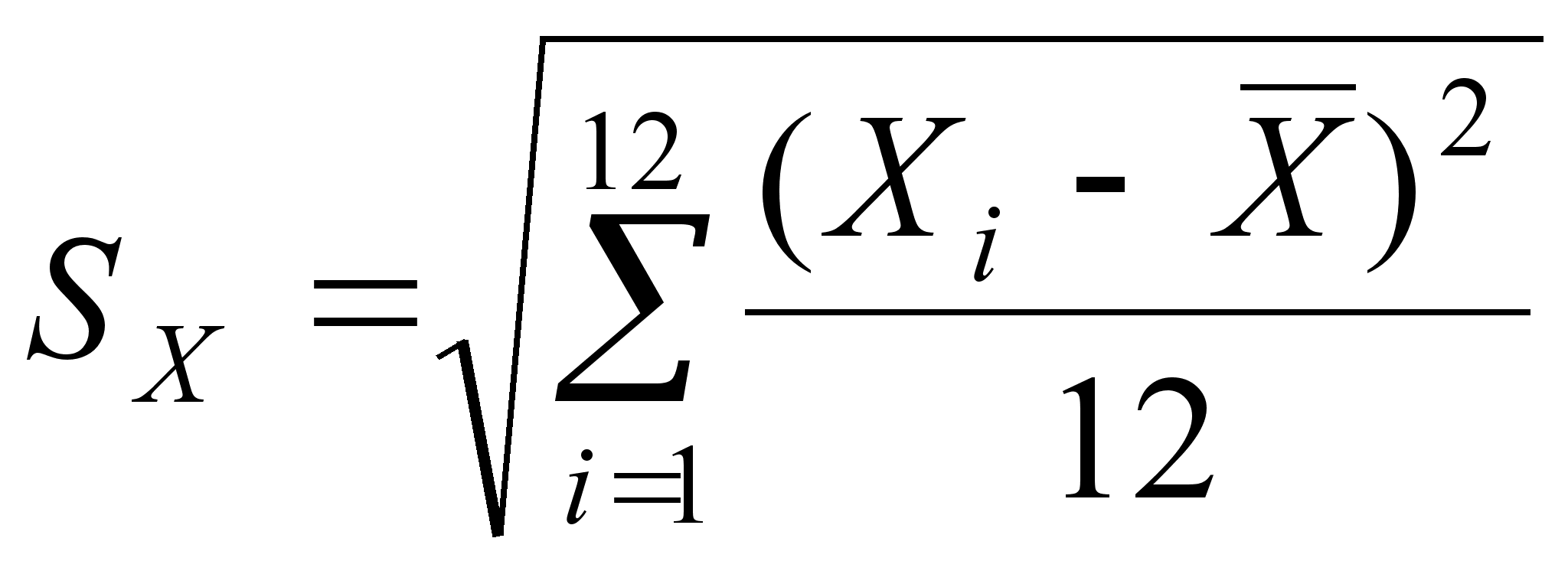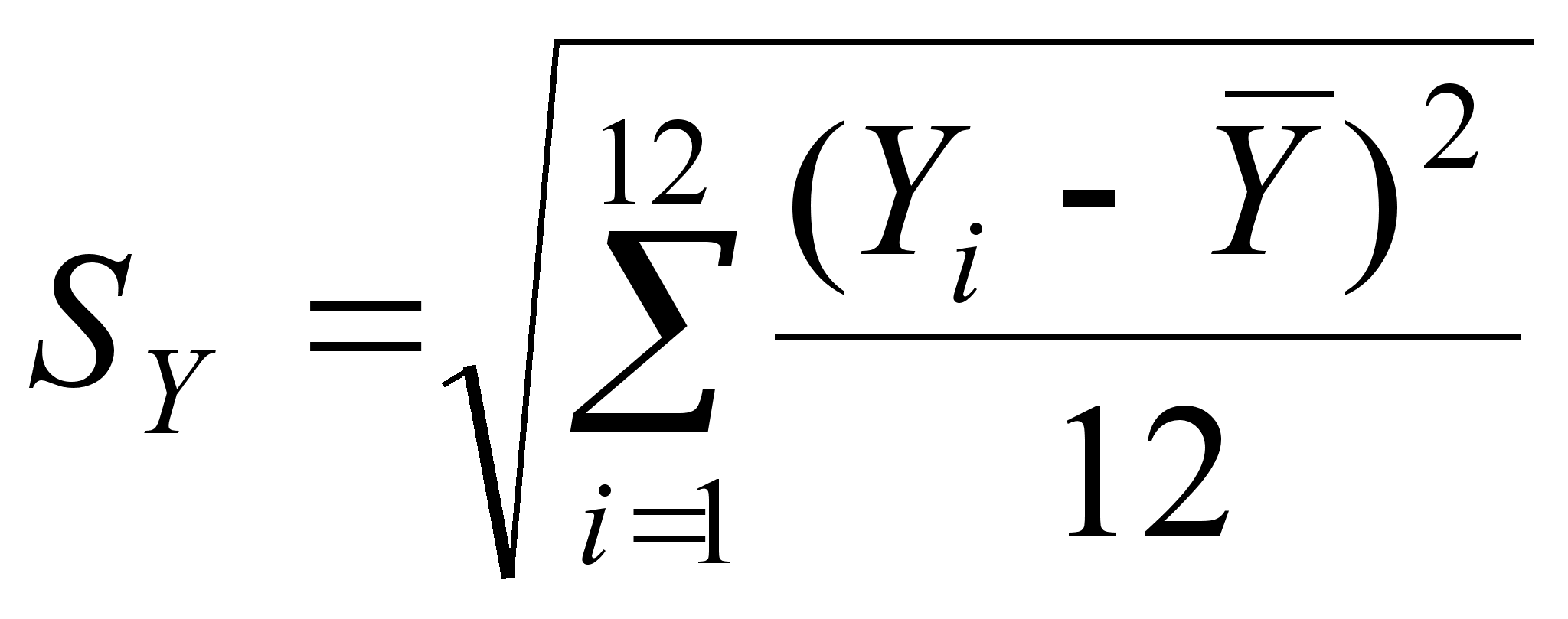(26)
Таблица 9
| Значения X | Значения Y | ||||||
| № из-мерения | Результат измере-ния (Xi) | | | № из-мерения | Результат измере-ния (Yi) |
| |
| 1 | 4,82·10-7 | -2,1667·10-9 | 4,6944·10-18 | 1 | 4,83·10-4 | -7,5·10-7 | 5,625·10-13 |
| 2 | 4,85·10-7 | 8,3333·10-10 | 6,9444·10-19 | 2 | 4,83·10-4 | -7,5·10-7 | 5,625·10-13 |
| 3 | 4,86·10-7 | 1,8333·10-9 | 3,3611·10-18 | 3 | 4,83·10-4 | -7,5·10-7 | 5,625·10-13 |
| 4 | 4,86·10-7 | 1,8333·10-9 | 3,3611·10-18 | 4 | 4,83·10-4 | -7,5·10-7 | 5,625·10-13 |
| 5 | 4,83·10-7 | -1,1667·10-9 | 1,3611·10-18 | 5 | 4,84·10-4 | 2,5·10-7 | 6,25·10-14 |
| 6 | 4,83·10-7 | -1,1667·10-9 | 1,3611·10-18 | 6 | 4,84·10-4 | 2,5·10-7 | 6,25·10-14 |
| 7 | 4,83·10-7 | -1,1667·10-9 | 1,3611·10-18 | 7 | 4,83·10-4 | -7,5·10-7 | 5,625·10-13 |
| 8 | 4,83·10-7 | -1,1667·10-9 | 1,3611·10-18 | 8 | 4,82·10-4 | -1,75·10-6 | 3,0625·10-12 |
| 9 | 4,81·10-7 | -3,1667·10-9 | 1,0028·10-17 | 9 | 4,81·10-4 | -2,75·10-6 | 7,5625·10-12 |
| 10 | 4,80·10-7 | -4,1667·10-9 | 1,7361·10-17 | 10 | 4,81·10-4 | -2,75·10-6 | 7,5625·10-12 |
| 11 | 4,92·10-7 | 7,8333·10-9 | 6,1361·10-17 | 11 | 4,83·10-4 | -7,5·10-7 | 5,625·10-13 |
| 12 | 4,86·10-7 | 1,8333·10-9 | 3,3611·10-18 | 12 | 4,95·10-4 | 1,125·10-5 | 1,2656·10-10 |
| Σ | 0 | 1,0967·10-16 | Σ | 0 | 1,4825·10-10 | ||
;
;
; 
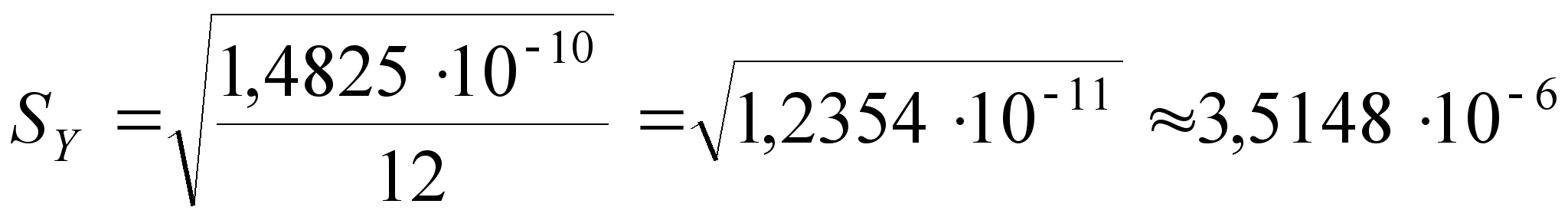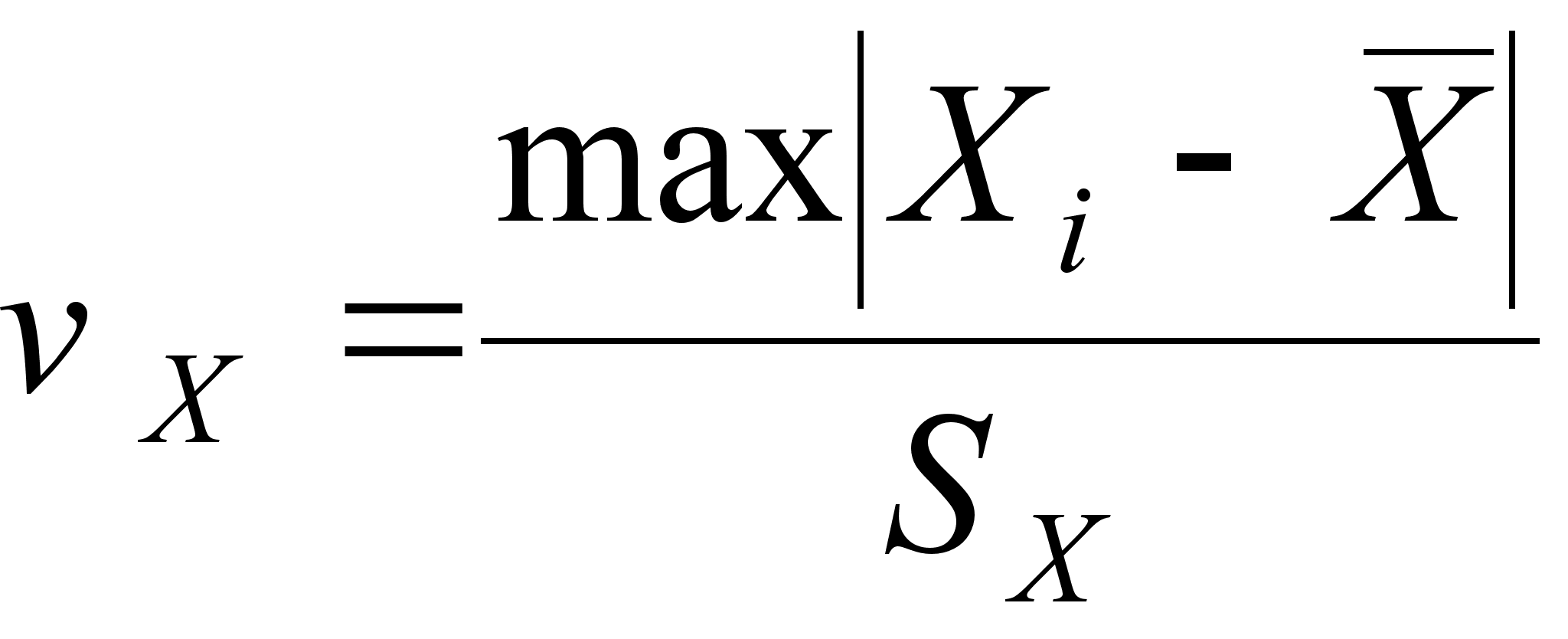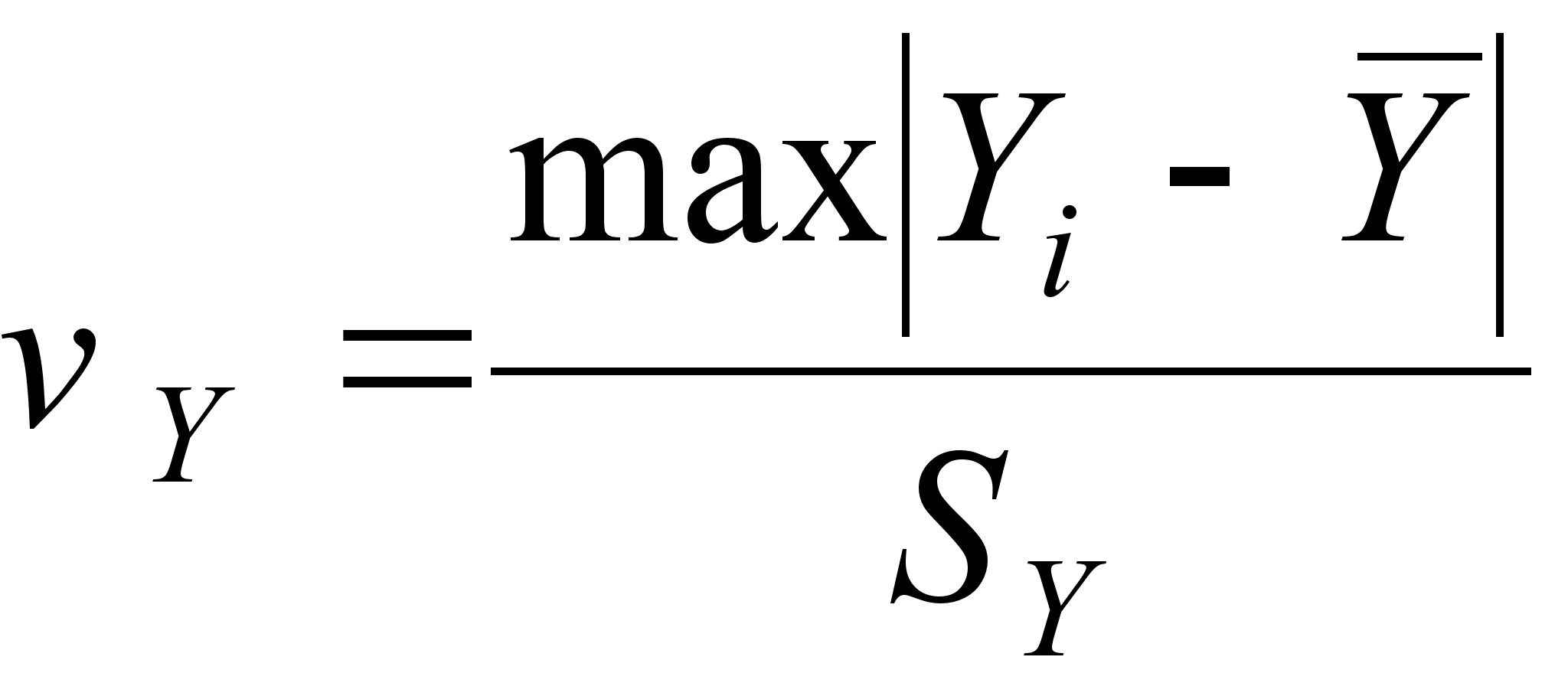(27)
; 
;
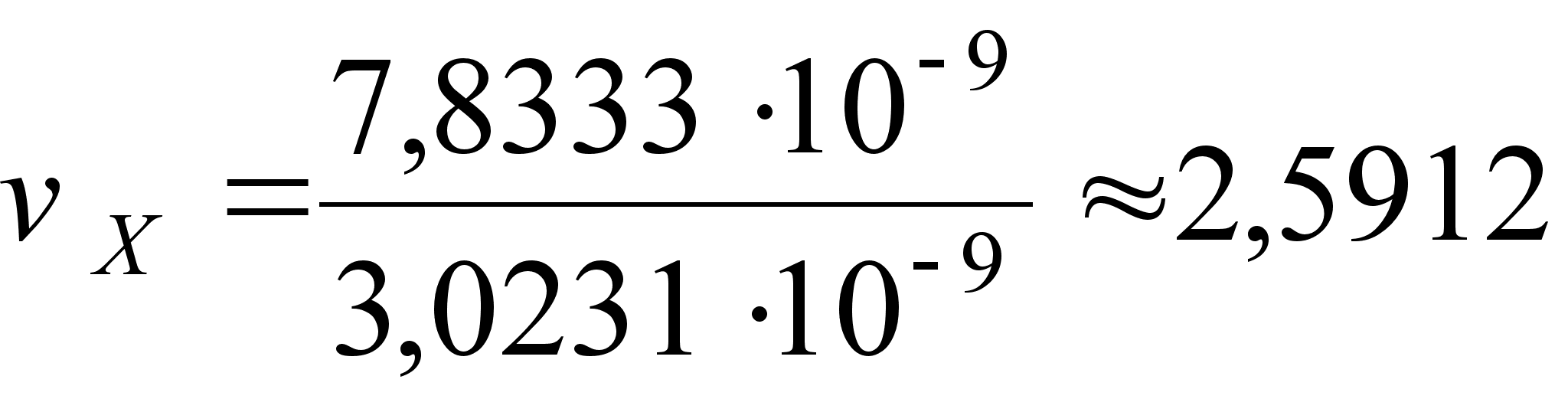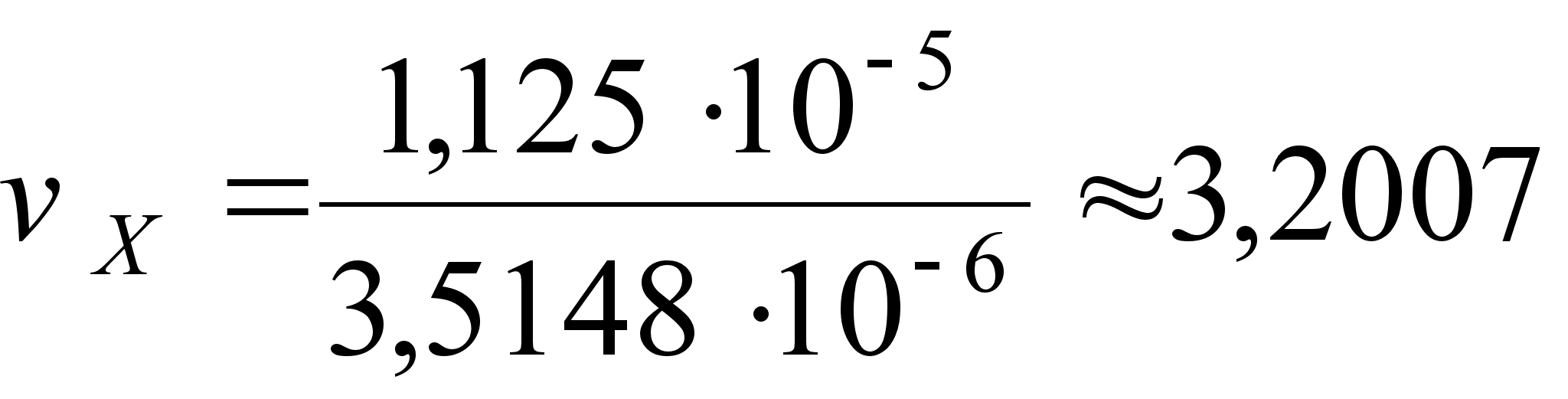при n
= 12;
– сравниваем
и 
с :
и 
.
Результаты
измерения X11
и Y12
являются ошибочными,
они должны быть
отброшены.
Повторяем вычисления, при этом отбрасываем измерения X11 и Y12:
Таблица 10
| Значения X | Значения Y | ||||||
| № из-мерения | Результат измере-ния (Xi) | | | № из-мерения | Результат измере-ния (Yi) |
| |
| 1 | 4,82·10-7 | -1,4545·10-9 | 2,1157·10-18 | 1 | 4,83·10-4 | 2,7273·10-7 | 0,07438·10-14 |
| 2 | 4,85·10-7 | 1,5455·10-9 | 2,3884·10-18 | 2 | 4,83·10-4 | 2,7273·10-7 | 0,07438·10-14 |
| 3 | 4,86·10-7 | 2,5455·10-9 | 6,4793·10-18 | 3 | 4,83·10-4 | 2,7273·10-7 | 0,07438·10-14 |
| 4 | 4,86·10-7 | 2,5455·10-9 | 6,4793·10-18 | 4 | 4,83·10-4 | 2,7273·10-7 | 0,07438·10-14 |
| 5 | 4,83·10-7 | -4,5455·10-10 | 2,0661·10-19 | 5 | 4,84·10-4 | 1,2727·10-6 | 1,6198·10-12 |
| 6 | 4,83·10-7 | -4,5455·10-10 | 2,0661·10-19 | 6 | 4,84·10-4 | 1,2727·10-6 | 1,6198·10-12 |
| 7 | 4,83·10-7 | -4,5455·10-10 | 2,0661·10-19 | 7 | 4,83·10-4 | 2,7273·10-7 | 0,07438·10-14 |
| 8 | 4,83·10-7 | -4,5455·10-10 | 2,0661·10-19 | 8 | 4,82·10-4 | -7,2727·10-7 | 5,2893·10-13 |
| 9 | 4,81·10-7 | -2,4545·10-9 | 6,0248·10-18 | 9 | 4,81·10-4 | -1,7273·10-6 | 2,9835·10-12 |
| 10 | 4,80·10-7 | -3,4545·10-9 | 1,1934·10-17 | 10 | 4,81·10-4 | -1,7273·10-6 | 2,9835·10-12 |
| 11 | 4,86·10-7 | 2,5455·10-9 | 6,4793·10-18 | 11 | 4,83·10-4 | 2,7273·10-7 | 0,07438·10-14 |
| Σ | 0 | 4,2727·10-17 | Σ | 0 | 1,0182·10-11 | ||
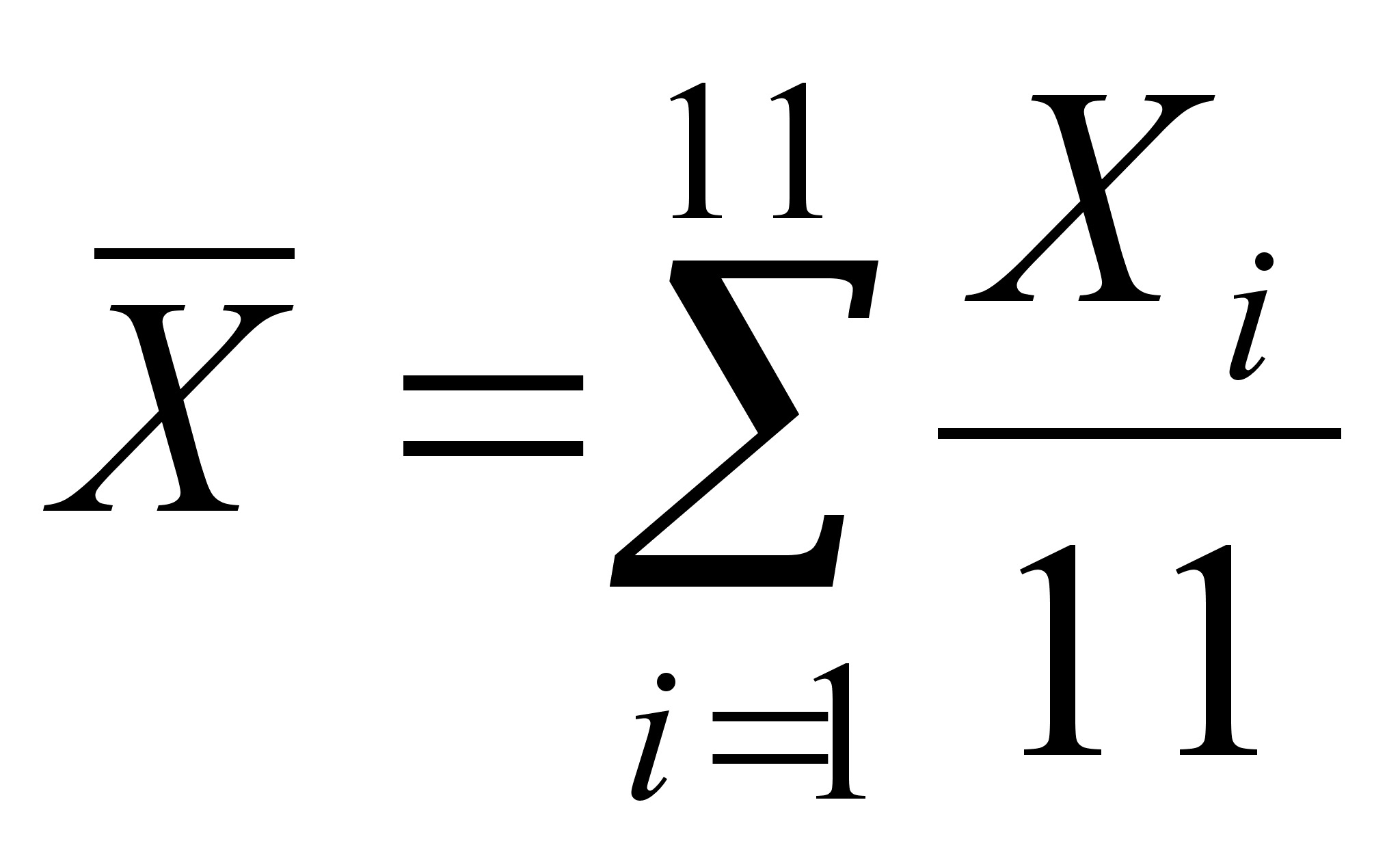
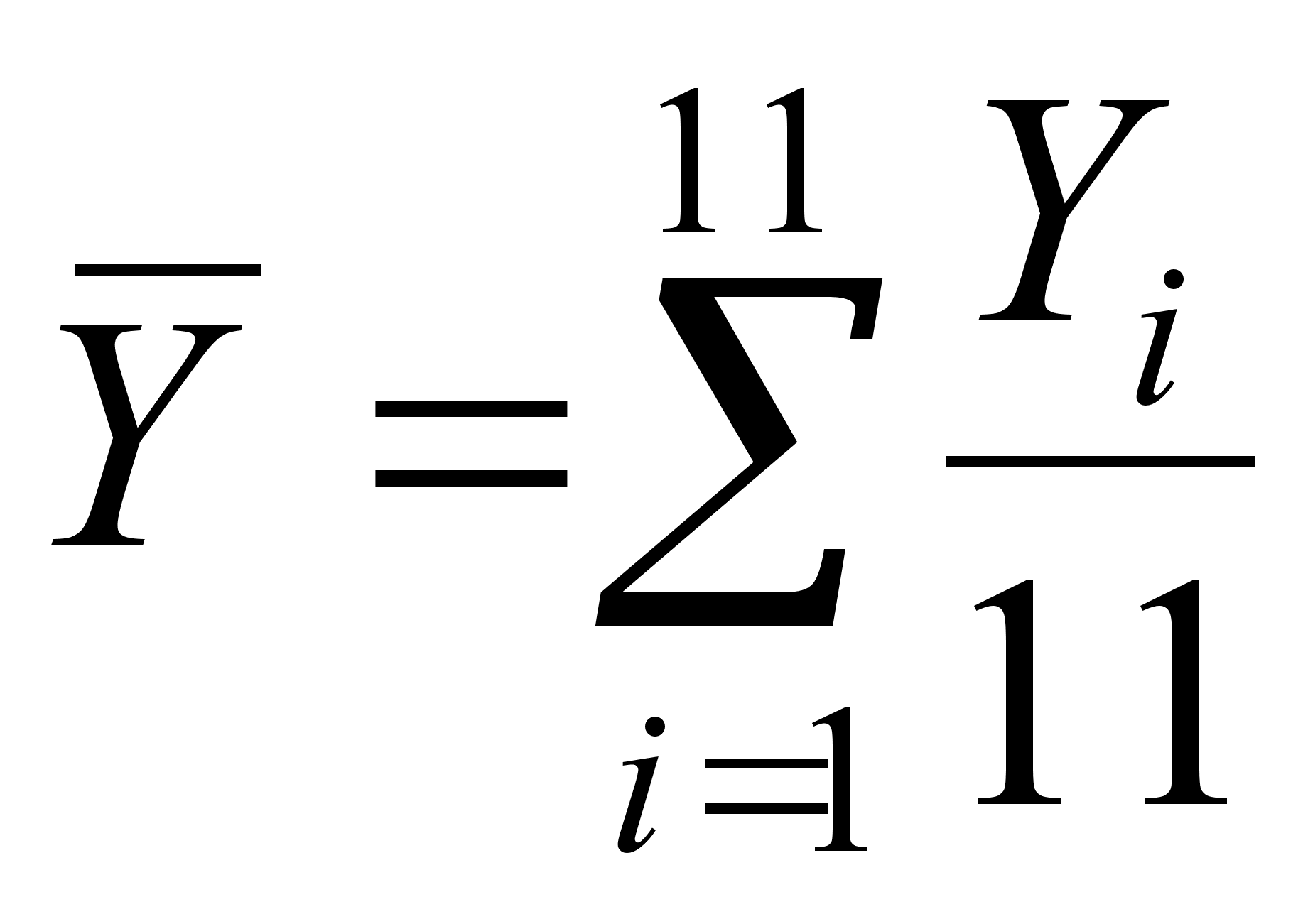(28)
;
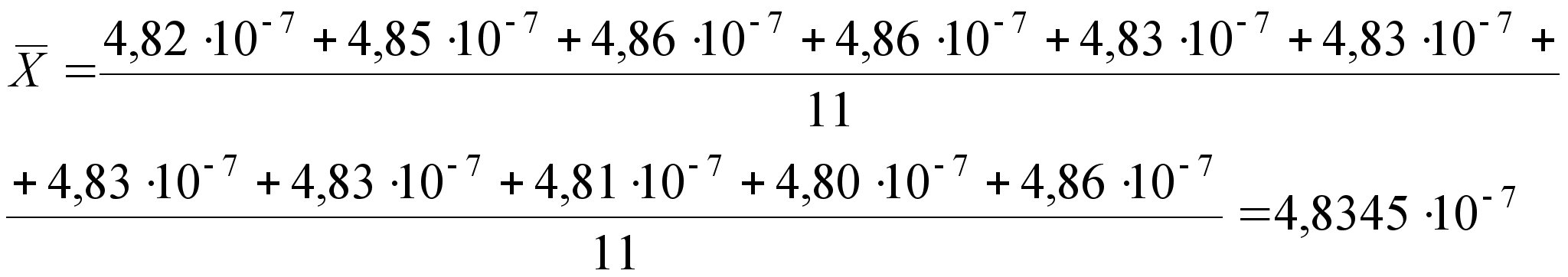
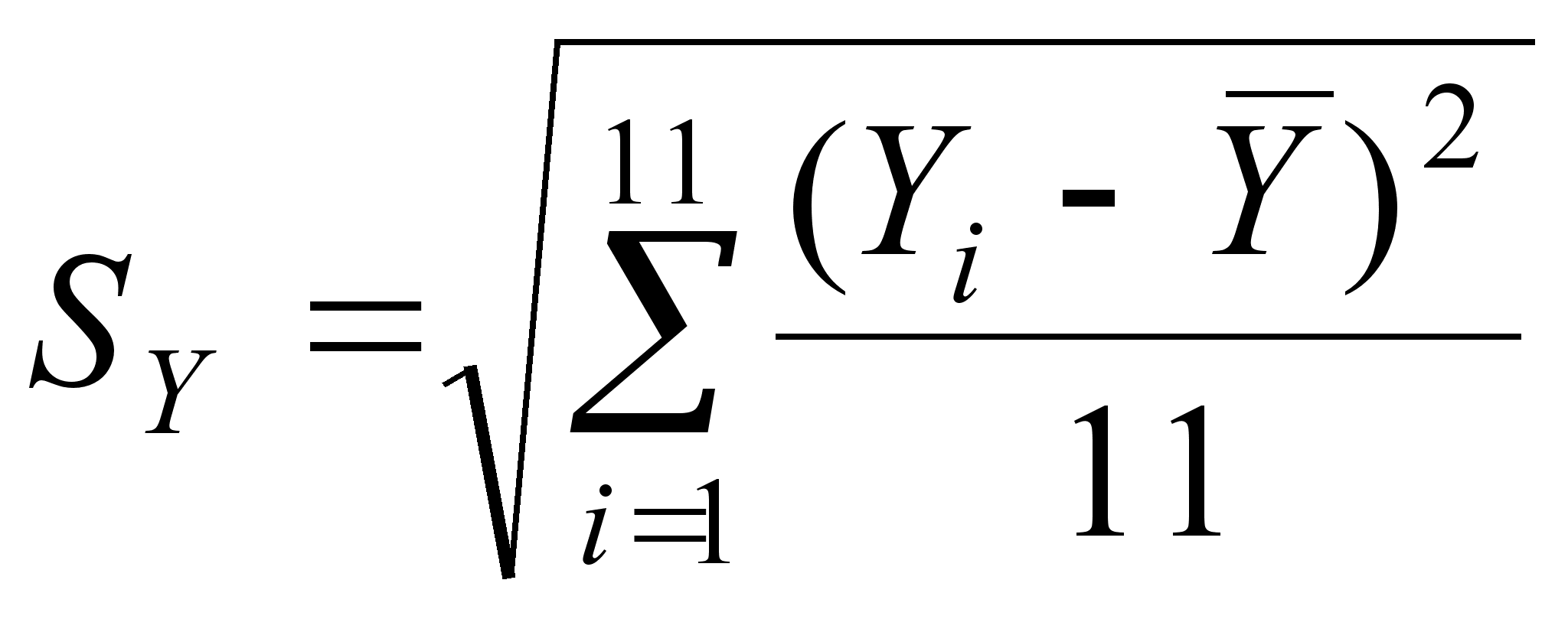(29)
;
; 
;
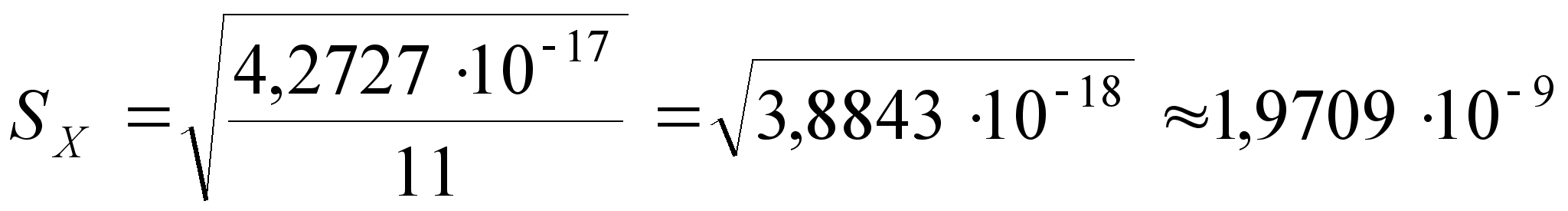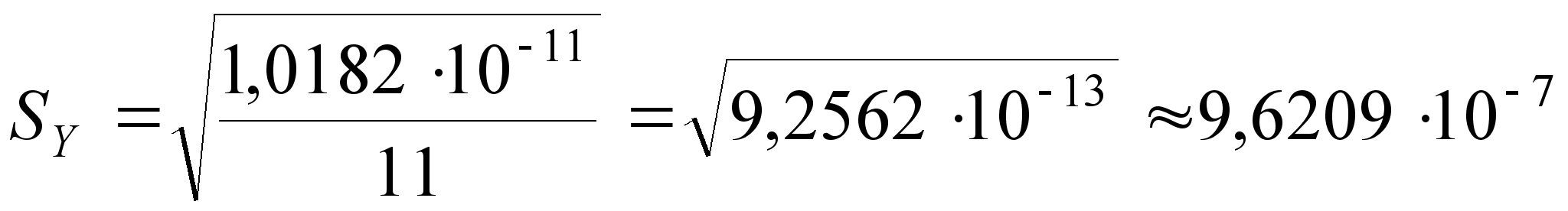
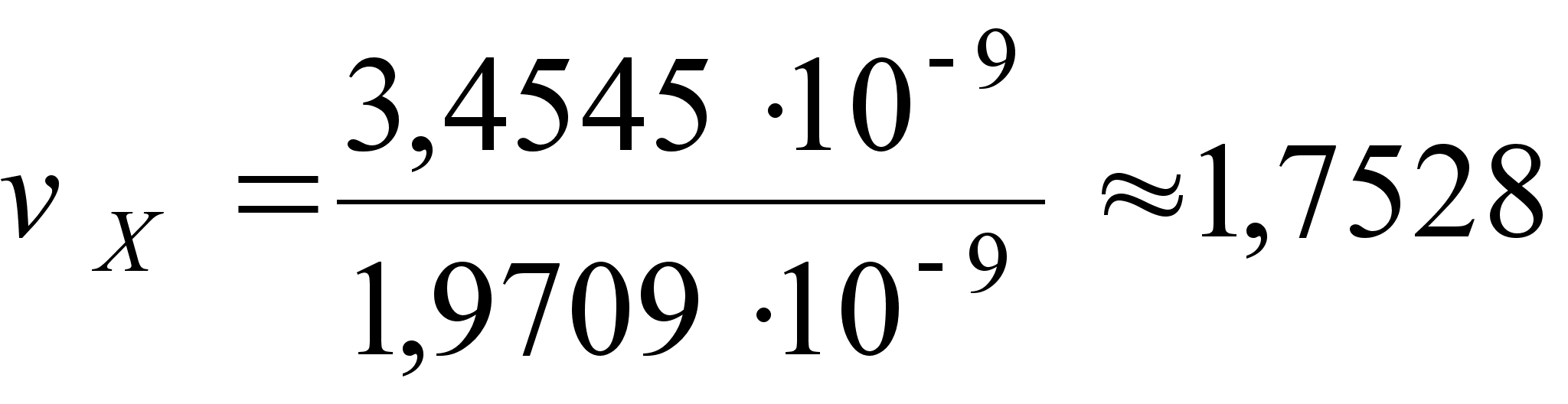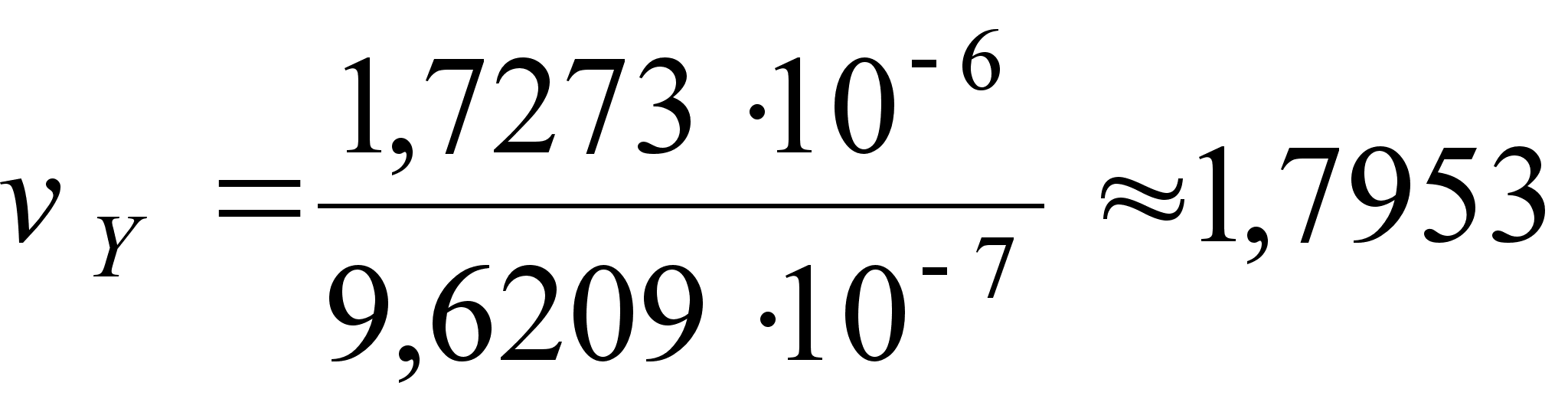при n
= 11;
Сравниваем
и
с :
и 
.
Результаты
измерений X10
и Y9
не являются
ошибочными
и окончательно
остается 11 измерений
для обоих видов
величин измерений,
т.е. n
= 11.
Так как
n
.
2. Определяем оценку среднего значения функции
; (30)
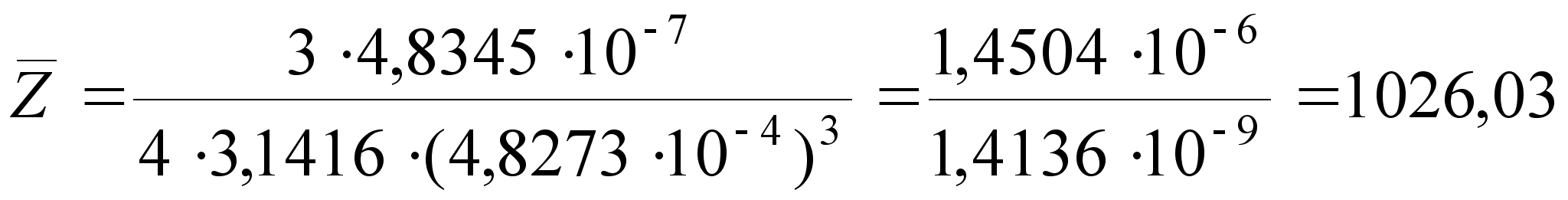
3. Находим частные производные первого и второго порядка для функции Z = f (X,Y) по X и Y.
;
;
;
;
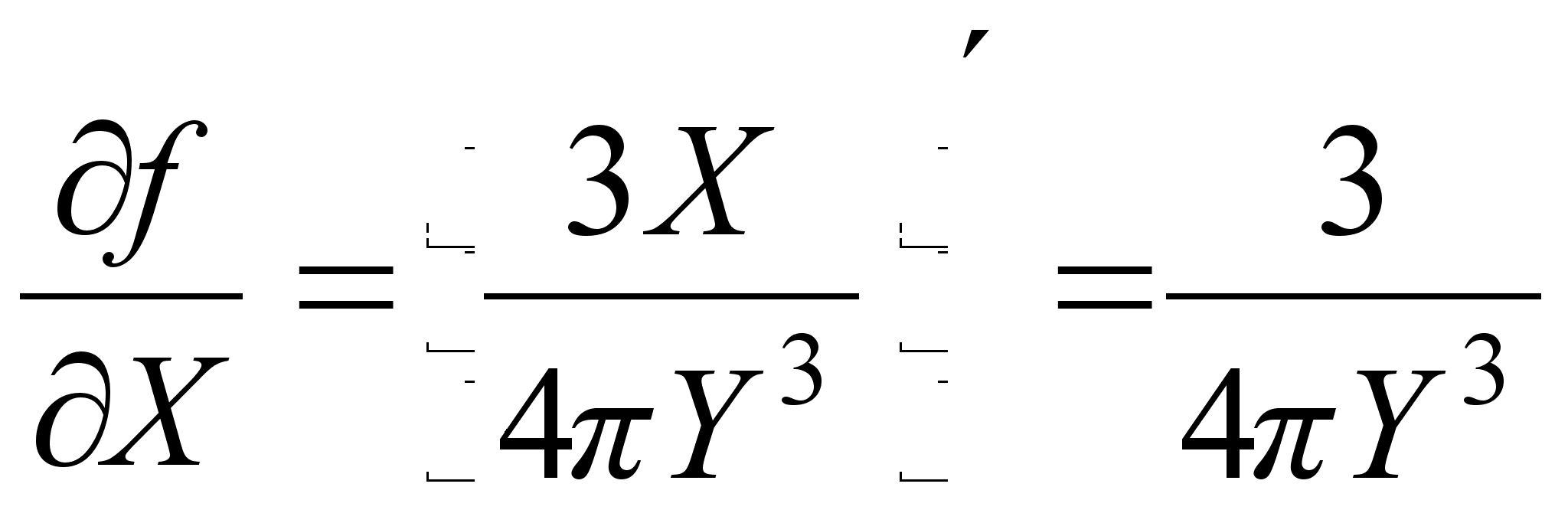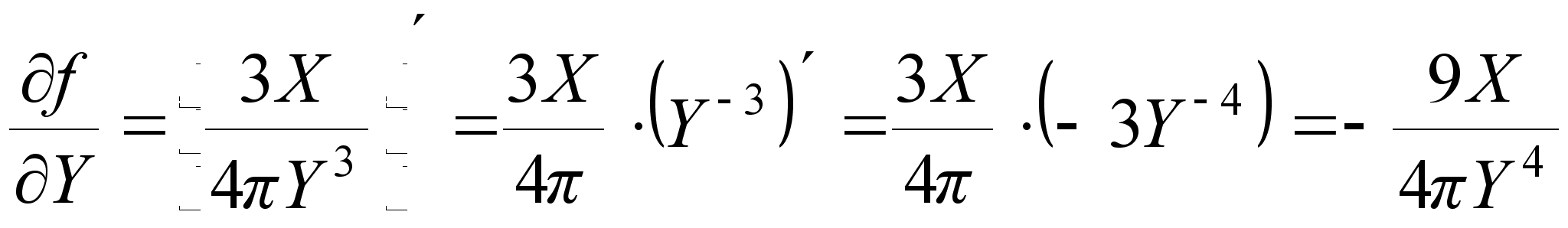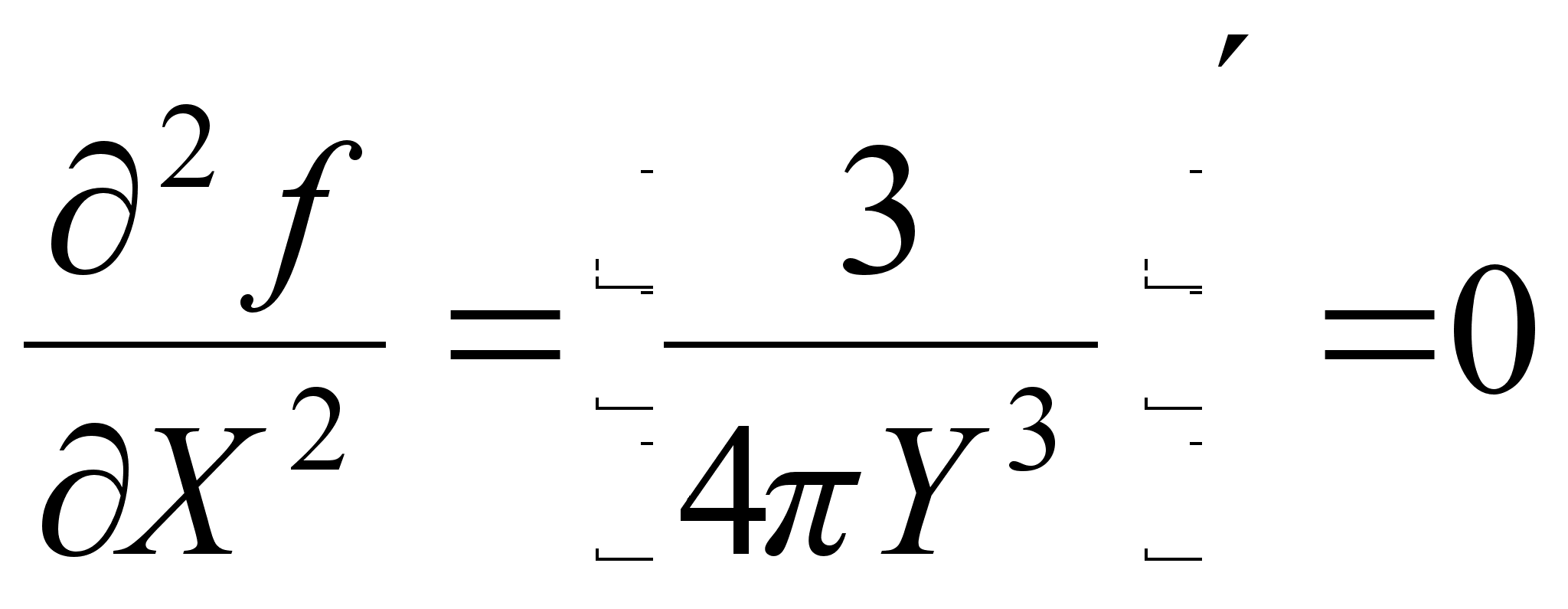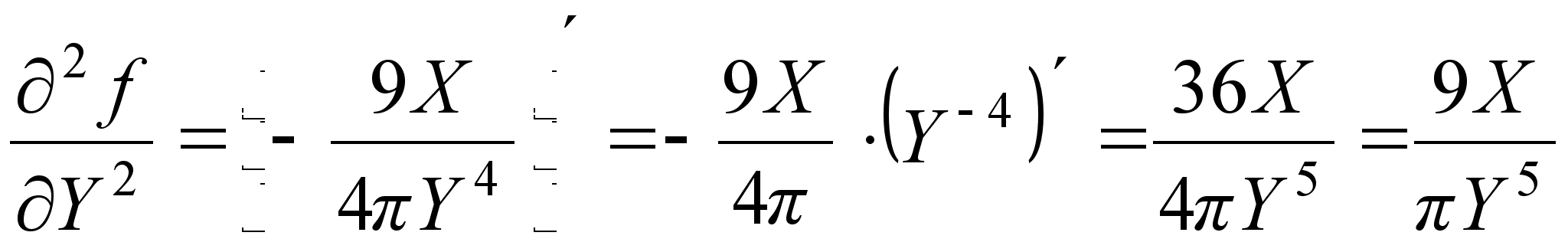Определяем поправку:
(31)
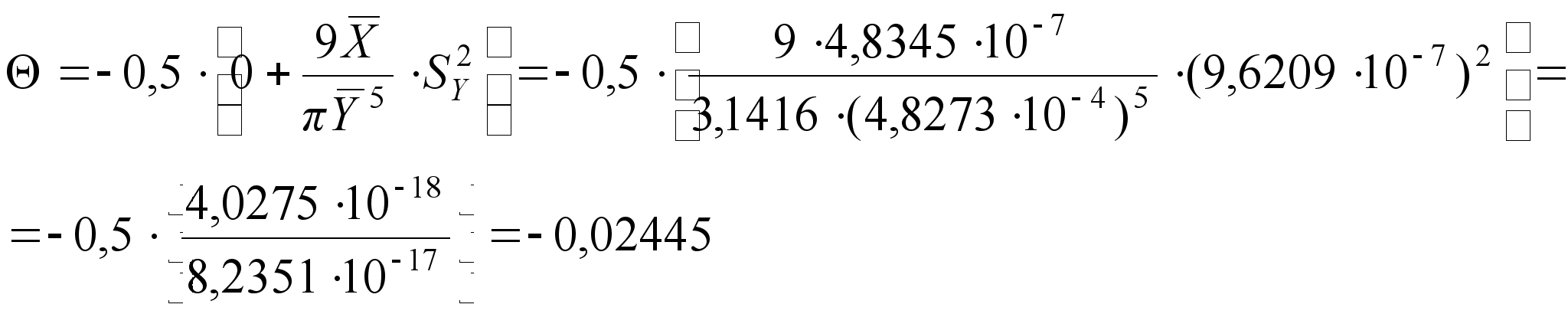
Похожие работы
... вывод, что случайная величина распределена по равномерному закону, а случайная величина – по нормальному. Заключение В ходе курсовой работы были освоены методы обработки данных статистического наблюдения, их анализа с помощью обобщающих показателей, установление теоретических законов распределения случайных величин и доказательство адекватности этих законов. Также в результате выполнения ...
... называется группа упорядоченных по величине значений признака, заменяемая в процессе расчетов средним значением. 2. Методы вторичной статистической обработки результатов эксперимента С помощью вторичных методов статистической обработки экспериментальных данных непосредственно проверяются, доказываются или опровергаются гипотезы, связанные с экспериментом. Эти методы, как правило, сложнее, ...
... снятия вклада на межмолекулярные взаимодействия рассчитывалась бессимметрийная газофазная константа равновесия реакции . Давления насыщенного пара рассчитывались методом Ли-Кеслера [50] или по экспериментальным данным. Применение к расчету давлений насыщенного пара методики, описанной в главе 2.1, позволяет обеспечить погрешность расчета не более 10% отн. для всех давлений, приведенных в данной ...
... проведении физического эксперимента. Простота же общения дала возможность неквалифицированному исследователю принимать участие в серьёзных научных проектах. Именно для него, по-видимому, и были созданы пакеты обработки экспериментальных данных SABR и BOOTSTRAP, позволяющие находить зависимость физических величин по экспериментальным данным с большой достоверностью не только при неизвестном законе ...
0 комментариев