Определяем оценку стандартного отклонения функции

4. Определяем оценку стандартного отклонения функции

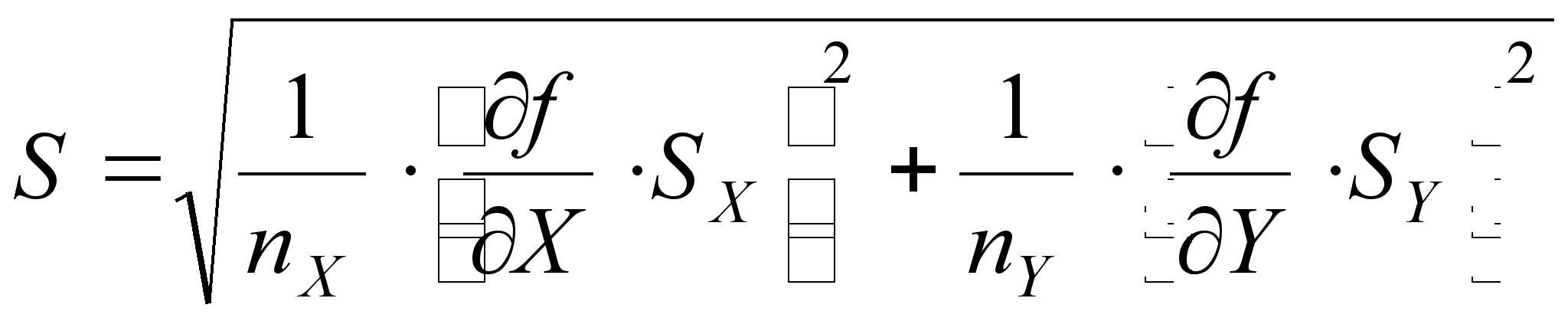(32)

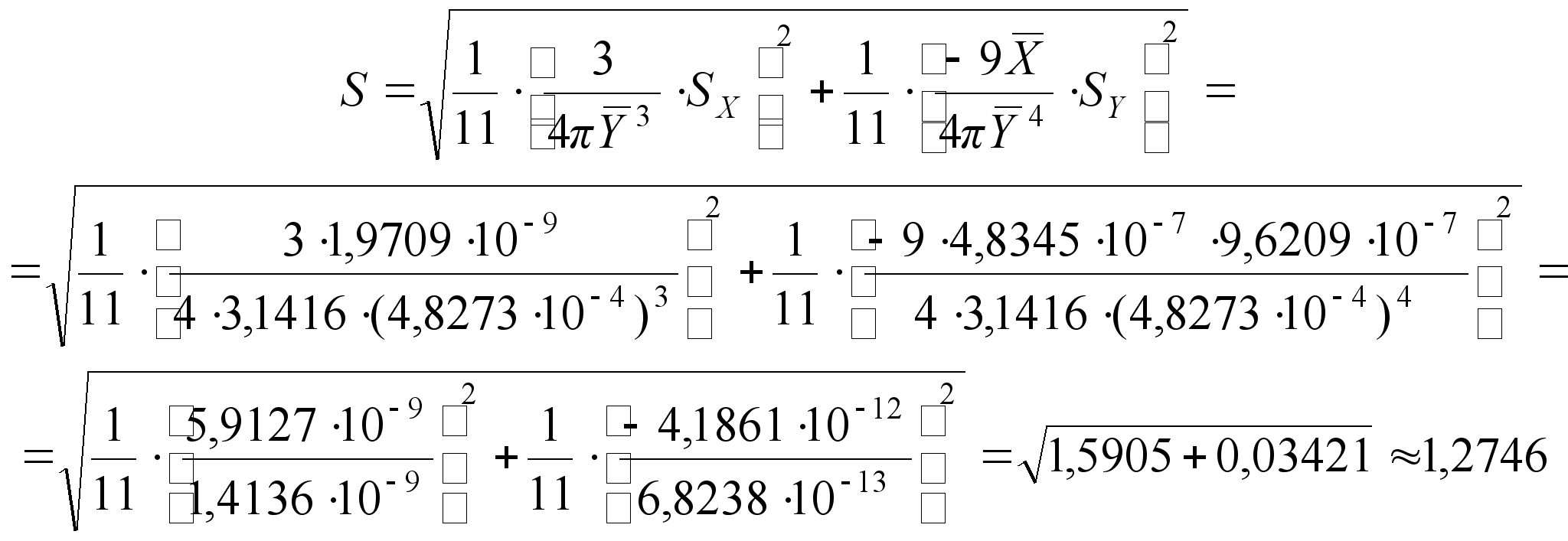
5. Находим число степеней свободы

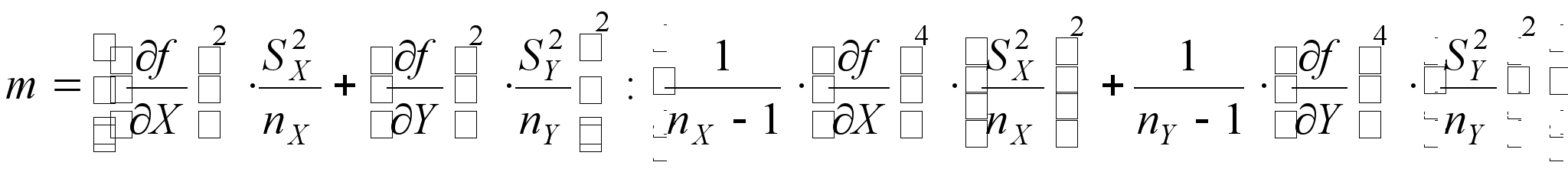(33)

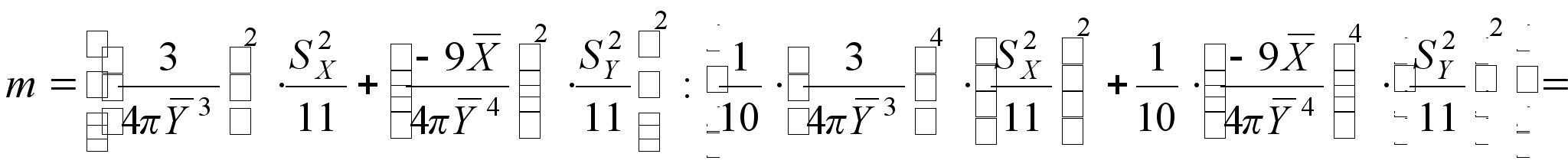
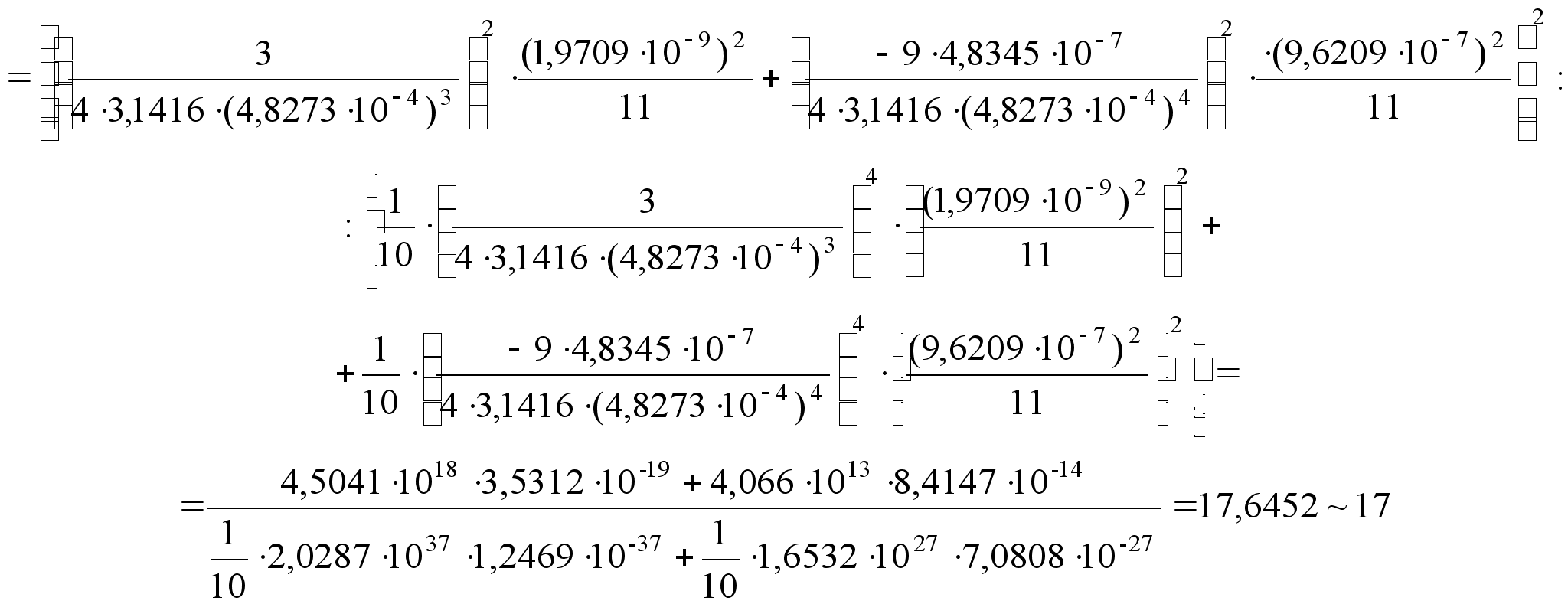
Определяем доверительный интервал для функции, для этого задаемся доверительной вероятностью P = 0,98 и из распределения Стьюдента находим t

n = m + 1 = 17 + 1 = 18

t = 2,57

(34)

Значение функции будет находиться в промежутке:

5. Определение погрешностей результатов измерений методом математической статистики

Условие. В ходе измерений физической величины получены 100 результатов измерения, представленных в таблице 11. Исключить погрешности и определить достоверный результат измерения.

Исходные данные:

Таблица 11

20,05	20,24	20,17	20,16	20,08	20,22	20,19
20,01	20,28	20,15	20,17	20,25	20,23	20,20
20,04	20,26	20,16	20,18	20,23	20,21	20,10
20,30	20,28	20,17	20,19	20,06	20,07	20,18
20,34	20,29	20,30	20,20	20,13	20,11	20,17
20,35	20,30	20,27	20,10	20,05	20,13	20,06
20,25	20,25	20,26	20,15	20,10	20,10	20,15
20,30	20,20	20,28	20,11	20,15	20,20	20,20
20,29	20,24	20,25	20,14	20,10	20,19	20,19
20,25	20,21	20,20	20,07	20,14	20,08	20,17
20,27	20,23	20,25	20,13	20,13	20,18
20,20	20,15	20,24	20,14	20,12	20,17
20,25	20,20	20,21	20,10	20,06	20,16
20,21	20,17	20,22	20,14	20,25	20,09
20,21	20,18	20,15	20,08	20,24	20,15

Расчет. Случайные погрешности, имеющие место при измерении, подчиняются закону нормального распределения, который графически изображается кривой Гаусса, имеющей симметричную форму с округленной вершиной и с каждой стороны по одной точке перегиба на некотором расстоянии от вершины.

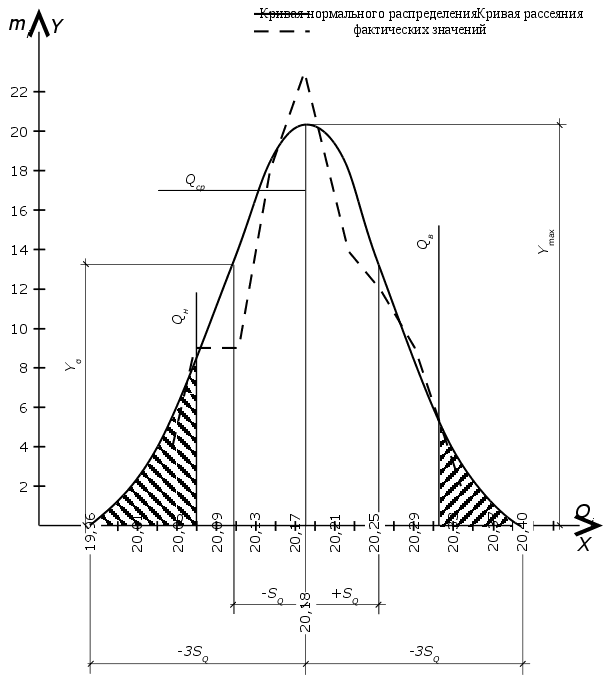
При проведении исследования, чтобы составить графики и определить, на сколько полученная кривая рассеяния фактических результатов измерения приближается к теоретической кривой нормального распределения, обе кривые надо начертить совмещёнными в одинаковом масштабе. С этой целью рассчитаем данные, необходимые для построения кривой нормального распределения. Для сокращения расчетов и упрощения примерного построения кривой нормального распределения можно ограничиться определением только трех параметров: максимальной ординаты Y_max (при X = 0), ординаты для точек перегиба Y_σ (при X = ±S_Q) и величины поля рассеяния.

Результаты измерения Q_i разбиваем на 9 групп через установленные интервалы с указанием абсолютной частоты (m_i) появления результата измерения внутри каждого интервала. Данные располагаем для удобства расчетов в форме таблицы (таблица 12), заполняемой по мере проведения расчетов.

Величина интервала определяется по формуле:

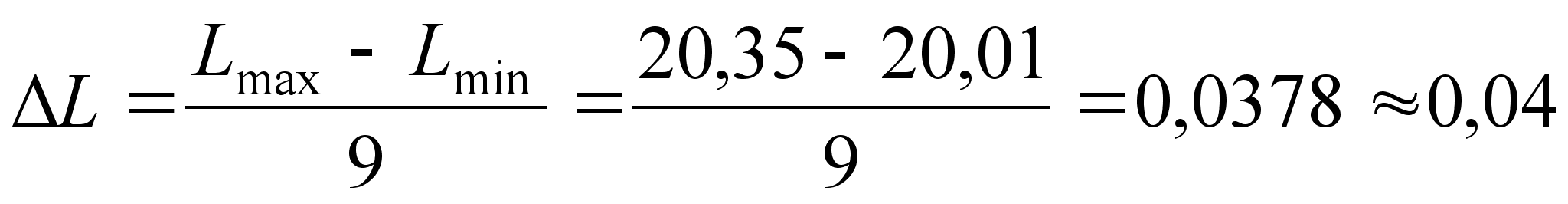(35)

Таблица 12

№ группы	Границы интервала	Qi	mi	Qi· mi
1	20,01-20,05	20,0375	4	80,15	-0,1470	21,5997	86,3989
2	20,06-20,09	20,0722	9	180,65	-0,1122	12,5992	113,3929
3	20,10-20,12	20,1044	9	180,94	-0,0800	6,4038	57,6345
4	20,13-20,16	20,1450	18	362,61	-0,0395	1,5578	28,0396
5	20,17-20,20	20,1857	23	464,27	0,0012	0,0014	0,0322
6	20,21-20,24	20,2243	14	283,14	0,0398	1,5854	22,1959
7	20,25-20,27	20,2550	12	243,06	0,0705	4,9747	59,6965
8	20,28-20,31	20,2911	9	182,62	0,1066	11,3727	102,3540
9	20,32-20,35	20,3450	2	40,69	0,1605	25,7704	51,5408
Σ			100	2018,13	0		521,2851

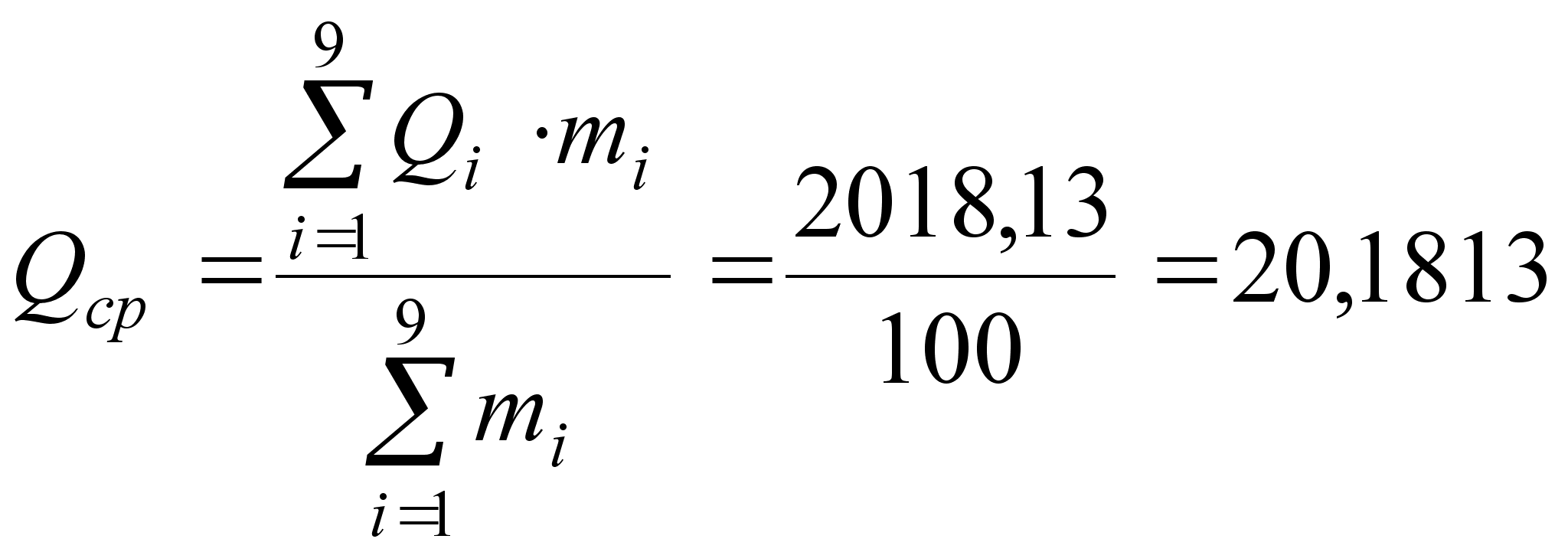(36)

Определим среднеквадратическое отклонение:

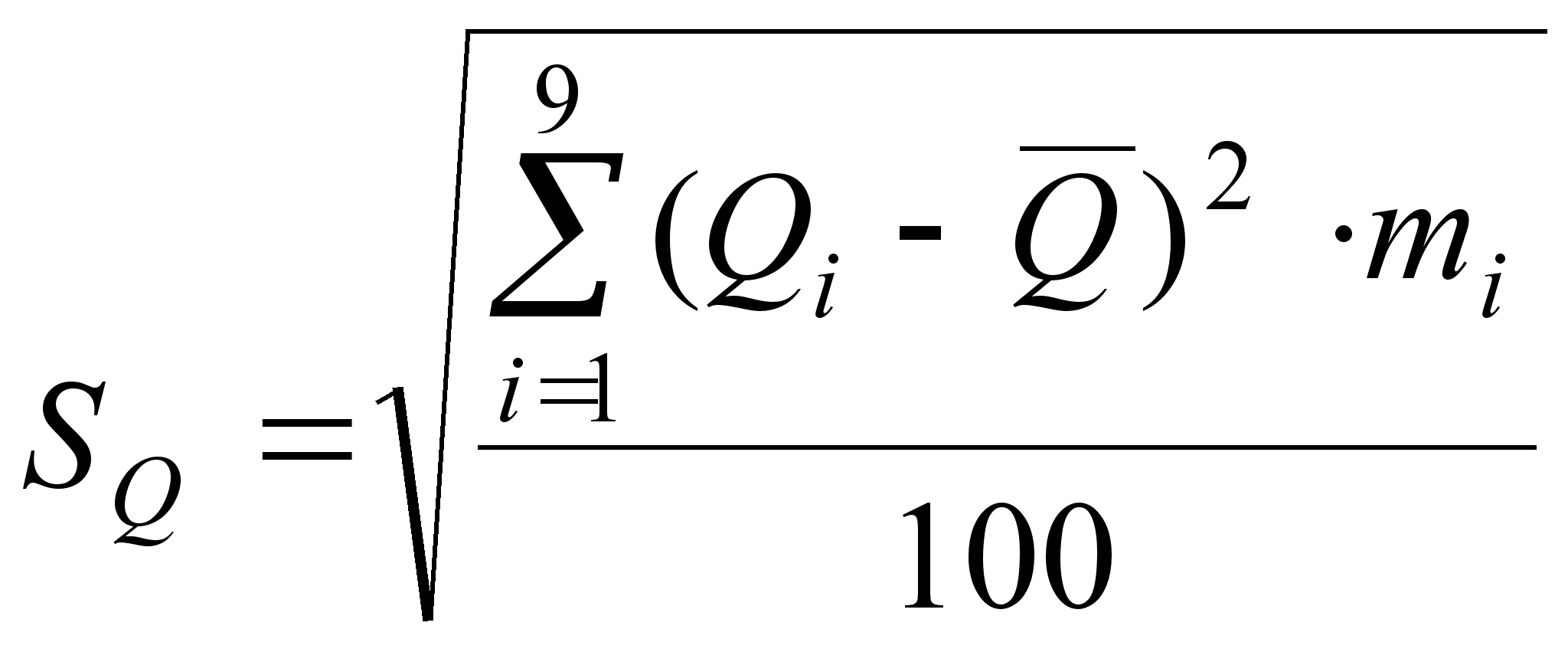(37)

Для построения кривой нормального рассеяния определим:

1. Y_max: 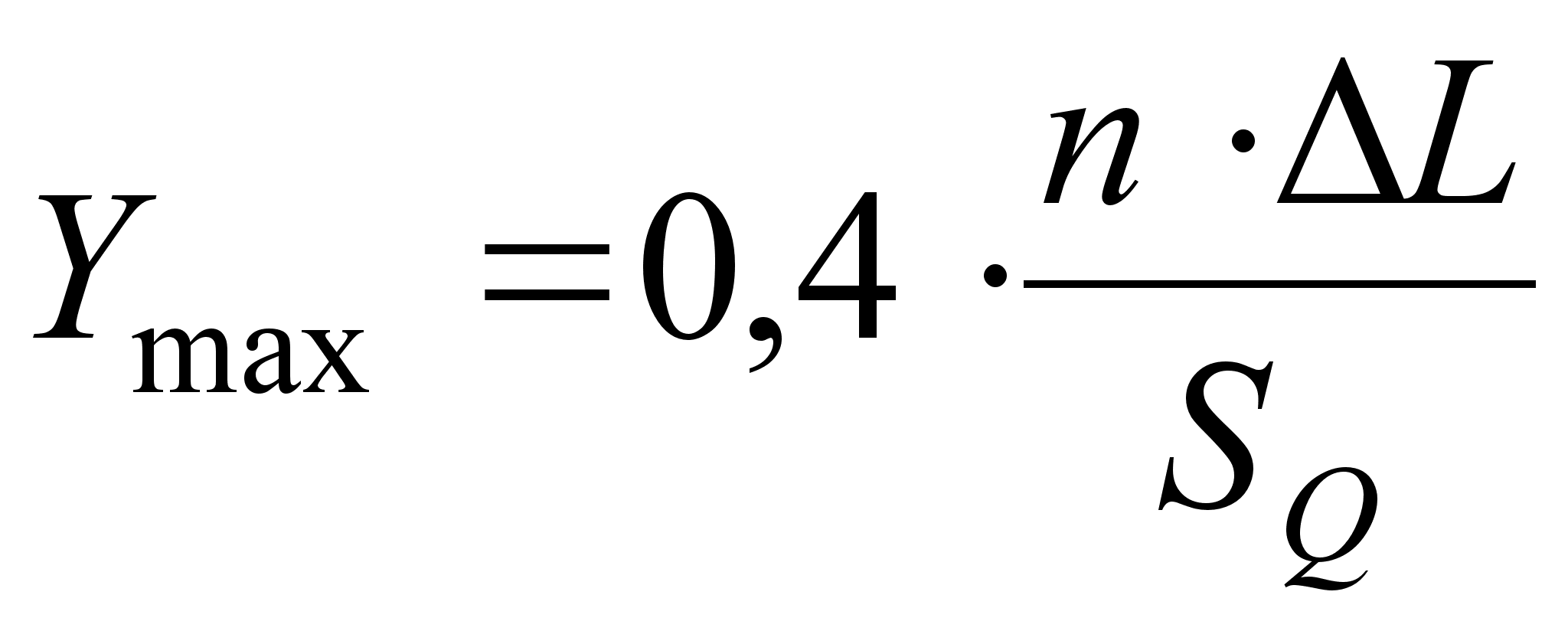(38)

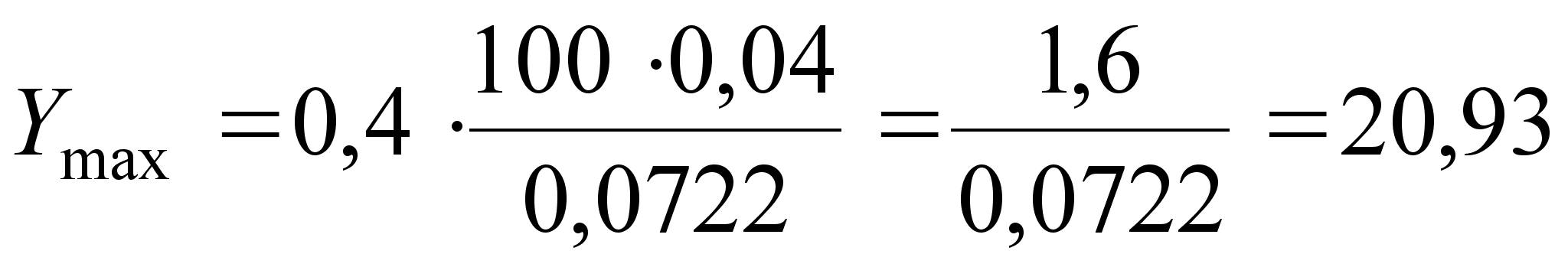
2. Y для точек перегиба (X = +σ):

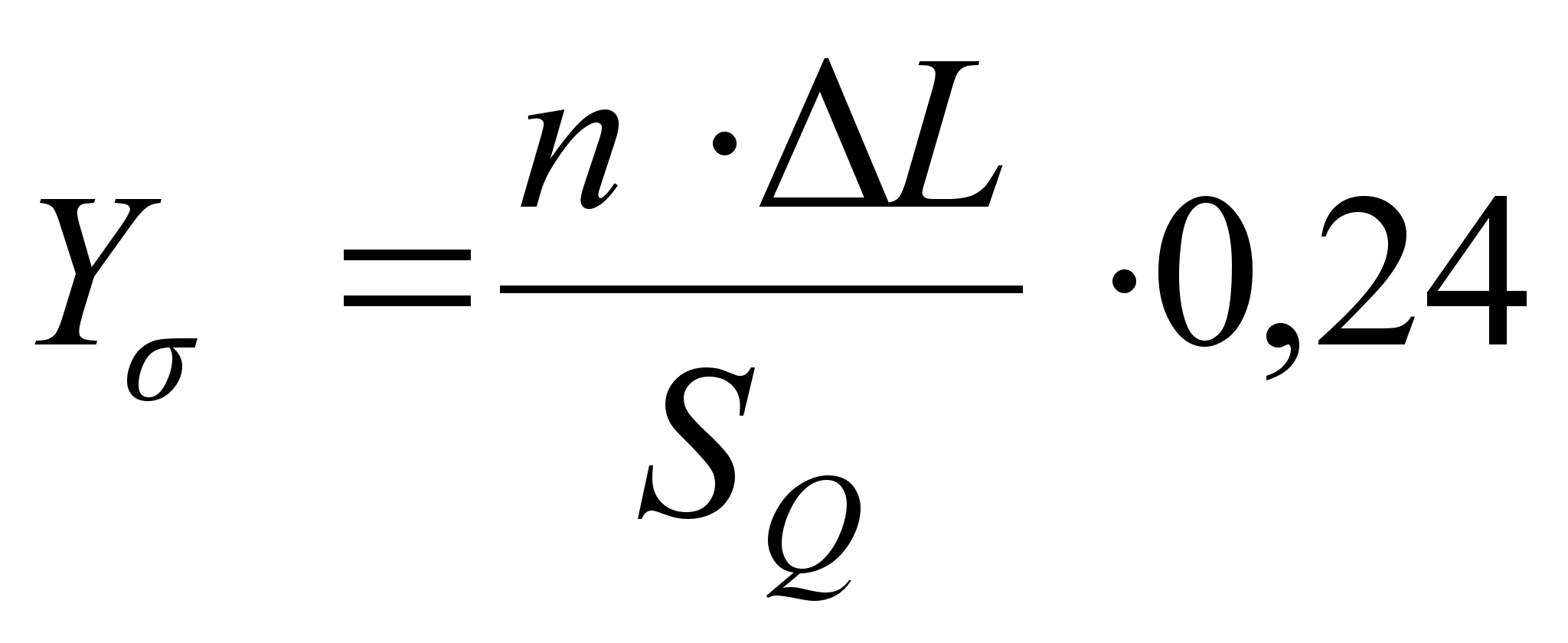(39)

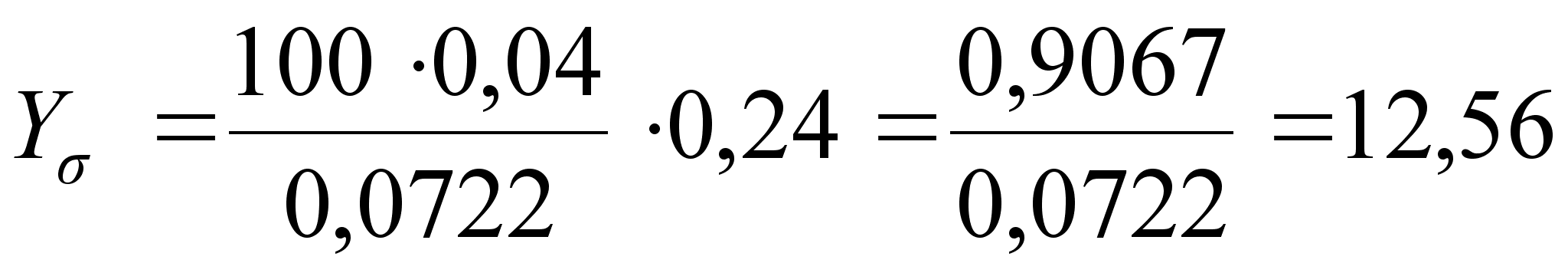
3. Величина поля рассеяния

4. Координаты кривой нормального рассеяния

По этим данным строится кривая нормального распределения непосредственно на графике рассеяния фактических значений.

Величина смещения центра поля рассеяния от середины области допустимых значений по абсциссе равна:

, (40)

где: Q_ср – абсцисса центра поля рассеяния;

Q_в – верхнее предельное значение области допустимых значений;

Q_н – нижнее предельное значение области допустимых значений.

Значения аргумента для верхнего и нижнего предельно допустимых значений определим по формулам:

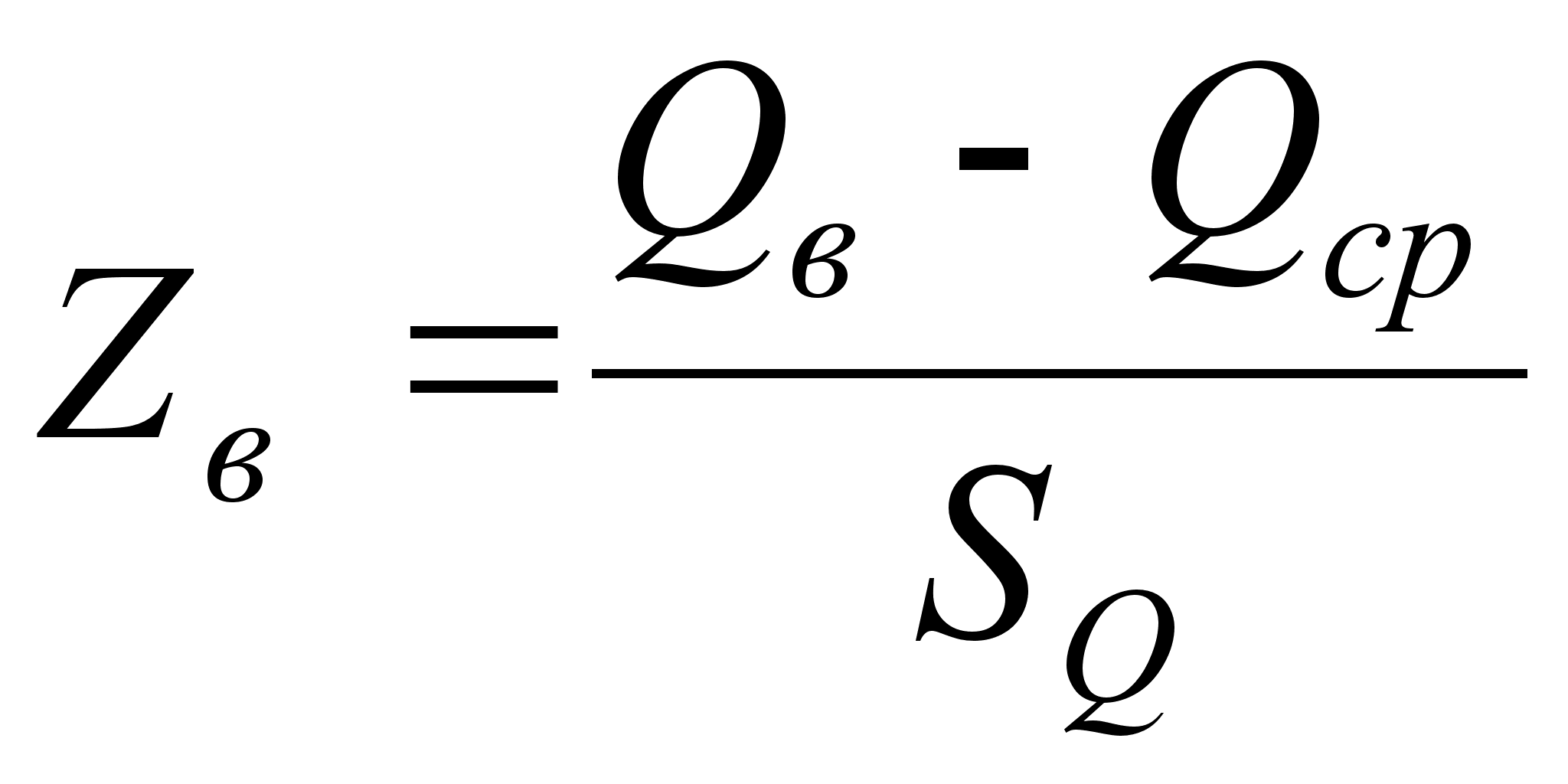, ; (41)

; ;

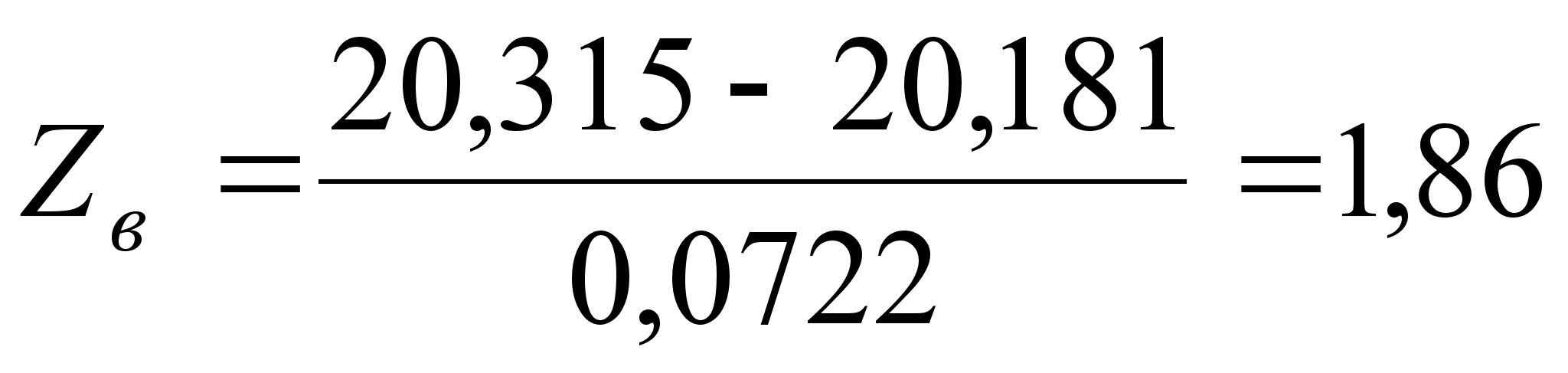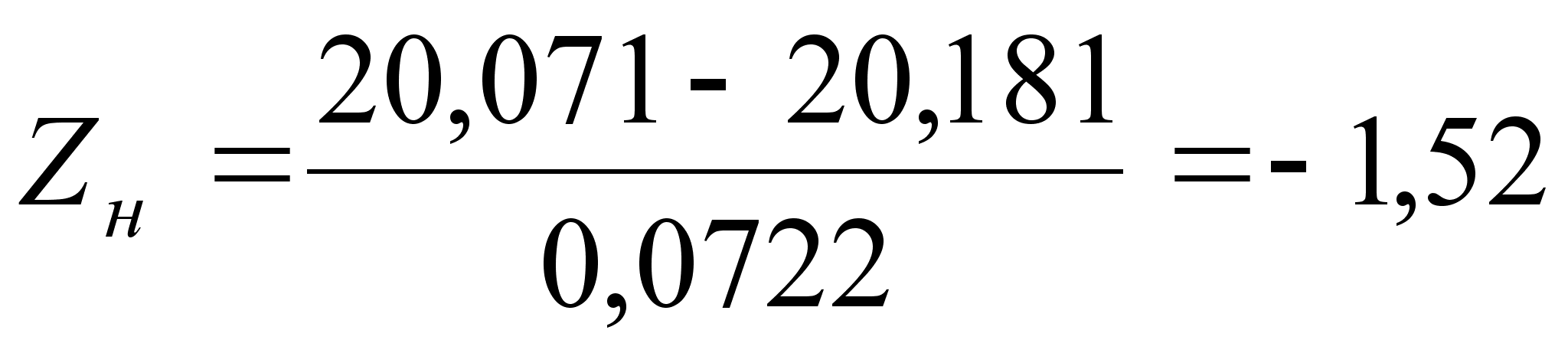Вероятность ошибки τ (%)

– по верхнему пределу, τ_в = [0,5–Ф(Z_в)]·100%=[0,5–Ф(1,86)]·100%=3,14%

– по нижнему пределу, τ_н = [0,5–Ф(Z_н)]·100%=[0,5–Ф(-1,52)]·100%=6,43%

Рис. 2. Кривая рассеяния фактических значений и

кривая нормального распределения

Литература

Шишкин И.Ф. Метрология, стандартизация и управление качеством – М.: Изд-во стандартов, 1990.

ГОСТ 8.401–80.

Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся вузов. – М.: Наука, 1986. – 544 с.

Атамалян Э.Г. Приборы и методы измерения электрических величин. – М.: Высшая школа, 1989. – 384 с.

1

30 Курсовая работа 30 30

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РФ

ОРЛОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Ливенский политехнический колледж

(филиал) Орел ГТУ

кафедра ПМиС

КУРСОВАЯ РАБОТА

по дисциплине: «Метрология, стандартизация и сертификация»

по теме: «Статистическая обработка экспериментальных данных»

Выполнил:

студент гр. 21 – с

направление 550100

курс 2

шифр 994145 ____________________Старина А.Г.

Работу проверил ____________________Бакурова Ю.А.

Оценка ___________________

Дата защиты ______________

ЛИВНЫ 200