Передаточные функции

2.6. Передаточные функции.

2.6.1 Определение передаточной функции.

Преобразование ДУ по Лапласу дает возможность ввести удобное понятие передаточной функции, характеризующей динамические свойства системы.

Например, операторное уравнение

3s²Y(s) + 4sY(s) + Y(s) = 2sX(s) + 4X(s)

можно преобразовать, вынеся X(s) и Y(s) за скобки и поделив друг на друга:

Y(s)*(3s² + 4s + 1) = X(s)*(2s + 4)

.

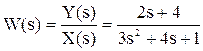Полученное выражение называется передаточной функцией.

Передаточной функцией называется отношение изображения выходного воздействия Y(s) к изображению входного X(s) при нулевых начальных условиях.

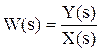(2.4)

Передаточная функция является дробно-рациональной функцией комплексной переменной:

,

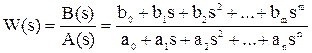где B(s) = b₀ + b₁s + b₂ s² + … + b_m s^m - полином числителя,

А(s) = a₀ + a₁s + a₂ s² + … + a_n sⁿ - полином знаменателя.

Передаточная функция имеет порядок, который определяется порядком полинома знаменателя (n).

Из (2.4) следует, что изображение выходного сигнала можно найти как

Y(s) = W(s)*X(s).

Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета АСР сводится к определению ее передаточной функции.

2.6.2 Примеры типовых звеньев.

Звеном системы называется ее элемент, обладающий определенными свойствами в динамическом отношении. Звенья систем регулирования могут иметь разную физическую основу (электрические, пневматические, механические и др. звенья), но относится к одной группе. Соотношение входных и выходных сигналов в звеньях одной группы описываются одинаковыми передаточными функциями.

Простейшие типовые звенья:

·     усилительное,

·     интегрирующее,

·     дифференцирующее,

·     апериодическое,

·     колебательное,

·     запаздывающее.

1) Усилительное звено.

Звено усиливает входной сигнал в К раз. Уравнение звена у = К*х, передаточная функция W(s) = К. Параметр К называется коэффициентом усиления.

Выходной сигнал такого звена в точности повторяет входной сигнал, усиленный в К раз (см. рис. 1.15).

Примерами таких звеньев являются: механические передачи, датчики, безынерционные усилители и др.

2) Интегрирующее.

2.1) Идеальное интегрирующее.

Выходная величина идеального интегрирующего звена пропорциональна интегралу входной величины.

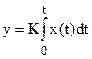; W(s) =

При подаче на вход звена воздействия выходной сигнал постоянно возрастает (см. рис. 1.16).

Это звено астатическое, т.е. не имеет установившегося режима.

2.2) Реальное интегрирующее.

Передаточная функция этого звена имеет вид:

W(s) = .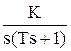

Переходная характеристика в отличие от идеального звена является кривой (см. рис. 1.17).

Примером интегрирующего звена является двигатель постоянного тока с независимым возбуждением, если в качестве входного воздействия принять напряжение питания статора, а выходного - угол поворота ротора.

3) Дифференцирующее.

3.1) Идеальное дифференцирующее.

Выходная величина пропорциональна производной по времени от входной:

; W(s) = K*s

При ступенчатом входном сигнале выходной сигнал представляет собой импульс (d-функцию).

3.2) Реальное дифференцирующее.

Идеальные дифференцирующие звенья физически не реализуемы. Большинство объектов, которые представляют собой дифференцирующие звенья, относятся к реальным дифференцирующим звеньям. Переходная характеристика и передаточная функция этого звена имеют вид:

W(s) = .

4) Апериодическое (инерционное).

Этому звену соответствуют ДУ и ПФ вида:

; W(s) = .

Определим характер изменения выходной величины этого звена при подаче на вход ступенчатого воздействия величины х₀.

Изображение ступенчатого воздействия: X(s) = . Тогда изображение выходной величины:

Y(s) = W(s) X(s) =  = K x₀.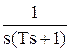

Разложим дробь на простые:

 =  +  =  =  -  =  -

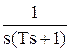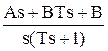Оригинал первой дроби по таблице: L^-1{} = 1, второй:

L^-1{} = .

Тогда окончательно получаем:

y(t) = K x₀ (1 - ).

Постоянная Т называется постоянной времени.

Большинство тепловых объектов являются апериодическими звеньями. Например, при подаче на вход электрической печи напряжения ее температура будет изменяться по аналогичному закону (см. рис. 1.19).

5) Колебательное звено имеет ДУ и ПФ вида

 ,

W(s) = .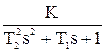

При подаче на вход ступенчатого воздействия амплитудой х₀ на переходная кривая будет

 иметь один из двух видов: апериодический (при Т₁ ³ 2Т₂) или колебательный (при Т₁ < 2Т₂).

6) Запаздывающее.

y(t) = x(t - t), W(s) = e^-ts.

Выходная величина у в точности повторяет входную величину х с некоторым запаздыванием t. Примеры: движение груза по конвейеру, движение жидкости по трубопроводу.

Похожие работы

Основы управления образовательными системами

Скачать

201630

6

6

... определенное время (период подготовки высококвалифицированного рабочего или специалиста). Взаимодействие государственных органов с заказчиками кадров призвано стимулировать гибкость и рационализацию управления образовательной системой, распределять между ними ответственность за процесс и качество профессиональной подготовки, сохраняя при этом единое образовательное пространство в государстве. ...

Управление образовательными системами

Скачать

115035

0

0

... на паритетных началах входят представители государственного органа управления образованием, соответствующего органа местного самоуправления и (или) местного (муниципального) органа управления образованием, действующих образовательных учреждений, общественности. Предметом и содержанием экспертизы является установление соответствия условий осуществления образовательного процесса, предлагаемых ...

Современное социальное управление - состояние, тенденции изменения

Скачать

60252

1

0

... потом и на развитие. В этом ей следует в большей мере опереться на свой исторический выбор, отклонения от которого всегда при­носили России беды и невзгоды. Глава 3. Тенденции изменения в социальном управлении Формирование гражданского общества на принципах корпора­тизма поставит под контроль государство, публичную власть, которые все в большей мере будут выполнять свою главную функцию, ...

Проектирование организационных структур государственного управления

Скачать

121657

0

5

... и характеристиками организационных структур. Они построены на основе сбора, анализа и обработки эмпирических данных об организациях, функционирующих в сопоставимых условиях. Процесс проектирования организационной структуры управления должен быть основан на совместном использовании охарактеризованных выше методов. 2.3 Тенденции проектирования структур управления Рассмотрение принципиальных ...