The Profit-Maximizing Firm

2.   The Profit-Maximizing Firm

Let us first examine some of the conventional theory of the profit-maximizing firm. In the chapter on the differential calculus, the basic marginal condition for profit maximization was derived as an illustration. Let us now rederive this marginal-cost-equals-marginal-revenue condition with the aid of a verbal and a geometric argument.

The proposition is that no firm can be earning maximum profits unless its marginal cost and its marginal revenue are (at least approximately) equal, i.e., unless an additional unit of output will bring in as much money as it costs to produce, so that its marginal profitability is zero.

It is easy to show why this must be so. Suppose a firm is producing 200,000 units of some item, x, and that at that output level, the marginal revenue from x production is $1.10 whereas its marginal cost is only 96 cents. Additional units of x will, therefore, each bring the firm some 14 cents = $1.10 — 0.96 more than they cost, and so the firm cannot be maximizing its profits by sticking to its 200,000 production level. Similarly, if the marginal cost of x exceeds its marginal revenue, the firm cannot be maxi­mizing its profits, for it is neglecting to take advantage of its opportunity to save money—by reducing its output it would reduce its income, but it would reduce its costs by an even greater amount.

C

We can also derive the marginal-cost-equals-marginal-revenue proposi­tion with the aid of Figure 1. At any output, OQ, total revenue is rep­resented by the area OQPR under the marginal revenue curve (see Rule 9 of Chapter 3). Similarly, total cost is represented by the area OQKC immediately below the marginal cost curve. Total profit, which is the dif­ference between total revenue and total cost is, therefore, represented by the difference between the two areas—that is, total profits are given by the lightly shaded area TKP minus the small, heavily shaded area, RTC. Now, it is clear that from point Q a move to the right will increase the size of the profit area TKP. In fact, only at output OQ_m will this area have reached its maximum size—profits will encompass the entire area TKMP.

 

 

 

 

 

 

 

 

	OUTPUT

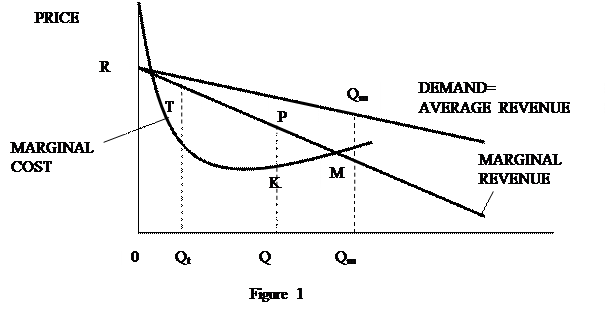
But at output OQ_m marginal cost equals marginal revenue—indeed, it is the crossing of the marginal cost and marginal revenue curves at that point which prevents further moves to the right (further output increases) from adding still more to the total profit area. Thus, we have once again estab­lished that at the point of maximum profits, marginal costs and marginal revenues must be equal.

Before leaving the discussion of this proposition, it is well to distinguish explicitly between it and its invalid converse. It is not generally true that any output level at which marginal cost and marginal revenue happen to be equal (i.e., where marginal profit is zero) will be a profit-maximizing level. There may be several levels of production at which marginal cost and marginal revenue are equal, and some of these output quantities may be far from advantageous for the firm. In Figure 1 this condition is satisfied at output OQ_t as well as at OQ_m. But at OQ_t the firm obtains only the net loss (negative profit) represented by heavily shaded area RTC. A move in either direction from point Q_t will help the firm either by reducing its costs more than it cuts its revenues (a move to the left) or by adding to its revenues more than to its costs. Output OQ_t is thus a point of minimum profits even though it meets the marginal profit-maximization condition, "marginal revenue equals marginal cost."

This peculiar result is explained by recalling that the condition, "mar­ginal profitability equals zero," implies only that neither a small increase nor a small decrease in quantity will add to profits. In other words, it means that we are at an output at which the total profit curve (not shown) is level—going neither uphill nor downhill. But while the top of a hill (the maximum profit output) is such a level spot, plateaus and valleys (minimum profit outputs) also have the same characteristic—they are level. That is, they are points of zero marginal profit, where marginal cost equals marginal revenue.

We conclude that while at a profit-maximizing output marginal cost must equal marginal revenue, the converse is not correct—it is not true that at an output at which marginal cost equals marginal revenue the firm can be sure of maximizing its profits.