Фирма, максимизирующая прибыль

2.   Фирма, максимизирующая прибыль.

Для начала исследуем некоторую имеющуюся теорию о фирме, максимизирующей прибыль. В главе, посвященной дифференциальным уравнениям, основное маржинальное условие для максимизации прибыли было показано на иллюстрации. Теперь рассмотрим это условие («предельные издержки равняются предельному доходу») с помощью словесного и геометрического аргументов.

Предположение, что фирма не может заработать максимальную прибыль, если её предельные расходы не равны предельному доходу (или, по крайней мере, близки), т.е. если дополнительная единица выпуска не принесёт столько же дохода, сколько израсходовано при производстве, таким образом, предельная прибыльность равна нулю.

Легко показать, почему так должно быть. Предположим, что фирма, производящая 200000 единиц некоторого продукта x и при таком уровне производства предельный доход составит 1.1 $, тогда как её маржинальные издержки составят только 96 центов. Каждая дополнительная единица x принесет фирме 14 центов (= 1,10-0,96); это больше, чем фирма израсходовала, и таким образом, фирма не может максимизировать свои прибыли, пренебрегая возможностью сохранить деньги – снижая свой объем производства, это снизит его доход, но это же снизит расходы, даже в большем объеме.

Также предположение, что «предельные издержки равняются предельному доходу», можно показать с помощью рисунка 1.

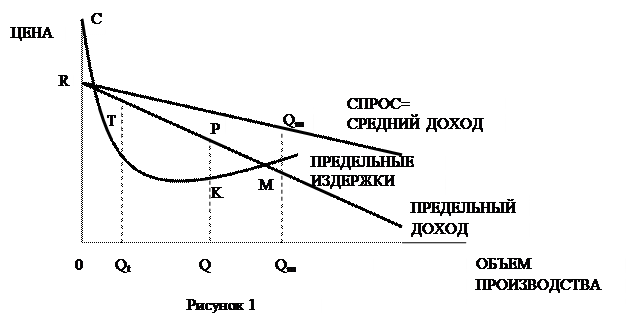
При любом выпуске OQ совокупный доход представлен площадью OQPR под кривой предельного дохода. Подобно этому, общие расходы представлены площадью OQKC под кривой предельных издержек. Общая прибыль, которая есть разница между общим доходом и общими издержками, таким образом представлена разницей между двумя площадями – общая прибыль показана светло закрашенной площадью TKP минус небольшая, сильно закрашенная площадь RTC. Теперь ясно, что из точки Q движением вправо увеличивается размер площади прибыли TKP. В действительности, только при выпуске _m эта площадь достигнет своего максимального размера – прибыль будет занимать площадь TKMP. Но при выпуске _m  предельные издержки равны предельному доходу – на самом деле это пересечение в этой точке кривых предельных издержек и предельного дохода, которое предотвращается дальнейшим движением вправо (дальнейшее увеличение производства) при ещё большем увеличении площади совокупных прибылей. Таким образом, предельные издержки должны равняться предельному доходу.

Прежде чем оставить обсуждение этого предположения, хорошо было бы точно различить его и его толкование. Не совсем верно, что любой уровень объема производства, при котором предельные издержки равны предельному доходу (т.е. прибыль равна нулю) будет уровнем максимизации прибыли. Могут быть уровни производства продукции, при которых предельные издержки равны предельному доходу, и некоторые из них могут быть далеки от выгодных для фирмы. На рисунке 1 это условие подтверждается при выпуске OQ_t также, как и при выпуске _m. Но при выпуске OQ_tфирма получает только чистые убытки (отрицательную прибыль), представленную сильно закрашенной площадью RTC. Движения в любом направлении от точки Q помогут фирме либо снижением издержек большим, чем уменьшением доходов (перемещения влево), либо повышением доходов большим, чем издержек. Объем производства OQ_t таким образом является точкой минимума прибыли, даже если он удовлетворяет условию максимизации прибыли – «предельные издержки равняются предельному доходу».

Этот необычный результат объясняется отменой условия, что предельная прибыльность равна нулю, означающего только то, что ни малое увеличение, ни малое уменьшение объема производства не увеличит прибыли. Другими словами, это означает, что мы при объеме производства, при котором кривая общей прибыли (на рисунке не показана) есть прямая, не двигаемся ни вверх, ни вниз. Но до тех пор, пока вершина кривой (объем производства максимальной прибыли) есть точка уровня, «плато и долины» (объем производства минимальной прибыли) также имеют характеристики – они будут прямыми. Это есть точки нулевой предельной прибыли, где предельные издержки равны предельному доходу.

Делаем заключение, что вывод о том, что при объеме производства, максимизирующего прибыль, предельные издержки равны предельному доходу, неверен – неверно то, что при выпуске, при котором предельные издержки равны предельному доходу, фирма будет точно максимизировать прибыль.

3.   Приложение: Ценообразование и изменение издержек

Предыдущая теорема позволяет нам сделать предположения о поведении фирмы, максимизирующей прибыль, и установить некоторые нормативные правила исследования операций для её действий. Мы можем определить не только оптимальный объем производства, но также цену максимизации прибыли с помощью кривой спроса для произвольного продукта фирмы. Для данного оптимального выпуска мы можем определить по кривой спроса, какая цена позволит компании продать выпущенное количество продукции. На рисунке 1, где оптимальный объем производства есть _m, мы видим, что ему соответствует цена Q_mP_m, где точка P_mявляется точкой на кривой спроса, соответствующей точке Q_m(точка P_mне является точкой пересечения кривых предельных издержек и предельного дохода).

 В предыдущем разделе главы было показано, как наша теорема может также предсказать эффект изменения налоговых ставок или некоторых других изменений в расходах фирмы или ценообразовании. Мы можем просто определить, как перемещения по кривой предельных издержек определят новую комбинацию значений цены-выпуска, максимизирующих прибыль, путем определения новой точки пересечения кривых предельных издержек и дохода. Отменим полученный особый результат для использования его позже в этой главе – теоремы об эффектах при изменении постоянных издержек. Напомним, что изменение постоянных издержек никогда не ведет к изменению кривой предельных издержек фирмы, потому что предельные постоянные издержки всегда равны нулю (по определению, что дополнительная единица производства не увеличивает постоянные издержки). Отсюда следует, если арендная плата фирмы, максимизирующей прибыль, её налоги или некоторые другие постоянные издержки увеличиваются, тогда не будет изменений значений цены-выпуска, при которых предельные издержки и предельный доход равны. Другими словами, фирма, максимизирующая прибыль, не изменит цены и выпуска, чтобы соответствовать некоторым увеличению или уменьшению в их постоянных издержках! Этот довольно неожиданный результат не соответствует обычной деловой практике и требует некоторого дальнейшего пояснения, которое будет сейчас представлено.