Навигация
Если последовательность Хn монотонна и ограничена, то она имеет предел (сходится)
7 Если последовательность Хn монотонна и ограничена, то она имеет предел (сходится).
Cвойства пределов:
если Хn=С то lim Xn=C
n→∞
пусть lim Xn=A, a lim Yn=B тогда lim (Xn±Yn)=A±B
n→∞ n→∞ lim (Xn*Yn)=A*B
lim (Xn/Yn)=A/B ; B≠0
если Xn≤Yn для n∈N то lim Xn ≤ lim Yn
n→∞ n→∞
8 Eсли Хn сходится (имеет предел) то Хn ограничена
Последовательность Xn; n∈N наз. ограниченной если существует положительное число М, что выполняется нер-во | Xn |≤M; n∈N
Если lim Xn=0, то Xn; n∈N наз. БМВ обознач (αn,βn,γn)
n→∞
Св-ва БМВ:
lim αn=0
n→∞
lim (αn±βn)=0
n→∞
lim (Xn*αn)=0; если Xn-ограничена
n→∞
В произведении БМВ можно заменять на эквивалентную БМ. В алгебраической сумме замену можно производить в том случае если не происходит сокращения БМ одного порядка с Х:
sin X ~ X eЄ-1 ~ a
tg X ~ X (1+x)Є ~ ax
1 – cos X ~ XІ/2 arctg X ~ X
LOGe(1+X) ~ X xЄ-1 ~ aLNx
9 Сумма эл-тов числовой последовательности наз. числовым рядом.
![]()
Сумма n членов ряда – n частичная сумма ряда
Если при n→∞ lim Sn=S, то ряд сходящийся, S сумма ряда .
Ряд наз. сходящимся если сущ. конечный предел последовательности его частичных сумм.
Прим:
![]() при
каких q
сходится
и расходится
?
при
каких q
сходится
и расходится
?
сходится к сумме S=a/1-q при | q |0
Признак Лейбница:
Если члены ряда (знакопер) убывают а1>a2>a3>…An и
предел Аn при n→∞ =0 то ряд сходится
пример 1-1/2+1/3-1/4…+(-1)(n-1)*1/n
13 Имеет место функциональная зависимость между двумя переменными величинами х и у если задан закон y=f(x), согласно которому каждому х∈Х соответствует значение y∈Y. х-аргумент
y=kx+b – линейная ф-ия
y=axІ+bx+c – квадратичная ф-ия
Обратная ф-ия – ф-ия x=φ(y) наз. обратной ф-ией к прямой ф-ии y=f(x) если x=φ(f(x)) для всех х∈Х
Графики взаимно обратных ф-ий симметричны относительно прямой у=х.
y=XЄ и y=LOGxA – примеры
14 Число B называется пределом ф-ии в f(x) при x, стремящемуся к x0 (или в точке x0) если для любого, сколь угодно малого положительного числа ε>0, найдётся такое положительное число δ(ε)>0 что для всех х не равных х0 и удовлетворяющих условию | x-x0 |=0 и –x при x=0 из определения(|x|=max{x, -x})
2)-|x|, существует предел limy0x/y=1/(limy0y/x)=1/f'(x). Этим формула [1] доказана. Примечание: Если f'(x)0 непрерывна на (a,b), то g'(y) непрерывна на (A,B). Это следует из [1], где можно положить x=g(y): g'(y)=1/f'[g(y)] (y(A,B)). Ведь сложная функция f'[g(y)], состоящая из непрерывных функций f' и g, непрерывна.
Основные
формулы: 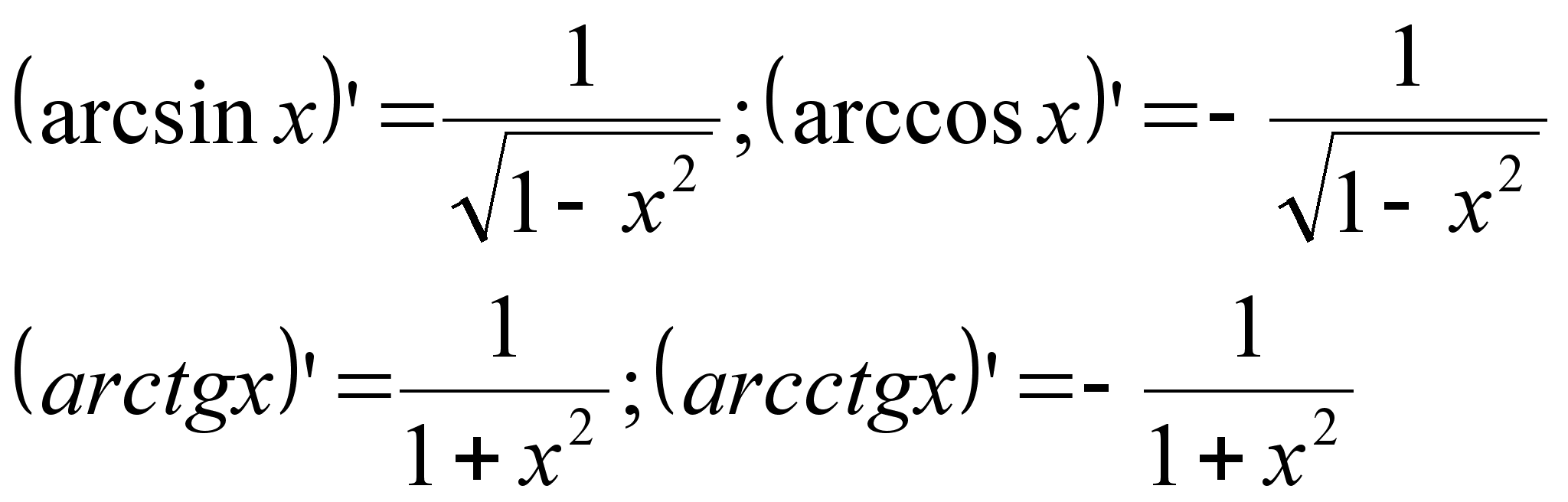
Для сложных функций:
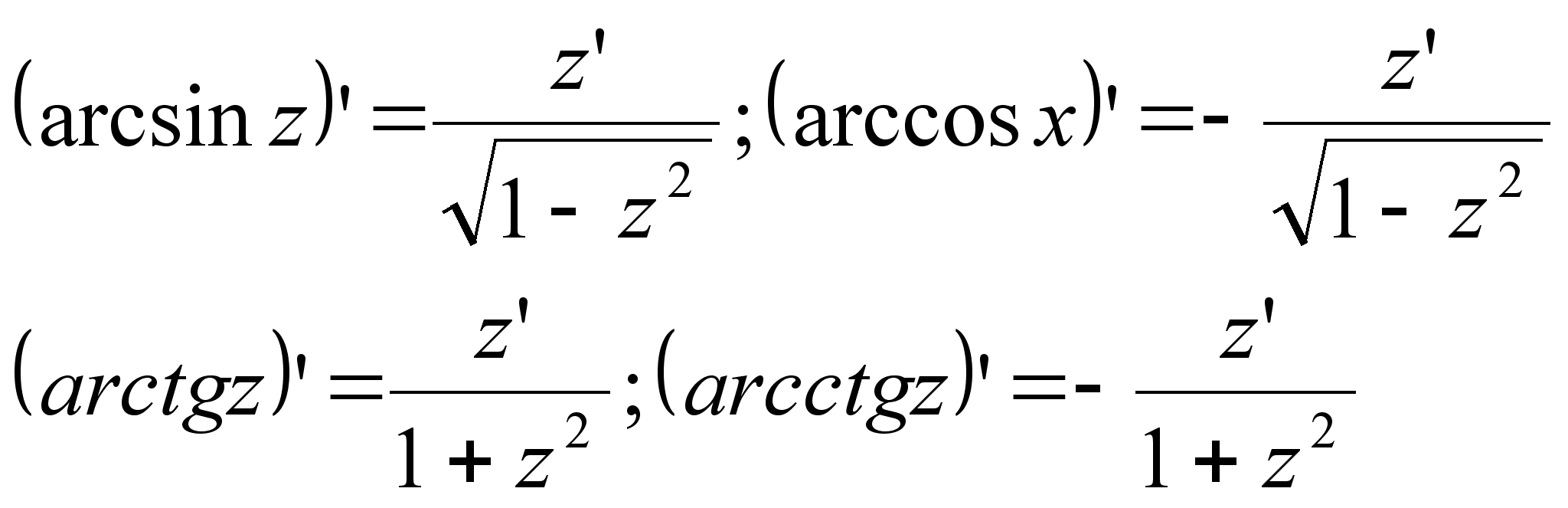
В20.Производная сложной функции. Логарифмическая производная. Производная функции,заданной неявно.
Теорема №1: Если функция x=(t) имеет производную в точке t, а функция y=f(x) имеет производную в точке х, то сложная функция у=F(t)=f[(t)] (1) имеет производную (по t) в точке t и справедлива равенство F'(t)=f'(x)'(t) (2) или y't=y'xx't (3) Доказательство: Зададим t, ему соответствует значение х=(t). Придадим t приращение t0. это вызовет приращение x=(t+t)– (t). Так как функция y=f(x) имеет производную в точке х, то на основании равенства f'(x)=lim(x0)y/x=lim(x0)f(x+x)–f(x)/x, имеем
y=f'(x)x+(x)x (4), где (x)0 при х0. Будем считать, что (0)=0. Равенство (4) при этом соглашении выполняется, т.к. если подставить в него x=0, то получится 0=0. Разделим теперь равенство (4) на t0: y/t=f'(x)(x/t)+ (x)(x/t) (5). Пусть t0. Тогда, потому что функция x(t)(t) имеет производную в точке t и, =>, непрерывна. Переходим в равенстве (5) к пределу при t0. Тогда x0 и (x)0, поэтому получим y't=f'(x)x'(t)+0x'(t)=f'(x)x'(t)=y'xx't. Теорема доказана.
Формула (1) может быть усложнена. Например, если – z=f(y), y=(x), x=() и все три функции имеют производные в соответствующих точках, то z'=z'yy'xx'
Логарифмическое дифференцирование
Если требуется
найти ![]() из
уравнения
из
уравнения ![]()
![]() ,
то можно:
,
то можно:
а) логарифмировать
обе части уравнения
![]() ;
;
б) дифференцировать
обе части полученного
равенства, где
![]() есть
сложная функция
от х,
есть
сложная функция
от х, 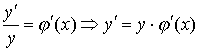 .
.
в) заменить
![]() его
выражением
через х
его
выражением
через х ![]() .
.
Пример: ![]()

§6.
Метод логарифмического
дифференцирования. 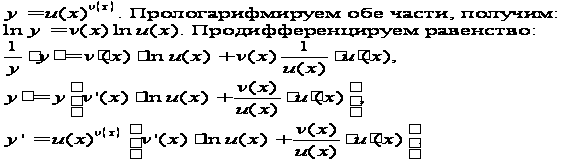
5. Дифференцирование неявных функций Пусть уравнение
Пример:![]() .
.
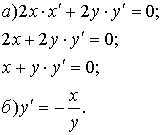
В21.Приращение и дифференциал функции одной переменной.Условия существования диффренциала. Инвариантность форм записи дифференциала первого порядка.
Дифференциал функции:
Пусть функция y=f(x) дифференцируема в точке х: т.е. для её приращения у в этой точке выполняется равенство [2]. Тогда у есть сумма двух слагаемых. Первое из них A x пропорционально x, а в таких случаях говорят, что оно есть линейная однородная функция от х. Второе – о(х)x0 является бесконечно малой функцией высшего порядка малости сравнительно с x. Если А0, то второе слагаемое стремится к нулю при x0 быстрее, чем первое. В связи с этим первое слагаемое A x=f'(x)x наз. главным членом приращения y. Это слагаемое называют дифференциалом функции и обозначают символом dy. Итак, по определению dy=df=f'(x)x. На (рис. 47) изображен график Г функции y=f(x);
Т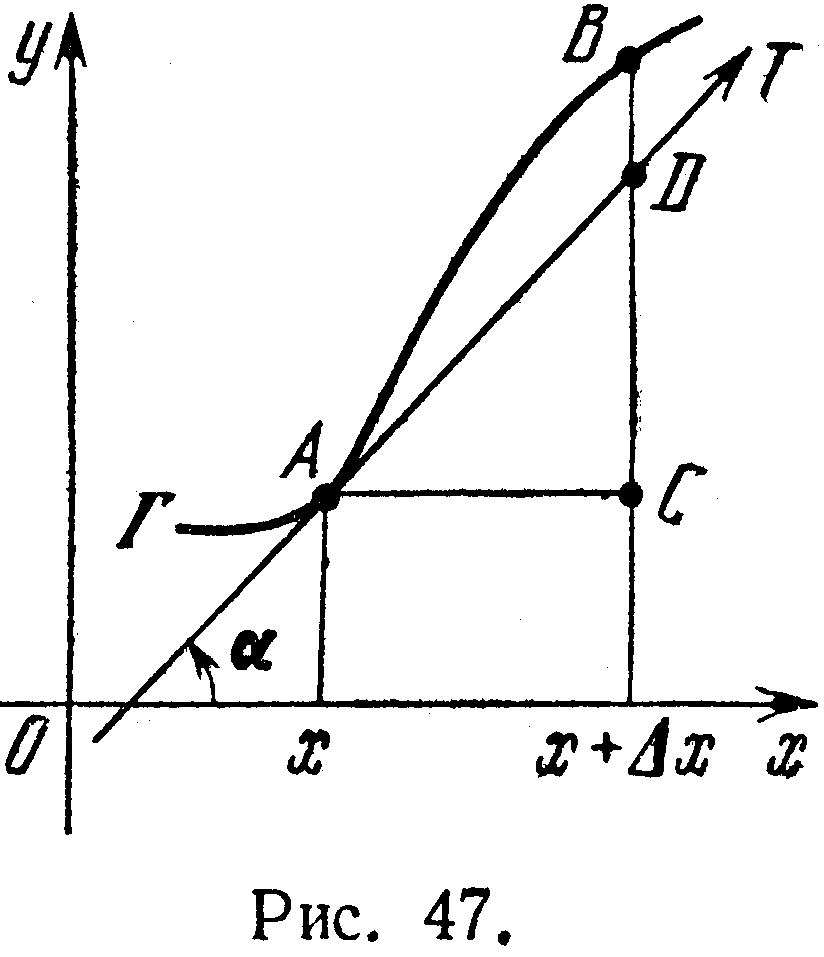 –касательная
к Г в точке A,
имеющей абсциссу
х; f'(x)=tg,
где
– угол, образованный
касательной
с осью х; dy=f'(х)x=tgx=CD,
DB=y–dy=o(x)x0.
Таким образом,
дифференциал
функции у в
точке х, соответствующий
приращению
x,
есть приращение
ординаты точки,
лежащей на
касательной
(dy=CD).
Вообще
говоря, dyy,
ибо y=dy+
o(x)x0,
а второй член
этой суммы,
вообще говоря,
не равен нулю.
Только для
линейной функции
у=Ах+В имеет
место равенство
у=А
x=dy
для любого х.
В частности,
для у=х, dy=dx=x
т.е. дифференциал
и приращение
независимой
переменной
равны между
собой (dx=x).
Поэтому
дифференциал
произвольной
функции f обычно
записывают
так: dy=f'(x)dx,
откуда f'(x)=dy/dx,
–касательная
к Г в точке A,
имеющей абсциссу
х; f'(x)=tg,
где
– угол, образованный
касательной
с осью х; dy=f'(х)x=tgx=CD,
DB=y–dy=o(x)x0.
Таким образом,
дифференциал
функции у в
точке х, соответствующий
приращению
x,
есть приращение
ординаты точки,
лежащей на
касательной
(dy=CD).
Вообще
говоря, dyy,
ибо y=dy+
o(x)x0,
а второй член
этой суммы,
вообще говоря,
не равен нулю.
Только для
линейной функции
у=Ах+В имеет
место равенство
у=А
x=dy
для любого х.
В частности,
для у=х, dy=dx=x
т.е. дифференциал
и приращение
независимой
переменной
равны между
собой (dx=x).
Поэтому
дифференциал
произвольной
функции f обычно
записывают
так: dy=f'(x)dx,
откуда f'(x)=dy/dx,
т.е. производная функции f в точке х равна отношению дифференциала функции в этой точке к дифференциалу независимой переменной х.
Это объясняет, что выражение dy/dx употребляется как символ для обозначения производной. Надо иметь в виду, что дифференциал dx независимой переменной не зависит от х, он равен x – произвольному приращению аргумента х. Что же касается дифференциала dy функции у (отличной от х), то он зависит от х и dx. Отметим формулы:
d(u)=dud [3]; d(u)=ud+du [4]; d(cu)=cdu (c – постоянная) [5]; d(u/)=(du–ud)/2 (при 0) [6]; где предполагается, что u и – дифференцируемые функции в рассматриваемой точке х. Например, формула [6] доказывается так:
![]()
Определение: Пусть y=f(x) определена в некоторой О(х0) – она называется дифференцируемой в точке х0, если её приращение в этой точки представимо в виде:
∆y=∆f(x0)=A∆x+(∆x)∆x)1
(0)=0 A=const
Определение: линейная ∆х часть приращение дифференцируемой функции называется дифференциалом функции в точке х0:
dy=df(x0)A∆x
Теорема: Если функция дифференцируема в точке х0 то A=f’(x0), то она имеет производную в этой точке, то A=f’(x0); наоборот если функция имеет производную в этой точке, то она дифференцируема в этой точке – называется дифференциалом.
Доказательство: Пусть y=f(x) дифференцируема в точке х0, то есть в некоторой О(х0) справедливо равенство ∆f(x0)=A∆x+(∆x)∆x1; (0)=0. Поделим обе части этого равенства на ∆х и приведём к пределу при ∆х0:
lim(∆f(x0))/∆x=lim(A+(x))=A. Этот предел существует, меньше , тогда по определению этот предел есть
∆x
0 комментариев