∆

производная.

Доказательство: (в обратную сторону) Пусть в точке х₀  f’(x₀)( dy=f’(u)g’(x)dx но g’(x)dx=du поэтому dy=f’(u)du

В22.Геометрический смысл дифференциала функции одной перменной. Касательная и нормаль к плоскости.

Геометрический смысл дифференциала функции и уравнение касательной.

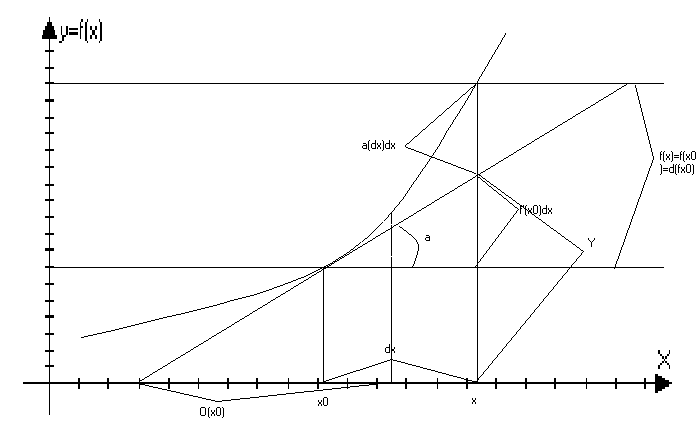
f’(x₀)=tg

уравнение прямой : Y=kx+b

y₀=f(x₀)=kx₀+b

k-угловой коэффициент прямой

k=tg=f’(x₀)

Y=f(x₀)+f(x₀)-f’(x₀)x₀

b=f(x₀)-kx₀

Y=f(x)+f’(x₀)(x-x₀)

∆f(x₀)=f’(x₀)∆x+(∆x)∆x при ∆х0  в некоторой

O(x₀) f(x₀)=f’(x₀)+f’(x₀)∆x+(∆x)∆x при ∆х0

Y¹=f(x₀)+f’(x₀)(x-x₀)^a=f’(x₀)+f’(x₀)∆x

df(x₀)=f’(x₀)∆x

Геометрический смысл дифференциала:

df(x₀) – это приращение ординаты при движение по касательной проведённой к графику функции в точки (х₀;f(x₀).

Замечание: Часто говорят о касательной проведённой в точке х₀.

Линеаризация функции.

Определение: Замена функции в окрестности данной точки линейной функции называется линеаризацией функции, точнее в О(х₀) заменяется отрезком касательной в точке х₀.

(*) f(x)-Y=(∆x)∆x-o(∆x)

Если в равенстве (*) отбросить правую часть, то мы

получим приближённое равенство:

f(x)f(x₀)+f’(x₀)(x-x₀), xx₀

Y=f(x₀)+f’(x₀)(x-x₀) – уравнение касательной в точке х₀

Формула получена из определения дифференциала в точке х₀ функции

f(x)=f(x₀)+f(x₀)∆x+o∆x при ∆х0 – называется критерием дифференциальности функции в точке х₀.

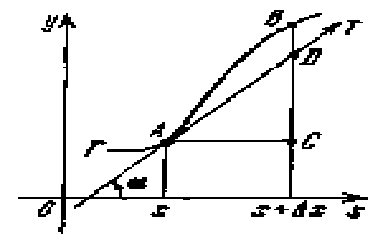
Рассмотрим кривую, уравнение которой есть y=f(x). Возьмем на этой кривой точку М(х, у), и составим уравнение касательной к данной кривой в точке М, предполагая, что эта касательная не параллельна оси Оу.

Уравнение прямой с угловым коэффициентом в общем виде есть у=kх + b. Поскольку для касательной k=f ў(x), то получаем уравнение y=f ў(x)Чx + b. Параметр b найдем из условия, что касательная проходит через точку М(х,). Поэтому ее координаты должны удовлетворять уравнению касательной: у= f ў(x)Чx + b . Отсюда b=y– f ў(x)Чx.

Таким образом, получаем уравнение касательной y=f ў(x)Чx +y - f ў(x)Чx или

Если касательная, проходящая через точку М(х,) параллельна оси ординат (т.е. производная в этой точке не существует), то ее уравнение х=х.

Н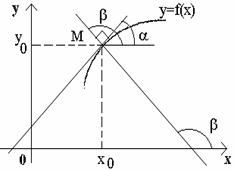аряду с касательной к кривой в данной точке часто приходится рассматривать нормаль.

Нормалью к кривой в данной точке называется прямая, проходящая через эту точку перпендикулярно к касательной в данной точке.

Из определения нормали следует, что ее угловой коэффициент связан с угловым коэффициентом касательной к равенством:

= tg b = tg(90° + a) = - ctg a =  = =.

Учитывая, что нормаль также как и касательная проходит через точку М(х, у), то уравнение нормали к кривой y=f(x) в данной точке М имеет вид:

Ясно, что если касательная параллельна оси Ох, т.е. f ў(x)=0 и ее уравнение имеет вид у=у, то нормаль в этой же точке будет перпендикулярна оси Ох. Значит, ее уравнение имеет вид х=х.

В23.Производные и дифференциалы порядка выше первого функции одной переменной. Нарушение инвариантности форм записи. Линейная замена переменной. Производные функции, заданной параметрически.

Существует f’(x)  x(a,b), тогда эта производная сама является функцией х (х)=f’(x) и можно ставить о дифференцируемости этой функции.

Существует ’(x)  x(a,b), то мы называем её второй производной ’(x)f’’(x)

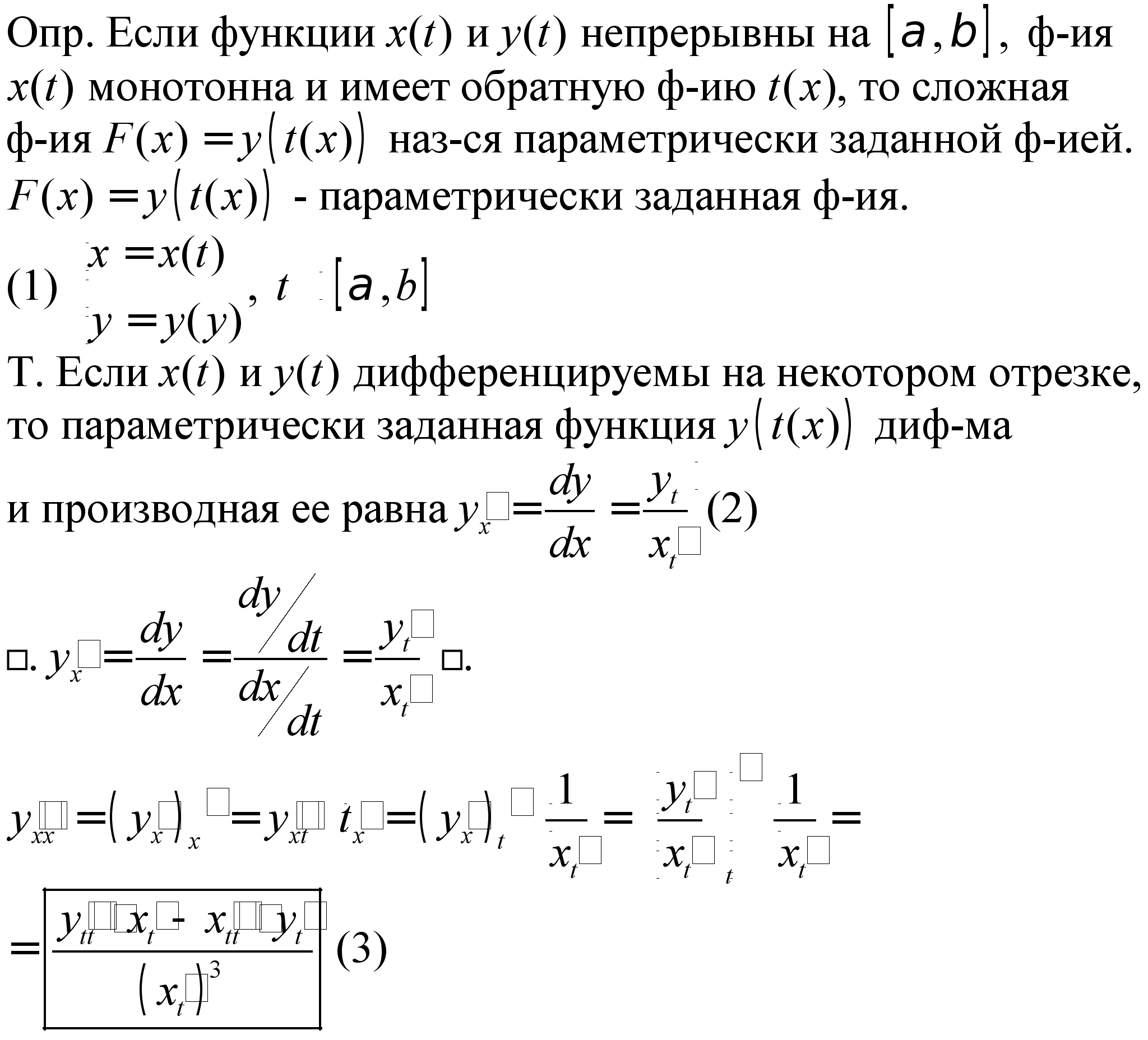
Диф.высших порядков не инвариантен: d² y=d(F’(u)du) Но здесь du=g’(x)dx зависит от х и поетому мы получаем d²y=d(F(u))du+F’(u)d(du) или d²y=F’’(u)(du)²+F’(u)d²u где d²u=g’’(x)(dx)²

Дифференцирование функций, заданных параметрически

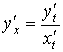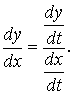Пусть функция задана параметрическими уравнениями ,тогда , или риме: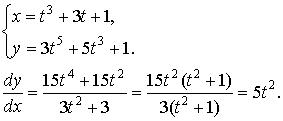

В24.Точка монотонности функции и достаточное условие их существования.Точки экстремума функции.Необходимое условие экстремума функции..

Если x₂>x₁, f(x₂)>f(x₁), то ф-ция монотонно возрастает

Если x₂>x₁, f(x₂)=0)

2)если ф-ция f(x) всюду в интервале убывает, то ее производная в этом интервале неположительная (f`(x)f(x₁)

2. если f`(a)0

если tg0, то функция z=f(х,у) имеет в точке Р₀(x₀,y₀) экстремум, а именно – максимум при А0); [2] если D