Вычисление определенного интеграла методом “Монте-Карло”
b
Определенный интеграл I = ò f(x)dx по методу “Монте-Карло”
n a
по формуле I = (1/n)* å (f(xi))/(g(xi)) ,где n – число испытаний ;g(x) – плотность
i=1 b
распределения “вспомогательной” случайной величины X, причем ò g(x)dx = 1 ,
a
В программе g(x) = 1/(b-a) .
Программа написана на языке TURBO PASCAL 7.0
Program pmk;
Uses crt;
Var k,p,s,g,x,Integral : real;
n,i,a,b : integer;
BEGIN
randomize;
writeln(‘Введите промежуток интегрирования (a;b):’);
readln(a);
readln(b);
writeln(‘Введите количество случайных значений(число испытаний):’);
readln(n);
k:=b-a;{Переменной“k”присвоим значение длины промежутка интегрирования}
writeln(‘k=’,k);
for i:= 1 to n do begin {проведем n испытаний}
g:=random; {g – переменная вещественного типа,случайная величина из
промежутка [0;1]}
x:= a + g*(b-a);{По этой формуле получается произвольная величина из [a;b] }
s:=s + (1+x); {s:=s +(x*x)}{Вообще можно подставить любую функцию }
delay(10000); {задержка,чтобы произвольные значения не повторялись}
end;{конец испытаний}
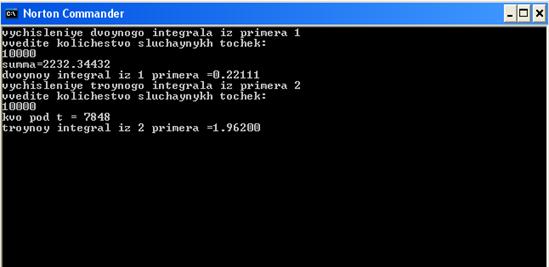
writeln(‘s=’,s);{Сумма функции для n произвольных значений}
Integral:=(1/n)*k*s ;
writeln(‘Интеграл=’,Integral);
readln;
END.
Требуется ввести промежуток интегрирования и количество испытаний, интегрируемая функция уже задана в программе(но ее можно поменять).
3 3
ò(x+1)dx = 6 ; ò (x*x)dx = 9; (По методу Ньютона-Лейбница).
1
| Функция | k | N= 10 | N= 100 | N= 500 | N= 1000 |
| f(x)=1 + x | 2 | 5.737 | 5.9702 | 6.02 | 5.99 |
| f(x)=x * x | 3 | 9.6775 | 8.528 | 8.7463 | 8.937 |
Похожие работы
... , разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) и по ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...
... значения интеграла, основан на «монотонности» интеграла. При этом способе подынтегральную функцию приближают снизу и сверху интегрируемыми в замкнутом виде функциями и , т.е. , (34) Тогда (35) 5. Вычисление интегралов методом Монте-Карло Пусть нам нужно вычислить интеграл: (36) В случае, когда методы Ньютона-Котеса и Гаусса работают плохо, приходится обращаться к вероятностным ...
... в особенности многомерных, для решения систем алгебраических уравнений высокого порядка, для исследования различного рода сложных систем (автоматического управления, экономических, биологических и т.д.). Сущность метода Монте-Карло состоит в следующем: требуется найти значение а некоторой изучаемой величины. Для этого выбирают такую случайную величину X, математическое ожидание которой а: (1) ...






0 комментариев