Постановка задачи.
Для начала я хочу рассмотреть некоторые понятия и результаты, играющие в дальнейшем основную роль. Рассуждения, которыми мы здесь пользуемся, иногда значительно отличаются от рассуждений в основных книгах по данному вопросу, так как в данной работе мы имеем целью, не давая полных доказательств, сделать для простейших случаев геометрическую ситуацию интуитивно ясной, тогда как позднее мы будем вынуждены жертвовать наглядностью ради точности. В работе рассматривается основная задача геометрии чисел, приводится теорема Минковского с её доказательством, и объясняются такие понятия геометрии чисел как решётки и критические решётки. В конце работы приводится так называемая «неоднородная задача» геометрии чисел.
Основная задача геометрии чисел.
Основной и типичной задачей геометрии чисел является следующая задача.
Пусть f(х1,…,xn) — функция вещественных аргументов, принимающая вещественные значения. Как мал может быть f(u1,…,un) при подходящем выборе целых чисел u1,…,un? Может встретиться тривиальный случай f(0,…,0)=0, например, если f(х1,…,xn) является однородной формой; в этом случае совокупность значений u1 = u2 = ... = un = 0 из рассмотрения исключается (“однородная проблема”).
Обычно рассматриваются оценки, применимые не только для конкретных функций f, но и для целых классов функций. Так, типичным результатом такого рода является следующее предложение. Пусть
f(x1,x2) = a11x12 + 2a12x1x2 + a22x22 (1)
- положительно определённая квадратичная форма. Тогда найдутся такие целые числа u1,u2, не равные одновременно нулю, что справедливо неравенство
f(u1,u2) (4D/3)1/2 (2)
где D = a11a22 – a122 – определитель формы. Ясно, что если этот результат верен, то он является наилучшим. Действительно,
u12 + u1u2 + u22 1
для всех пар целых чисел u1,u2, не равных одновременно нулю; здесь D = 3/4.
Конечно, случай положительно определённых бинарных квадратичных форм крайне прост, и результат задачи был известен задолго до возникновения геометрии чисел. Однако на положительно определённых бинарных квадратичных формах относительно просто проводятся некоторые рассуждения геометрии чисел, так что эти формы удобно использовать в качестве иллюстрации всех рассуждений.
Только что сформулированный результат можно выразить наглядно. Неравенство типа
f(x1,x2) k,
где f(x1,x2) — форма (1), а k — некоторое положительное число, задает область плоскости {x1,x2}, ограниченную эллипсом. Таким образом, наше предложение утверждает, что если k (4D/3)1/2, то область содержит точку (u1,u2) с целыми координатами u1 и u2, не равными одновременно нулю.
Теорема Минковского.
Аналогичный, но, правда, не настолько точный результат немедленно следует из основной теоремы Минковского. В двумерном случае эта теорема утверждает, что область всегда содержит точку (u1,u2) с целыми координатами, отличную от начала, если эта область удовлетворяет следующим трем условиям:
область симметрична относительно начала координат; т. е. если точка (x1,x2) находится в , то точка (-x1,-x2) также содержится в ;
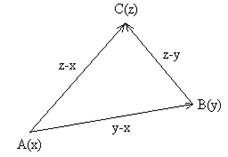
область выпукла; т. е. если (x1,x2), (y1,y2) — две какие-нибудь точки области , то и весь отрезок
{x1 + (1-)y1, x2 + (1-)y2}, 0 1,
соединяющий эти точки, также содержится в ;
3) площадь больше 4.
Любой эллипс f(x1,x2) k удовлетворяет условиям 1) и 2). Так как его площадь равна
k / (a11a22 – a12)1/2 = k / D1/2,
то он удовлетворяет условию 3), если k > 4D1/2. Таким образом, мы имеем результат, аналогичный приведенному выше предложению, если в (2) константу (4/3)1/2 заменить любым числом, большим 4/.
Доказательство теоремы Минковского.
Интересно будет кратко рассмотреть основные идеи, лежащие в основе доказательства теоремы Минковского, потому что в формальных доказательствах, приводимых основными источниками, они заслоняются необходимостью получения сильных теорем, имеющих наиболее широкие приложения.

Вместо области Минковский рассматривает область = /2, которая состоит из точек (x1/2,x2/2), где (x1,x2) точки области . Таким образом, область симметрична относительно начала координат и выпукла, её площадь равна четверти площади области и, следовательно, больше 1. В общем случае Минковский рассматривает совокупность областей (u1,u2) с центрами в целочисленных точках (u1,u2), полученных из тела параллельными переносами.
Для начала справедливо отметить, что если и (u1,u2) пересекаются, то точка (u1,u2) находится в . Обратное утверждение тривиально. Если точка (u1,u2) находится в , то точка (u1/2,u2/2) содержится как в , так и в (u1,u2). Действительно, пусть (ξ1, ξ2) – точка, лежащая в пересечении. Так как точка (ξ1, ξ2) лежит в области (u1,u2), то тогда точка (ξ1 – u1, ξ2 – u2) лежит в области ; следовательно, ввиду симметрии области точка (u1 - ξ1, u2 - ξ2) находится в . Наконец, в силу выпуклости тела середина отрезка, соединяющего точку (u1 - ξ1, u2 - ξ2) с точкой (ξ1, ξ2), то есть точка (u1/2,u2/2), лежит в , а потому точка (u1,u2) находится в . Что, собственно, и требовалось доказать. Ясно, что область (u1,u2) тогда и только тогда пересекается с областью (u1’,u2’), когда область пересекается с областью (u1 - u1’, u2 - u2’).
Таким образом, чтобы теорема Минковского была доказана, достаточно показать, что если области (u1,u2) не пересекаются, то площадь области (u1,u2) не превышает 1. Небольшое размышление убеждает, что так должно быть. Другое обоснование, возможно интуитивно более ясное, можно получить, полагая, что область целиком содержится в квадрате
x1 ≤ X, |x2| ≤ X,
при этом нужно учитывать то, что выпуклая область конечной площади ограничена.
Пусть U — достаточно большое целое число. Существует (2U + 1)2 областей (u1,u2), координаты центров которых удовлетворяют неравенствам
u1 ≤ U, |u2| ≤ U.
Все эти области целиком находятся в квадрате x1 ≤ U + X, |x2| ≤ U + X,
площадь которого равна
4 (U + X)2.
Так как предполагается, что области (u1,u2) не пересекаются, то имеет место неравенство
(2U + 1)2V 4(U + X)2,
где V – площадь области , а значит, и любой области (u1,u2). Устремляя теперь U к бесконечности, мы получаем неравенство V 1, что и требовалось доказать.
Решётки.
Преобразование координат в приведённом примере с определённой бинарной квадратичной формой может привести и к другой точке зрения. Мы можем представить форму f(x1,x2) как сумму квадратов двух линейных форм
f(x1, x2) = Х12 + Х22, (3)
где
Х1 = x1 + x2, X2 = x1 + x2, (4)
,,, - некоторые постоянные вещественные числа. Можно, например, положить
= a111/2, = a11-1/2a12,
= 0, = a11-1/2D1/2.
Обратно, если ,,, - такие вещественные числа, что - 0, и формы Х1, Х2 заданы равенствами (4), то выражениеХ12 + Х22 = a11x12 + 2a12x1x2 + a22x22,
г![]() де
де
a11 = 2 + 2,
a12 = + , (5)
a22 = 2 + 2,
является положительно определенной квадратичной формой с определителем
D = a11a22 – a122 = ( - )2. (6)
Теперь будем рассматривать пару (Х1, Х2) как систему прямоугольных декартовых координат. Тогда говорят, что точки (Х1, Х2), соответствующие целым (x1, x2) в выражениях (4), образуют (двумерную) решетку . В векторных обозначениях решетка есть совокупность точек
(Х1, Х2) = u1(,) + u2(,), (7)
г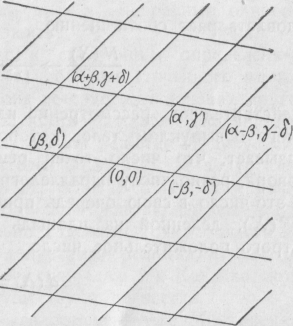 де
u1,
u2 пробегают
все целые числа;
точки (векторы)
(,)
и (,)
образуют базис
решётки .
де
u1,
u2 пробегают
все целые числа;
точки (векторы)
(,)
и (,)
образуют базис
решётки .
Рассмотрим теперь более подробно свойства решеток. Ввиду того, что мы рассматриваем решетку просто как множество точек, мы можем её описать с помощью различных базисов. Например, пара
(α – β, γ – δ), (- β, - δ)
является другим базисом решётки . Фиксированный базис (α, β), (γ, δ) решётки определяет разбиение плоскости двумя семействами равноудалённых параллельных прямых; первое семейство состоит из тех точек (Х1, Х2), которые имеют координаты вида (7), где u2 – любое целое число, а u1 – любое вещественное. Для линий второго порядка семейства u1 и u2 меняются ролями. Таким образом, плоскость разбивается на параллелограммы, вершинами которых являются как раз точки решётки .
Разумеется, что это разбиение зависит от выбора базиса. Однако, можно показать, что площадь получаемых параллелограммов, именно число
|αδ – βγ|,
не зависит от выбора базиса. Это становится возможным, если показать, что число N(X) точек решётки в достаточно большом квадрате
ζ (Х): |Х1| ≤ Х, |Х2| ≤ Х
удовлетворяет соотношению
N(X) / 4X2 → 1 / |αδ - βγ| (X → ∞).
Действительно, рассмотрение идей доказательства теоремы Минковского о выпуклом теле, которое было приведено в кратком виде выше, показывает, что число точек решётки в квадрате ζ (Х), грубо говоря, равно числу параллелограммов, находящихся в этом квадрате. А это число, в свою очередь, приблизительно равно площади квадрата ζ (Х), делённой на площадь |αδ - βγ| одного параллелограмма. Строго положительное число
d () = |αδ - βγ| (8)
называется определителем решётки . Как было только что показано, это число не зависит от выбора базиса.
Критические решётки.
Используя введённые выше новые понятия, можно заметить, что утверждение о существовании целых решений неравенства f(х1,х2) (4D/3)1/2 эквивалентно утверждению о том, что любая решётка в области
Х12 + Х22 ≤ (4/3)1/2 d() (9)
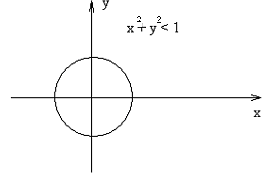
имеет точки, отличные от начала координат. В силу однородности это в свою очередь эквивалентно утверждению, что открытый круг
Đ: Х12 + Х22 < 1 (10)
содержит точку каждой решётки , для которой d() < (3/4)1/2. А тот факт, что существуют такие формы, для которых в (2) знак равенства необходим, эквивалентен существованию решётки с с определителем d(с) = (3/4)1/2, не имеющей точек в круге Đ. Таким образом, задача о произвольной определённой бинарной квадратичной форме эквивалентна задаче о фиксированной области Đ и произвольной решётке. Аналогично исследование решёток с точками в области
| Х1 Х2| < 1
даёт информацию о минимумах inf |f(u1,u2)| неопределённых бинарных квадратичных форм f(x1,x2). Здесь точная нижняя граница берётся по всем целым числам u1 и u2, не равным одновременно нулю. Примеры можно продолжить.
Подобные рассмотрения приводят к следующим определениям. Говорят, что решётка допустима для области (точечного множества) в плоскости {Х1,Х2} если она не содержит никаких других точек , кроме, может быть, начала координат. Последний случай возможен, когда начало координат является точкой области . Тогда мы говорим, что эта решётка -допустима. Точная нижняя грань Δ() определителей d(Λ) всех -допустимых решёток является константой области . Если -допустимых решёток не существует, то полагаем, что Δ() = ∞. Тогда любая решётка Λ, для которой d(Λ) < Δ(), обязательно содержит точку области , отличную от начала координат. -допустимая решётка Λ, для которой d(Λ) = Δ(), называется критической (для ). Конечно, критические решётки, вообще говоря, существуют не всегда.
Важность критических решёток была замечена уже Минковским. Если с – критическая решётка области , а решётка Λ получена из Λс небольшой деформацией (то есть малым изменением пары базисных векторов), то либо решётка Λ имеет точку, отличную от начала координат и лежащую в области , либо d(Λ) ≥ d(Λс). Либо и то, и другое вместе.
В качестве примера можно снова рассмотреть открытый круг
Đ: Х12 + Х22 < 1.
Предположим, что Λс – критическая решётка области Đ. Ниже будет дан набросок доказательства того, что если критическая решётка существует, то она должна иметь три пары точек (А1, А2), (В1, В2), (С1, С2) на границе Х12 + Х22 = 1 круга Đ.
Если Λс не имеет точек на окружности Х12 + Х22 = 1, то можно будет получить Đ-допустимую решетку с меньшим определителем, гомотетически сжимая решетку Λс к началу координат, то есть рассматривая решетку = tΛс точек (tX1, tX2), где (Х1, Х2) Λс , а t — это фиксированное число с условием 0 < t < 1. Тогда d() = t2d(c) < d(c) и, очевидно, будет Đ-допустимой решеткой, если t достаточно близко к 1. Таким образом, решетка c содержит пару точек на окружности Х12 + Х22 = 1, координаты которых после надлежащего поворота осей мы можем считать равными ± (1, 0).
Если бы на окружности Х12 + Х22 = 1 не было бы больше точек решетки c, то мы смогли бы получить Đ-допустимую решетку с меньшим определителем, сжимая решетку c в направлении, перпендикулярном оси X1, то есть принимая за решетку точек (Х1, tХ2), где (Х1, Х2) Λс, а t достаточно близко к 1.
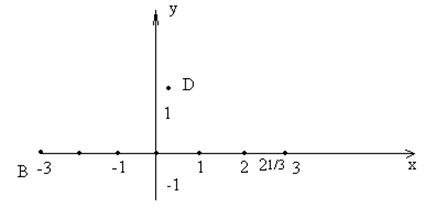
Наконец, если бы Λс имела бы только две пары точек ±(1, 0), ± (В1, В2) на границе, то решетку можно было бы слегка деформировать так, чтобы точка (1, 0) осталась на месте, а точка с координатами (В1, В2) продвинулась бы вдоль окружности Х12 + Х22 = 1 ближе к оси Х1. Наглядно это представлено на рисунке:
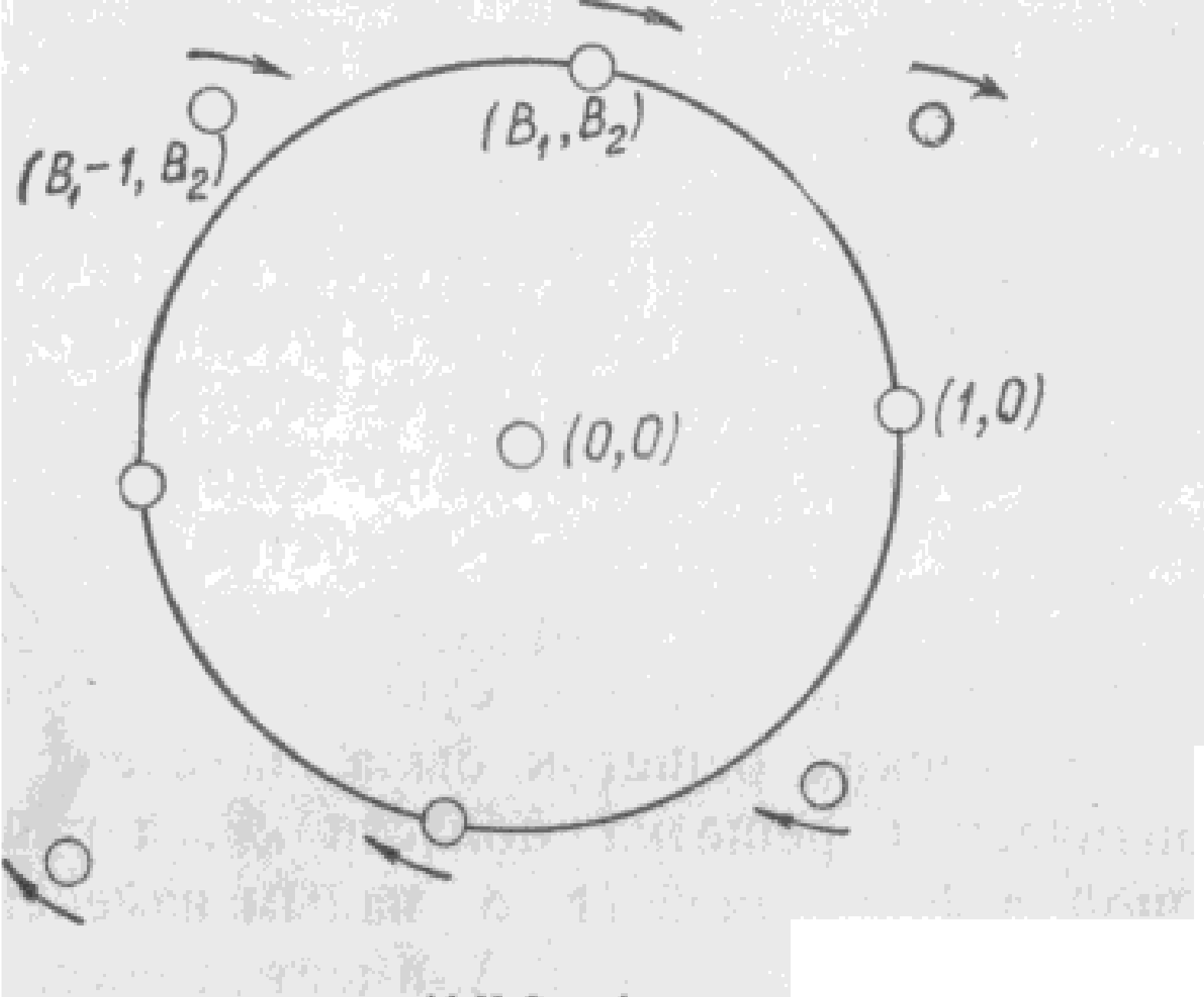
Данная операция, как легко проверить, уменьшает определитель, и при небольших деформациях получающаяся решётка Λ остаётся Đ-допустимой. Действительно, (1,0) и (В1, В2) можно рассматривать как базис решётки Λс, так как треугольник с вершинами (0, 0), (1, 0), (В1, В2), а следовательно, и параллелограмм, отвечающий базису (1, 0), (В1, В2) не содержит внутри себя точек Λс. Тогда критическая решётка Λс (если она существует) должна иметь три пары точек на окружности Х12 + Х22 = 1. Легко увидеть, что единственной решеткой, у которой три пары точек лежат на окружности Х12 + Х22 = 1, а одна из пар есть пара ± (1, 0), является решетка Λ ́ с базисом
(1, 0), (1/2, √3/4).
Она содержит вершины правильного шестиугольника
± (1, 0), ± (1/2, √3/4), ±(-1/2, √3/4),
лежащие на окружности Х12 + Х22 = 1, но не содержит ни одной точки (кроме (0, 0)) в круге Х12 + Х22 < 1. Таким образом, мы показали, что если Đ имеет критическую решетку, то Δ(Đ) = d(Λ ́) = (3/4)1/2. Минковский показал, что критические решетки существуют для довольно широкого класса областей , показав, грубо говоря, что любую -допустимую решетку Λ можно постепенно деформировать до тех пор, пока она не станет критической.
“Неоднородная задача”
Другим общим типом проблемы является следующая типичная «неоднородная задача». Пусть f(х1,…,xn) — некоторая вещественнозначная функция вещественных аргументов х1, . . ., хn. Требуется подобрать постоянное число k со следующим свойством: если ξ1, ..., ξn — любые вещественные числа, то найдутся такие целые числа u1,…,un, что
│f(ξ1 – u1,…, ξn– un)│≤ k.
Подобные вопросы естественно возникают, например, в теории алгебраических чисел. И на этот раз имеется простая геометрическая интерпретация. Для наглядности положим n = 2. Пусть — множество таких точек (х1, х2) двумерной евклидовой плоскости, что
│f(x1, …, xn)│≤ k.
Пусть u1, u2 — любые целые числа; обозначим через (u1, u2) область, полученную из параллельным переносом на вектор (u1, u2); иными словами, (u1, u2) есть множество таких точек х1, х2, что
│f(х1 – u1, х2– u2)│≤ k.
Неоднородная проблема состоит в выборе k таким образом, чтобы области (u1, u2) покрывали всю плоскость. Желательно выбрать k, а значит и , наименьшим из всех возможных (но так, чтобы свойство покрывать всю плоскость сохранилось). Здесь мы имеем противоположность постановке однородной задачи, приведённой выше, где цель состояла в том, чтобы сделать области наибольшими, но все еще не пересекающимися одна с другой.
19
Содержание.
Введение. 2
Постановка задачи. 3
Основная задача геометрии чисел. 4
Теорема Минковского. 6
Доказательство теоремы Минковского. 7
Решётки. 10
Критические решётки. 13
8. «Неоднородная задача». 17
9. Список литературы. 18
2
Список литературы.
Касселс, Дж. В. С. Геометрия чисел – М., Мир, 1965г.
Минковский Г. Геометрия чисел – Лейпциг, 1911г. (переиздание 1996г.)
Марков А. А. О бинарных квадратичных формах положительного определителя – СПб., 1948г.
Чеботарёв М. Г. Заметки по алгебре и теории чисел – УЧ Зап. Каз. Унив-та, 1934г. (переиздание 1994г.)
Чеботарёв М. Г. Доказательство теоремы Минковского о неоднородных линейных формах – М., Мир, 1949г.
19
Министерство Образования Российской Федерации
ГОСУДАРСТВЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ Хабаровский Государственный Педагогический УниверситетКафедра математического анализа и информатики
Курсовая работа
“Геометрия чисел”
Выполнил: =PeppeR=
Научный руководитель: доцент кафедры мат. анализа и информатики
кандидат физ.-мат. наук
Хабаровск -
Похожие работы
... то поймем, как оно устроено, или, грубо говоря, каковы его основные «исходные компоненты». Тогда станет видно, как эти «компоненты» могут сочетаться в иных комбинациях, образуя иные типы пространств. 2.1 Основные понятия описания пространства-времени 2.1.1 Геометрические векторы и линейные операции над ними Для математического описания пространства удобно пользоваться векторами. Этот объект ...
... . Позитивизма. Для позитивистов верным и испытанным является только то, что получено с помощью количественных методов. Признают наукой лишь математику и естествознание, а обществознание относят к области мифологии. Неопозитивизм, Слабость педагогики неопозитивисты усматривают в том, что в ней доминируют бесполезные идеи и абстракции, а не реальные факты. Яркий ...
... объём Vk шара радиуса r в k-пространстве при чётном и нечётном n соответственно равен , (9. 12) Формула (9. 12) дает при k = 2, 3, 4, 5 соответственно , , , (9. 13) Глава III. Применения многомерной геометрии § 10. О необходимости введения многомерного пространства (на примерах задач) В чём состоит польза многомерных пространств? Где они применяются? Зачем понадобилось ...
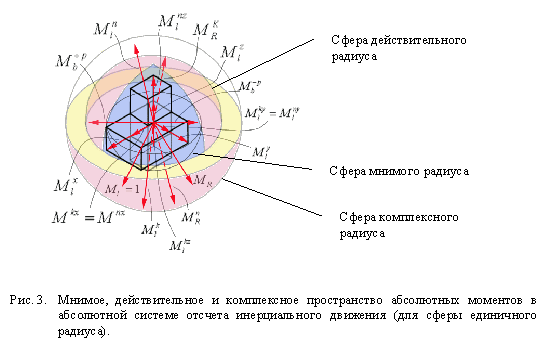
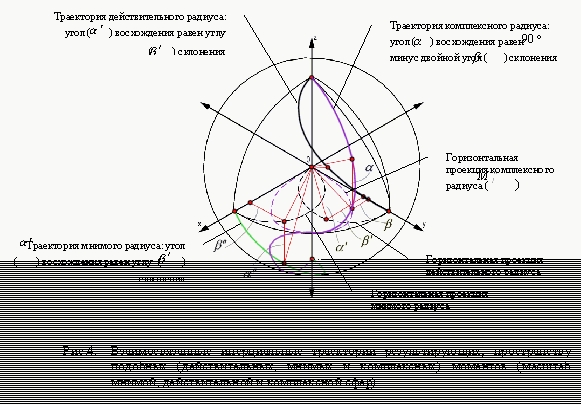
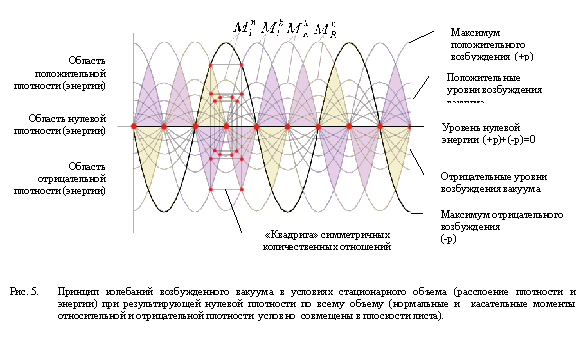
... информационной причинности взаимодействий (нейтрализация энтропии), связанной с процессами отражения степеней упорядоченности (возбуждений), обладание универсальной системой пространственно-временных отношений, выделяют “абсолютный квант” в феноменальное явление физической природы. Он может быть неожиданным материальным воплощением той начальной активной субстанции, которую объективный идеализм, ...




0 комментариев