Навигация
Содержание
Введение………………………..………………………………………………2
1. Построение модели……………………………………………………..6
2. Задача Лагранжа. Безусловный и условный экстремумы……………7
3. Задача Лагранжа с одним ограничением……………………………..11
4. Смысл множителей Лагранжа………………………………………...15
5. Простейшая модель управления запасами…………………………...18
6. Модель I. Модель Уилсона без ограничений……………………..….26
7. Модель II. Модель Уилсона с ограничениями на складские помещения……………………………………………………………...33
8. Рацион Робинзона……………………………………………………...38
9. Взаимные экстремальные задачи……………………………………..42
10. Модель потребительского выбора……………………………………44
11. Лабораторные задачи…………………………………………………..47
12. Заключение……………………………………………………………..51
Список использованной литературы………………………………...………52Введение
Научная модель является отображением некоторых интересующих нас явлений (например, определенных объектов, событий, процессов, систем) и используется в целях управления и предсказания. Основная функция научной модели заключается не в том, чтобы описать явления, а в том, чтобы объяснить их. Модель должна помочь выяснить, каким образом некоторые стороны явления влияют на другие стороны или же на явления в целом. Если построена достаточно верная модель, то эти вопросы можно выяснить, производя соответствующие опыты на модели, не меняя характеристик изучаемого объекта.
Преимущества использования модели для этих целей особенно очевидны, когда опыты на самом объекте или невозможны, как, например, в астрономии, или очень дороги, как в сложных промышленных организациях. Но знание моделей этих далеко не исчерпывается. В самом дели, в некотором смысле научные теории, объясняющие определенные явления, аналогичны моделям этого явления, потому наука не могла бы существовать без моделей, как она не могла бы существовать без теории.
Таким образом, модели играют важнейшую роль в исследовательском процессе и поэтому неизменно возрастает интерес к их изучению. Существующие модели можно разделить на три типа: изобразительные (модели геометрического подобия), модели – аналогии и символические (математические).
Изобразительная модель отображает внешние характеристики системы (как фотография и ли модель самолета). Она подобна оригиналу. Многие фотографии, картины и скульптуры являются изобразительными моделями людей, различных предметов или сцен. Игрушечный автомобиль является изобразительной моделью “настоящего” автомобиля. Глобус является изобразительной моделью земного шара. В общем случае всякое отображение представляет собой изобразительную модель в той мере, в какой его свойства совпадают со свойствами оригинала. Правда, эти свойства обычно подвергаются метрическому преобразованию, т.е. берётся определенный масштаб. Например, глобус имеет уменьшенный диаметр по сравнению с земным шаром, хотя форма и относительные размеры континентов, морей и т.д. приблизительно правильные. Модель атома, наоборот, имеет увеличенные размеры, чтобы его можно было разглядеть не вооруженным глазом. Масштаб в модели вводится для экономии и удобства пользователя. В обычных условиях гораздо легче работать с моделью здания, атома или производственной системы, чем с самим объектом. Так, с опытным заводом, который является уменьшенной моделью полного завода, работать гораздо легче, чем с настоящим заводом.
Изобразительные модели хорошо приспособлены для отображения статического или динамического явления в определенный момент времени. Например, фотография или схема производственных потоков может дать хорошую “картину” работы завода. Но такие модели не подходят для отображения динамики явлений, например для отображения рабочих операций, на заводе. Поэтому они не годятся для изучения изменяющегося процесса, или динамики системы.
Хотя изобразительная модель и подобна оригиналу, она, как и другие типы моделей, отличается от оригинала и не может отразить всех его свойств. В ней отображается только свойства оригинала, существенные для задач, решаемых с помощью данной модели. Этой избирательностью во многом определяется экономичность использования любой научной модели.
Модель – аналог использует ряд свойств одного явления для отображения свойств другого явления (например, в некоторых случаях поток воды через трубы можно принять за аналог “потока” электричества по проводам).
При построении модели различных объектов, событий, процессов или систем не всегда можно простым изменением масштаба изобразить все интересующие нас свойства. Например, мы не можем наглядно представить на глобусе геометрическую структуру Земли. Но мы легко можем представить различные геометрические формации с помощью разноцветной окраски. При этом мы производим подмену одного свойства (цвет) другим (геометрическая структура) в соответствии с некоторыми правилами преобразования. В картографии, например, такое преобразование является узаконенным, причем правила для преобразования приводятся в легенде. В легенде на карте приводится также перечень обозначений: например, сплошная линией обозначается грунтовая дорога, а пунктирной – шоссейная. Такая модель называется моделью – аналогом, поскольку в ней совокупность одних свойств представляется с помощью совокупности других свойств.
Примером простой аналогии является графики. На графиках пользуются расстоянием для отображения таких свойств, как время, число, проценты, вес, и многих других. Графики часто удобны для представления количественных соотношений и дают возможность предсказывать, как изменения одного свойства сказывается на другом свойстве.
Используя модели – аналоги, мы увеличиваем наши возможности проверять на модели изменения различных параметров. Обычно проще изменить модель – аналог, чем изобразительную модель.
Модели – аналоги удобны для отображения динамических процессов или систем. Можно построить модель, работа которой будет аналогична работе конвейера на заводе. Или можно отобразить колебания спроса путем соответствующего изменения некоторой входной величины модели. Однако на изобразительной модели, например уменьшенной действующей модели цеха, такое изменение провести трудно.
Другим преимуществом модели – аналога по сравнению с изобразительной моделью является большая универсальность этой модели. Так, незначительно изменение модели, можно отобразить различные процессы одного класса.
Символическая модель использует символы для отображения свойств изучаемой системы (с помощью математического уравнения или системы уравнений). Элементы модели и их взаимосвязь задаются с помощью символов (обычно математического или логического характера).
Во многих случаях построения моделей – аналогов затруднительно, поскольку изучение динамики явления отнимает много времени. Например, чтобы изучить с помощью аналоговой модели влияния колебания спроса на производственный процесс, нужно проделать на модели много опытов. Если же системы можно представить с помощью математического выражения, то влияние изменить какого-нибудь параметра можно установить с помощью математической дедукции за несколько шагов. Поэтому мы рассматриваем в основном символические модели.
Похожие работы
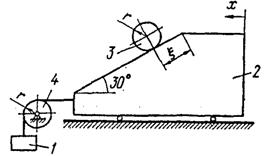
... производные в уравнения Лагранжа (11): или (j=1,2,…, s). (12) Уравнения (12) называются уравнениями Лагранжа второго рода для консервативной системы. 7 Применение уравнений Лагранжа II рода к исследованию движения механической системы Массы тел механической системы m= 2m; m= 6m; m=m. Начальные условия:,,,. Найти уравнения движения системы в обобщенных координатах ,. Для ...
... дифференциальных уравнений в частных производных. В Берлине был подготовлен труд Аналитическая механика (Mecanique analytique), опубликованный в Париже в 1788 и ставший вершиной научной деятельности Лагранжа. В основу всей статики положен т.н. принцип возможных перемещений, в основу динамики – сочетание этого принципа с принципом Д'Аламбера. Введены обобщенные координаты, разработан принцип ...
... от года-x и от номера месяца в году-y следующим образом: F(x)=50-x2+10x-y2+10y. Определите, в каком году и в каком месяце прибыль была максимальной. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету МЕТОДЫ ОПТИМИЗАЦИИ Билет № 22 1) Постановка вариационной задачи с ограничениями. Привести пример. 2) Дайте геометрическую ...
... нахождение точки Куна—Таккера обеспечивает получение оптимального решения задачи нелинейного программирования. Теорему 2 можно также использовать для доказательства оптимальности данного решения задачи нелинейного программирования. В качестве иллюстрации опять рассмотрим пример: Минимизировать при ограничениях С помощью теоремы 2 докажем, что решение является оптимальным. Имеем Так ...
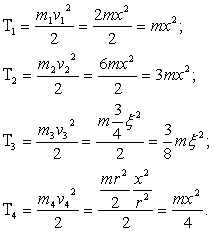
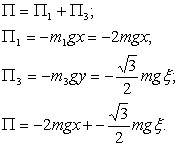
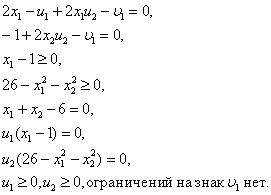
0 комментариев