Навигация
Задача остовных деревьев в k–связном графе
Дипломная работа:
«Задача остовных деревьев в k–связном графе»
работу выполнил
ст. V курса гр.52MI
Жуков В.
Работу приняла:
Dr.физ–мат. наук
Присэкару В.К.
Кишинев–2002
Содержание:
Введение………………………………………………………………………….2
Глава I Основные определения………………………………………………….4
§1 Основные определения теории графов……………………………………...4
§2 Матрицы смежности и инцидентности……………………………………..10
§3 Деревья………………………………………………………………………..13
Глава II Связность ………………………………………………………………18
§4 Вершинная связность и реберная вязность…………………………………18
§5 Двусвязные графы…………………………………………………………....22
§6 Теорема Менгера………………………………………………………….….32
Глава III Выделение k непересекающихся остовных деревьев
2k–реберно связном графе………………………………………………………36
§7 Построение k непересекающихся остовных деревьев………...………...…37
§8
Необходимость
условия
![]() (G)
(G)![]() 2k……………………………………..….40
2k……………………………………..….40
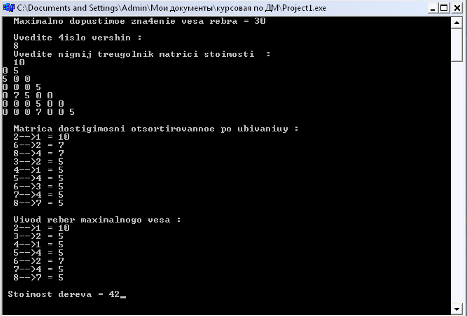
§9 Текст программы……….………………………………………………….…42
Вывод……………………………………………………………………………..51
Введение
Начало теории графов как математической дисциплины было положено Эйлером в его знаменитом рассуждение о Кенигсбергских мостах. Однако эта статья Эйлера 1736 года была единственной в течение почти ста лет. Интерес к проблемам теории графов возродился около середины прошлого столетия и был сосредоточен главным образом в Англии. Имелось много причин для такого оживления изучения графов. Естественные науки оказали свое влияние на это благодаря исследованиям электрических цепей, моделей кристаллов и структур молекул. Развитие формальной логики привело к изучению бинарных отношений в форме графов. Большое число популярных головоломок подавалось формулировкам непосредственно в терминах графов, и это приводило к пониманию, что многие задачи такого рода содержат некоторое математическое ядро, важность которого выходит за рамки конкретного вопроса. Наиболее знаменитая среди этих задач–проблема четырех красок, впервые поставленная перед математиками Де Морганом около 1850 года. Никакая проблема не вызывала столь многочисленных и остроумных работ в области теории графов. Благодаря своей простой формулировке и раздражающей неуловимости она до сих пор остается мощным стимулом исследований различных свойств графов.
Настоящее столетие было свидетелем неуклонного развития теории графов, которая за последние десять – двадцать лет вступила в новый период интенсивных разработок. В этом процессе явно заметно влияние запросов новых областей: теории игр и программирования, теории передачи сообщений, электрических сетей и контактных цепей, а также проблем психологии и биологии.
Вследствие этого развития предмет теории графов является уже обширным, что все его основные направления невозможно изложить в одном томе. В настоящем первом томе предлагаемого двухтомного труда сделан акцепт на основные понятия и на результаты, вызывающие особый систематический интерес.
По теории графов имеется очень мало книг; основной была книга Д. Кёнига (1936), которая для своего времени давала превосходнейшее введение в предмет. Довольно странно, что таких книг на английском языке до сих пор не было, несмотря на то, что многие важнейшие результаты были получены американскими и английскими авторами.
Глава I
Основные понятия§1 Определения.
Предметом первых задач в теории графов были конфигурации, состоящие из точек и соединяющих их линий. В этих рассмотрениях было несущественно, прямые ли это линии или же они являются криволинейными непрерывными дугами, соединяющими две концевые точки, где расположены эти линии, являются ли они длинными или короткими. Существенно только то, что они соединяют две данные точки.
Это
приводит к
определению
графа как
абстрактного
математического
понятия. Рассматривая
множество V,
состоящее из
соединенных
некоторым
образом точек.
Назовем V
множеством
вершин и
элементы
v![]() V–вершинами.
Граф
V–вершинами.
Граф
G=G(V) (1.1)
c множеством вершин V есть некоторое семейство сочетаний, или пар вида
E=(a,
b), a,b![]() V (1.2)
V (1.2)
указывающие, какие вершины являются соседними. В соответствии с геометрическим представлением графа каждая конкретная пара (1.2) называется ребром графа; вершины a и b называются концевыми точками, или концами ребра.
Можно использовать и другой подход. Если даны два множества V1 и V2 то можно образовать множество всех пар
(v1,v2), v1![]() V1, v2
V1, v2![]() V2.
V2.
Это множество пар называется произведением и обозначается через V1V2. В нашем случае каждая пара вершин (a, b) есть элемент произведения VV. Таким образом можно сказать, что граф G из (1.1) с данными ребрами (1.2) есть некоторое подмножество произведения VV.
Это определение графа должно быть дополнено в одном важном отношении. В определении ребра (1.2) можно принимать или не принимать во внимание порядок расположения двух его концов. Если этот порядок несуществен, т.е. если
E=(a, b)=(b, a),
то говорят, что Е есть неориентированное ребро; если же этот порядок существен, то Е называется ориентированным ребром. В последнем случае а называется также начальной вершиной, а b–конечной вершиной ребра Е. Можно также говорить, что Е есть ребро, выходящее из вершины а (отходящее от вершины а, исходящее из вершины а) и входящее в вершину b (подходящее к вершине b, заходящее в вершину b). Как в случае ориентированного, так и в случае неориентированного ребра говорят, что ребро Е из (1.2) инцидентно вершинам a и b, а также что а и b инцидентны Е.
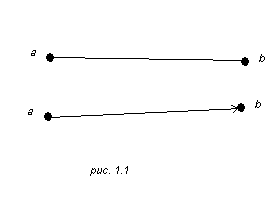
В приложениях граф обычно интерпретируется как сеть, в которой вершинами G являются узлы. Два узла a и b соединяются непрерывной кривой (в частности прямолинейны отрезком) тогда и только тогда, когда имеется пара (1.2). На рисунках узлы будут обозначаться маленькими кружками, а ориентация, если нужно, – стрелкой на представляющей ребро кривой (рис. 1.1).
Граф называется неориентированным, если каждое его ребро не ориентированно, и ориентированным, если ориентированны все его ребра.
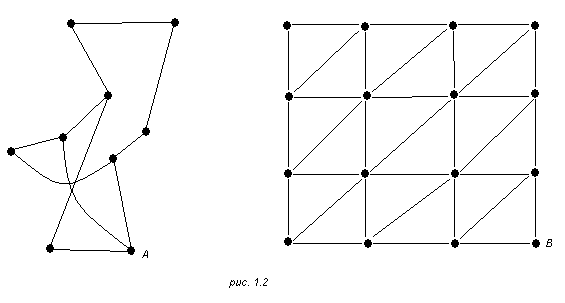
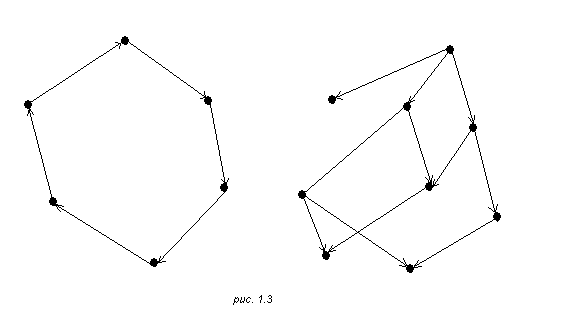
На рис.1.2 приведены примеры неориентированных графов. На рис 1.3 изображены ориентированны графы.
В ряде случаев естественно рассматривать смешанные графы, имеющие как ориентированные, так неориентированные ребра. Например, план города
можно рассматривать как граф, в котором ребра представляют улицы, а вершины – перекрестки; при этом по одним улицам может допускаться лишь одностороннее движение, и тогда на соответствующих ребрах вводится ориентация; по другим улицам движение двустороннее, и на соответствующих ребрах уже никакой ориентации не вводится.
Мы уже отмечали, что при фактическом изображении графа имеется большая свобода в размещении вершин и в выборе формы соединяющих их дуг. Поэтому может оказаться, что один и тот же граф представляется совсем различными чертежами. Будем говорить, что два графа G и G' изоморфны, если существует такое взаимно однозначное соответствие между множествами их вершин V и V’, что вершины соединены ребрами в одном из графов в том и только том случае, когда соответствующие им вершины соединены в другом графе. Если ребра ориентированы, то их направления также должны соответствовать друг другу. На рис 1.2 приведены примеры изоморфных графов, образованных ребрами и вершинами правильных многогранников.
Вершина не инцидентна никакому ребру, называется изолированной. При определение множества вершин V данного графа часто имеет смысл
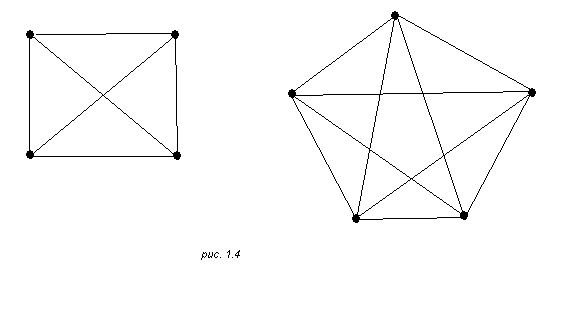
учитывать только неизолированные вершины. Граф, состоящий только из изолированных вершин, называется нуль–графом и может быть обозначен через 0. другим важным случаем является (неориентированный) полный граф
U=U(V), (1.3)
ребрами которого являются всевозможные пары (1.2) для двух различных вершин a и b из V. На рис. 1.4 даны схемы полных графов для множеств вершин из четырех и из пяти элементов.
В ориентированном полном графе U(d) имеются пары ребер, по одному в каждом направлении. Соединяющие любые две различные вершины a и b.
Сформулированное выше определение графа, вместе с соответствующим изображением, достаточно для многих задач. Однако для некоторых целей желательно понятие графа несколько расширить.
В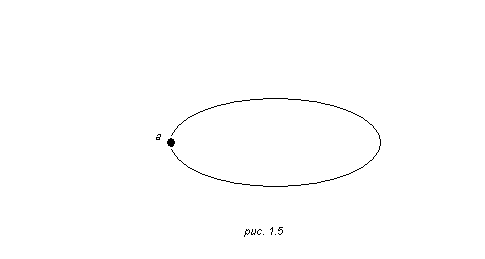 о–первых,
можно получить
ребра, у которых
обе концевые
точки совпадают:
о–первых,
можно получить
ребра, у которых
обе концевые
точки совпадают:
L=(a, a). (1.4)
Такое ребро (1.4) будет называться петлей. При изображении графа петля будет представляться замкнутой дугой, возвращающейся в вершину а и не проходящей через другие вершины (рис 1.5). Петля обычно считается неориентированной. Можно расширить полный граф U в (1.3) до полного графа с петлями U0, добавляя
петлю в каждой вершине, так что ребрами U0 являются все пары (1.2), где допускается и a=b.
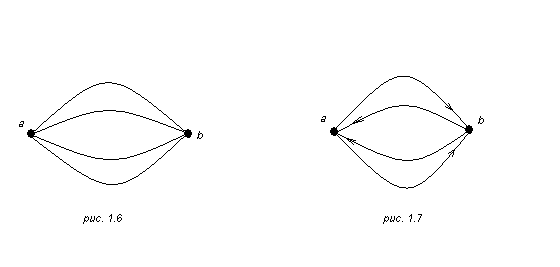
Во–вторых, можно расширить понятие графа, допуская, чтобы пара вершин соединялась несколькими различными ребрами
Ei=(a, b)i, (1.5)
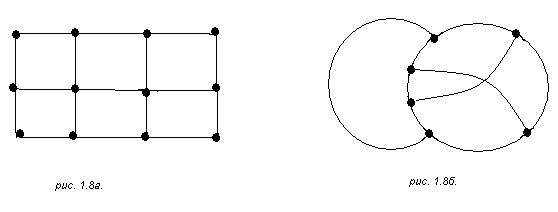
как это изображено на рис. 1.6. Для ориентированного графа две вершины a и b могут соединяться несколькими ребрами в каждом из направлений:
Ei=(a,
b)i, ![]()
![]() =(a,
b)j,
=(a,
b)j,
(рис. 1.7).
Чтобы проиллюстрировать случай, для которого эти понятия оказываются естественными, рассмотрим какое–либо командное соревнование, например турнирную таблицу лиги бейсбола. Вершинами соответствующего графа
являются команды. Пара команд А и В связывается ребром каждый раз, когда они сыграли. Если А выиграла у В, то это ребро будем ориентировать от А к В. а если В выиграла у А, то противоположном направлении; в случае ничьей ребро будет неориентированным.
Для каждого графа G существует обратный граф G*, получаемый изменением ориентации каждого из ребер G на противоположную. Для
каждого ориентированного графа существует также соотнесенный неориентированный граф Gu, ребрами которого являются ребра G, но уже без ориентаций. Иногда удобно превратить неориентированный граф G в ориентированный граф Gd при помощи процесса удвоения, состоящего в замене каждого ребра G парой с теми же концами и приписывании им противоположных ориентаций.
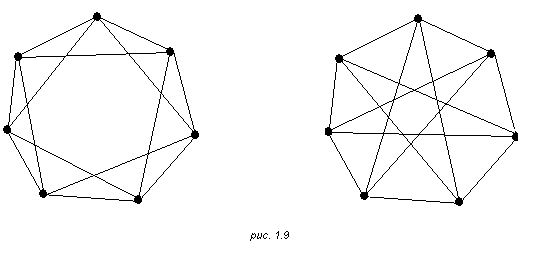
Граф называется плоским, если он может быть изображен на плоскости так что все пересечения ребер являются вершинами G. Граф на рис 1.8а плоский, а на рис 1.8б неплоский.
§2. Матрицы смежности и инцидентности.
В §1 мы определили ребро Е (1.2) графа G (1.1) как элемент или точку (a, b) в произведении VV. Как обычно, элементы этого произведения можно представить в виде клеток квадратной таблицы М с элементами множества V в качестве координат по двум осям (рис 2.1).
В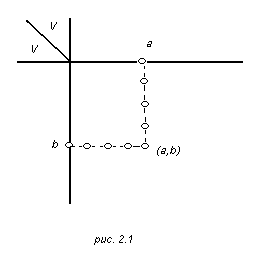 точку с координатами
(a,
b)
поместим числа
1 или 0 в зависимости
от того, существует
или не существует
в G
соответствующее
ребро. Таким
образом, мы
получили конечную
или бесконечную
матрицу
смежности
(вершин)
М(G),
которая полностью
описывает G,
если имеет
однократные
ребра. Обычно
обозначения
выбираются
так, чтобы элементы
(а,
а),
соответствующие
петлям, располагались
на главной
диагонали
матрицы М.
Если G–неориентированный
граф, то ребра
(a,
b)
и
(b,
a)
существуют
одновременно,
таким образом,
неориентированным
графам соответствуют
симметрические
матрицы смежности.
точку с координатами
(a,
b)
поместим числа
1 или 0 в зависимости
от того, существует
или не существует
в G
соответствующее
ребро. Таким
образом, мы
получили конечную
или бесконечную
матрицу
смежности
(вершин)
М(G),
которая полностью
описывает G,
если имеет
однократные
ребра. Обычно
обозначения
выбираются
так, чтобы элементы
(а,
а),
соответствующие
петлям, располагались
на главной
диагонали
матрицы М.
Если G–неориентированный
граф, то ребра
(a,
b)
и
(b,
a)
существуют
одновременно,
таким образом,
неориентированным
графам соответствуют
симметрические
матрицы смежности.
Если G имеет кратные ребра, то числа 0 и 1 в клетках (a, b) можно заменить кратностями (a, b) ребер, соединяющих а и b. Это дает описание графа G матрицей с целыми неориентированными элементами. Обратно, любая такая матрица может быть интерпретирована как граф, так что любые результаты для графов могут быть сформулированы как свойства таких матриц.
Сказанное приводит к дальнейшему расширению понятия графа, использующему уже все конечные или бесконечные матрицы, элементами которых являются вещественные неотрицательные числа. Такие матрицы встречаются в различных областях математики. Например, стохастические матрицы – в теории вероятностей и в теоретической физике. Где рассматриваемая система имеет некоторое множество V возможных состояний, и любая пара состояний (a , b) связывается некоторой вероятностью перехода (a, b). Другим примером является граф, представляющий схему дорог, в котором (a, b) означает соответствующее расстояние между а и b.
Графы
могут быть
также описаны
матрицами
другого вида.
Всякий граф
состоит из
объектов двух
типов–вершин
и ребер. Можно
построить
матицу M1(G),
строки которой
соответствуют
вершинам, а
столбцы–ребрам.
На месте (а,
Е) в
этой матрице
поместим значение ![]() =1,
если а–начальная
вершина ребра
Е, значение
=-1,
если а–конечная
вершина, и =0,
если а не инцидентно
Е. Если G–неориентированный
граф, то можно
использовать
только значения
=1
и =0.
Эта матрица
M1(G)
называется
матрицей
инцидентности
графа G.
=1,
если а–начальная
вершина ребра
Е, значение
=-1,
если а–конечная
вершина, и =0,
если а не инцидентно
Е. Если G–неориентированный
граф, то можно
использовать
только значения
=1
и =0.
Эта матрица
M1(G)
называется
матрицей
инцидентности
графа G.
Введем, наконец, матрицу смежности ребер I(G), в которой и строки и столбцы отвечают ребрам G. Для простоты предположим. Что G не имеет петель, а ребра неориентированные и однократные. На месте (E, E’) в I(G) поместим =1, если Е и Е’–различные ребра с общим концом, и =0, если Е=Е’ или если они не имеют общего конца. Таким образом, I(G)–квадратная матрица, определяемая графом G.
Можно встать и на другую точку зрения и рассматривать I(G) как матрицу смежности вершин для нового графа, также обозначаемого через I(G), вершинами которого являются ребра Е графа G, а ребрами–пары (E, E’) с =1. Назовем I(G) графом смежности ребер или смежности графом для G. Существование такого графа, в котором бывшие ребра становятся вершинами и наоборот, объясняет двойственность между вершинами и ребрами, встречающуюся в некоторых вопросах теории графов.
Фактическое построение смежности графа I(G) по чертежу графа G просто. На каждом ребре Е выбираем фиксированную точку еЕ, например середину Е. Пару таких вершин (е, е’) соединяем новым ребром, принадлежащим I(G), тогда и только тогда, когда соответствующие ребра Е и Е’ имеют общую вершину в G.
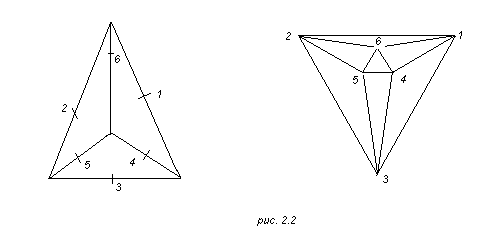
Рис. 2.2 дает это построение для графа тетраэдра; смежностным графом для него является граф октаэдра.
Предположим, то в вершине е сходится (е) ребер Е=(е, е’) из G. Тогда в I(G) середина eE ребра Е соединяется ребрами с (е)–1 серединами остальных ребер из G, имеющих конец в е. Таким образом, в I(G) эти новые ребра образуют новый граф U(e) с (е) вершинами. В I(G) вершина eE соединяется ребрами также с (е’)–1 серединами остальных ребер из G, из имеющих конец в e’, и эти новые ребра образуют другой полный граф U(e’). Два графа U(e) и U(e’) имеют ровно одну общую вершину, именно вершину eE, определяемую единственным ребром Е, соединяющим e и e’. Таким образом, I(G) имеет такое непересекающееся по ребрам разложение
I(G)=![]() 2.1
2.1
На полные графы U(e) с (е) вершинами, что U(e) имеет единственную общую вершину с каждым из (е) других полных графов U(e’). Исключение составляет случай, когда (e, e’)–единственное ребро в e’, т.е. (е’)=1. Тогда не существует графа. U(e’).
Предположим,
что, наоборот,
для графа G1
существует
такое разложение
(2.1) на полные
графы, что пара
(U(e),
U(e’))
имеет не более
одной общей
вершины. Тогда
G1
можно рассматривать
как смежностный
граф G1=I(G)
некоторого
графа G,
считая, что
каждое U(e)
имеет 1![]() (е)
общих вершин
с другими U(e’).
Каждому U(e)
поставим в
соответствие
одну вершину
e
и соединим e
и e’
ребром в G
тогда и только
тогда, когда
U(e)
и
U(e’)
имеют общую
вершину. К этим
ребрам добавим
(е)–
1 ребер (e,
e’’),
идущих к новым
вершинам e’’,
в которых существует
только одно
это ребро.
(е)
общих вершин
с другими U(e’).
Каждому U(e)
поставим в
соответствие
одну вершину
e
и соединим e
и e’
ребром в G
тогда и только
тогда, когда
U(e)
и
U(e’)
имеют общую
вершину. К этим
ребрам добавим
(е)–
1 ребер (e,
e’’),
идущих к новым
вершинам e’’,
в которых существует
только одно
это ребро.
![]() §3
Деревья
§3
Деревья
![]()
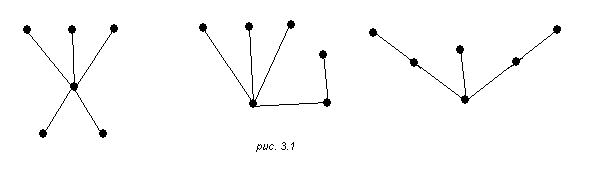
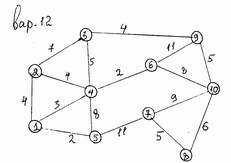
Деревом называется связный граф, не содержащий циклов. Любой граф без циклов называется ациклическим (или) лесом. Таким образом, компонентами леса являются деревья. На рис.12 изображены все деревья шестого порядка.
Существует несколько вариантов определения дерева; некоторые из них отражены в следующей теореме.
Теорема 3.1 Для графа следующие утверждения эквивалентны:
G – дерево;
G – связный граф и m=n-1;
G – ациклический граф и m=n-1;
любые две несовпадающие вершины графа соединяет единственная простая цепь;
G – ациклический граф, обладающий тем свойством, что если каку–либо пару его несмежных вершин соединить ребром, то полученный граф будет содержать ровно один цикл.
1)![]() 2)
Воспользуемся
индукцией по
n.
При n=1
утверждение
трививально.
Пусть n>1,
е
2)
Воспользуемся
индукцией по
n.
При n=1
утверждение
трививально.
Пусть n>1,
е![]() EG.
В дереве G
нет циклов,
следовательно,
согласно лемме
4.1, граф G
– е
имеет ровно
две компоненты
Т1
и Т2,
EG.
В дереве G
нет циклов,
следовательно,
согласно лемме
4.1, граф G
– е
имеет ровно
две компоненты
Т1
и Т2,
каждая из которых есть дерево. Пусть дерево Ti является (ni, mi) – графом, i=1, 2. По индуктивному предположению верно равенство
mi=ni-1. (1)
Далее имеемm=m1+m2+1=(n1-1)+(n2-1)+1=(n1+n2)-1=n-1.
2)
![]() 3)
Граф G
связен и m=n-1.
Нужно доказать,
что в G
нет циклов.
Пусть, напротив,
в графе G
есть цикл и
пусть ребро
е–ребро этого
цикла. Тогда
граф G
– е
связен (лемма
4.8) и имеет n-2
ребра, что
противоречит
теореме 4.9. следовадельно,
G
–ациклический
граф.
3)
Граф G
связен и m=n-1.
Нужно доказать,
что в G
нет циклов.
Пусть, напротив,
в графе G
есть цикл и
пусть ребро
е–ребро этого
цикла. Тогда
граф G
– е
связен (лемма
4.8) и имеет n-2
ребра, что
противоречит
теореме 4.9. следовадельно,
G
–ациклический
граф.
3)
![]() 4)
Пусть к–число
компонент графа
G.
Пусть, далее,
компонента
Тi
является (ni,
mi)–графом.
Так как Тi–дерево,
то верно равенство
(1). Теперь имеем
4)
Пусть к–число
компонент графа
G.
Пусть, далее,
компонента
Тi
является (ni,
mi)–графом.
Так как Тi–дерево,
то верно равенство
(1). Теперь имеем
n-1=m=m1+m2+…+mk=(n1-1)+(n2-1)+…+(nk-1)=(n1+…+nk)-k=n-k;
т.е. к=1. Итак, G–связный граф и потому любые несовпадающие вершины u и v соединены в нем просой цепью. Если бы в G были две несовпадающие простые (u,v)–цепи, то согласно утверждению 4.3 их объединение содержало бы цикл. Следовательно, каждые две вершины соединены единственной простой цепью.
4)
![]() 5)
пара несовпадающих
вершин, принадлежащих
одному циклу,
соединена по
меньшей мере
двумя простыми
цепами. Следовательно,
граф G
ациклический.
Пусть u
и v–две
его нечмежные
вершины. Присоединим
к графу G
ребро e=uv.
В G
есть простая
(u,v)–цепь,
которая в G+e
дополняется
до цикла. В силу
утверждения
4.4 этот цикл
единственный.
5)
пара несовпадающих
вершин, принадлежащих
одному циклу,
соединена по
меньшей мере
двумя простыми
цепами. Следовательно,
граф G
ациклический.
Пусть u
и v–две
его нечмежные
вершины. Присоединим
к графу G
ребро e=uv.
В G
есть простая
(u,v)–цепь,
которая в G+e
дополняется
до цикла. В силу
утверждения
4.4 этот цикл
единственный.
5)
![]() 1)
нужно докакзать,
что граф G
связен. Если
бы вершины u
и v
принадлежали
разным компонентам
графа G,
то граф G+uv
не имел бы циклов,что
потиворечит
утверждению
5). Итак, G
связен и потому
является деревом.
Доказано.
1)
нужно докакзать,
что граф G
связен. Если
бы вершины u
и v
принадлежали
разным компонентам
графа G,
то граф G+uv
не имел бы циклов,что
потиворечит
утверждению
5). Итак, G
связен и потому
является деревом.
Доказано.
Следствие 3.2. В любом дереве порядка n2 имеется неменее двух концевых вершин.
Пусть
d1, d2, …, dn (2)
–степенная последовательность дерева. Тогда
![]()
(лемма о рукопожатиях) и все di>0. Следовательно, хотя бы два числа из последовательности (2) равны 1.
Пусть Н–остовный подграф поизвольного гафа G. Если на каждой области связности графа G графом Н порождает дерево, то Н называется остовом (или каркасом) графа G. очевидно, что в каждом графе существует остов: разрушая в каждой компоненте циклы, т.е. удаляя лишние ребра, придем к остову. Остов в графе легко найти с помощью поиска в ширину.
Следствие 3.3. число ребер произвольного графа G, которые необходимо удалить для получения остова, не зависит от последовательности их удаления и равно m(G)-|G|+k(G), где m(G) и k(G)–число ребер и число компонент графа G соответственно.
Если (n1, m1)–граф Н является одной из компонент графа G, то для превращения ее в остове дерево нужно удалить m1-(n1-1) подходящих ребер. Суммируя по всем k(G) компонентам, получим требуемое.
Число (G)=m(G)-|G|+k(G) называется циклическим рангом (или цикломатическим числом) графа G. число ребер остова графа G называется коциклическим рангом графа G. таким образом.
Очевидны три следствия 13.4–13.6.
Следствие 3.4. Граф G является лесом тогда и только тогда, когда (G)=0.
Следствие 3.5. граф G имеет единственный цикл тогда и только тогда, когда (G)=1.
Следствие 3.6. Граф, в котором число ребер не меньше, чем число вершин, содержит цикл.
Утверждение 3.7. Если S и Т –два остова графа G, то для любого ребра е1 графа S существует такое ребро е2 графа Т, что граф также является остовом.
ДоказательствоНе ограничивая общности, будем считать граф G связным. Граф имеет ровно две области связности; пусть это будут А и В. Поскольку граф Т связен, то в нем существует ребро е2, один из концов которого входит в А, а другой – в В. Граф Н=S-e1+e2 связен и число ребер в нем такое же, как в дереве S. следовательно, он сам является деревом. Итак, Н–остов графа G. Доказано.
Теорема 13.8. Центр любого дерева состоит из одной или из двух смежных вершин.
ДоказательствоОчевидно, что концевые вершины дерева Т являются центральными только для T=K1 или T=K2.
Пусть Т дерево порядка n>2. Удалив из Т все концевые, получим дерево Т’. Очевидно, что эксцентриситет Т на единицу меньше эксцентриситета дерева Т и что центры деревьев Т и Т совпадают. Далее доказательство легео проводится индукцией по числу веншин.Доказано.
Глава II
Связность
Связный граф был определен как граф, у которого любые две вершины соединены цепью. Так, оба графа Кn и Cn связны, однако интуитивно ясно, что при n>3 граф Kn «сильнее» связен, чем Cn. В этой главе вводится и исследуются понятия, характеризующие степень связности графа.
§4 Вершинная связность и реберная связность.
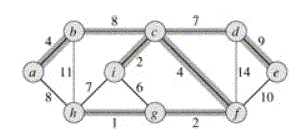
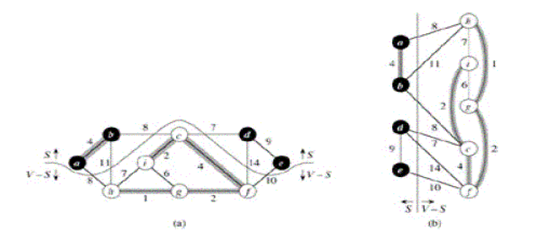
Прежде чем ввести понятия вершинной и реберной связности, рассмотрим одну математическую модель, возникающую, в частности, при проектировании и анализе сетей ЭВМ. Имеется сеть, состоящая из центров хранения и переработки информации. Некоторые пары центров соединены каналами. Обмен информацией между любыми двумя центрами осуществляется либо непосредственно по соединяющему их каналу, если он есть, либо через другие каналы и центры. Сеть считается исправной, если каждая пара центров в состоянии обмениваться информацией. Такой сети естественно сопоставить граф: вершины–центры, ребра–каналы сети. Тогда исправной сети будет соответствовать связный граф. Важным понятием является надёжность (живучесть) сети, под которой обычно подразумевают способность сети функционировать при выходе из строя одного или нескольких центров или (и) каналов. Ясно, что менее надежной следует считать ту сеть, исправность которой нарушается при повреждении меньшего количества элементов. Оказывается, надежность сети можно измерять на основе вводимых ниже определений.
Числом
вершин связности
(или
просто числом
связности)
![]() (G)
графа G
называется
наименьшее
число вершин,
удаление которых
приводит к
несвязному
или одновершинному
графу.
(G)
графа G
называется
наименьшее
число вершин,
удаление которых
приводит к
несвязному
или одновершинному
графу.
Так,
например, ![]() (K1)=0,
(K1)=0,
![]() (Kn)=n–1,
(Kn)=n–1,
![]() (Cn)=2.
(Cn)=2.
Это вполне согласуется с интуитивным представлением том, что при n>3 граф Kn сильнее связен, чем Cn.
Граф
G,
представленный
на рис. 4.1 связен,
но его связность
можно нарушить,
удалив вершину
4. Поэтому ![]() (G)=1.
Если же попытаться
нарушить связность этого графа
путем удаления
ребер (а не вершин),
то придется
удалить не
менее трех
ребер. Например,
G
распадается
на две компоненты
(G)=1.
Если же попытаться
нарушить связность этого графа
путем удаления
ребер (а не вершин),
то придется
удалить не
менее трех
ребер. Например,
G
распадается
на две компоненты
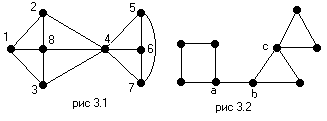
при удалении ребер {4,5}, {4,6}, {4,7}. Чтобы учесть это обстоятельство, введем еще одно определение.
Пусть
G–граф
порядка n>1.
Числом
реберной связности ![]() (G)
графа G
назовем наименьшее
число ребер,
удаление которых
приводит к
несвязному
графу. Число
реберной связности
графа будем
считать равным
нулю, если этот
граф одновершинный.
(G)
графа G
назовем наименьшее
число ребер,
удаление которых
приводит к
несвязному
графу. Число
реберной связности
графа будем
считать равным
нулю, если этот
граф одновершинный.
В
качестве иллюстрации
снова обратимся
к графу G
на рис. 4.1 Здесь ![]() (G)=3
и, следовательно,
(G)=3
и, следовательно,
![]() (G)>
(G)>![]() (G).
Ниже будет
показано, что
противоположное
неравенство
невозможно
ни для какого
графа.
(G).
Ниже будет
показано, что
противоположное
неравенство
невозможно
ни для какого
графа.
Определим некоторые элементы графа, играющие особую роль в дальнейших рассмотрениях.
Вершина v графа G называется точкой сочленения (или разделяющей вершиной), если граф G – v имеет больше компонент, чем G. В частности, если G связен и v – точка сочленения, то G– v не связен. Аналогично ребро графа называется мостом, если его удаление увеличивает число компонент.
Таким образом, точки сочленения и мосты – это своего рода «узкие места» графа. Граф, изображенный на рис. 4.2, имеет три точки сочленения a, b, c и один мост ab.
Понятно, что концевая вершина моста является точкой сочленения, если в графе есть другие ребра, инцидентные этой вершине.
Возвращаясь к рассматриваемой в начале параграфа сети, нетрудно заметить, что число вершинной связности и число реберной связности ее графа отражают чувствительность сети к разрушению центров и каналов соответственно, а мостам и точкам сочленения отвечают наиболее уязвимые места сети.
Если ![]() (G)
– минимальная
степень вершин
графа G,
то очевидно,
что
(G)
– минимальная
степень вершин
графа G,
то очевидно,
что ![]() (G)
(G)![]()
![]() (G),
поскольку
удаление всех
ребер, инцидентных
данной вершине,
приводит к
увеличению
числа компонент
графа.
(G),
поскольку
удаление всех
ребер, инцидентных
данной вершине,
приводит к
увеличению
числа компонент
графа.
Выясним
теперь соотношения
между числами ![]() (G)
и
(G)
и ![]() (G).
Если граф G
не связен или
имеет мост, то
очевидно, что
(G).
Если граф G
не связен или
имеет мост, то
очевидно, что ![]() (G)=
(G)=
![]() (G).
Пусть G–
связный граф
без мостов.
Выберем в этом
графе множество
Е1,
состоящее из
(G).
Пусть G–
связный граф
без мостов.
Выберем в этом
графе множество
Е1,
состоящее из
![]() =
=![]() (G)
ребер, удаление
которых приводит
к несвязному
графу. Пусть
E2
(G)
ребер, удаление
которых приводит
к несвязному
графу. Пусть
E2![]() E1,
|E2|=
E1,
|E2|=![]() –1.
Граф G
– E2
связен и имеет
мост, который
обозначим через
uv.
Для каждого
ребра из множества
Е2
выберем какую–либо
инцидентную
ему вершину,
отличную от
u
и v.
Удалим теперь
выбранные
вершины из
графа. Этим
самым будут
удалены, в числе
прочих, и все
ребра, входящие
в Е2.
Если оставшийся
граф не связен,
то
–1.
Граф G
– E2
связен и имеет
мост, который
обозначим через
uv.
Для каждого
ребра из множества
Е2
выберем какую–либо
инцидентную
ему вершину,
отличную от
u
и v.
Удалим теперь
выбранные
вершины из
графа. Этим
самым будут
удалены, в числе
прочих, и все
ребра, входящие
в Е2.
Если оставшийся
граф не связен,
то ![]() =
=![]() (G)
(G)![]() .
Если же он связен,
то ребро uv
является мостом.
Поэтому удаление
одной из вершин
u
или v
приводит к
несвязному
или одновершинному
графу, а это
означает, что
.
Если же он связен,
то ребро uv
является мостом.
Поэтому удаление
одной из вершин
u
или v
приводит к
несвязному
или одновершинному
графу, а это
означает, что
![]()
![]() .
.
Таким образом, доказана
Теорема 4.1: Для любого графа G верны неравенства
![]() (G)
(G)![]() .
.
Граф
называется
к–связным,
если ![]() ,
и реберно–к–связным,
если
,
и реберно–к–связным,
если
![]() .
Таким образом,
отличный от
К1
граф 1–связен
(односвязен)
тогда и только
тогда, когда
он связен, а
2–связные
(двусвязные)
графы – это
связные графы
без точек сочленения,
не являющиеся
одновершинными.
.
Таким образом,
отличный от
К1
граф 1–связен
(односвязен)
тогда и только
тогда, когда
он связен, а
2–связные
(двусвязные)
графы – это
связные графы
без точек сочленения,
не являющиеся
одновершинными.
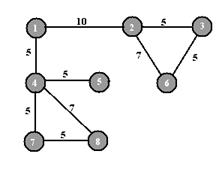
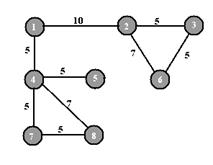
Граф G, изображенный на рис. 4.1 1–связен и реберно–3–связен. Легко видеть, что этот граф содержит подграфы, являющиеся «более связными», чем сам граф. Таков, например, подграф, порожденный множеством вершин {1, 2, 3, 4, 8}. Он 3–связен.
Чтобы учесть эту и подобные ей ситуации, естественно ввести следующее определение: максимальный k–связный подграф графа называется его к–связной компонентой, или просто к–компонентой.
Это определение иллюстрируется на рис. 4.3. На этом рисунке граф G1 имеет две 2–компоненты, а G2–две 3–компоненты. Сами графы G1 и G2
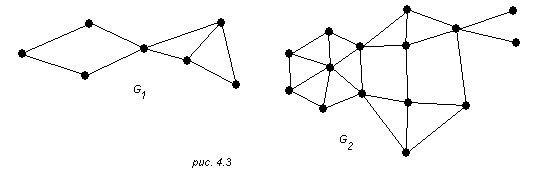
являются
1–компонентами
графа G1![]() G2.
легко заметить,
что 2–компоненты
графа G1
имеют одну
большую вершину,
а 3–компоненты
графа G2–две
общие вершины.
Следующая
теорема показывает,
что это обстоятельство
не случайно.
G2.
легко заметить,
что 2–компоненты
графа G1
имеют одну
большую вершину,
а 3–компоненты
графа G2–две
общие вершины.
Следующая
теорема показывает,
что это обстоятельство
не случайно.
Теорема 4.2: Две различные к–компоненты графа имеют не более чем к–1 общих вершин.
Доказательство
Пусть
G1
и G2
–различные
k–компоненты
графа G
и VG1![]() VG2=X.
Предположим,
что |X|
VG2=X.
Предположим,
что |X|![]() k,
и докажем, что
тогда граф
G1
k,
и докажем, что
тогда граф
G1![]() G2
должен быть
к–связным. Для
этого в данном
случае достаточно
показать, что
он остается
связным после
удаления любых
k–1
вершин, т.е. Y
G2
должен быть
к–связным. Для
этого в данном
случае достаточно
показать, что
он остается
связным после
удаления любых
k–1
вершин, т.е. Y![]() V(G1
V(G1
![]() G2),
|Y|=k-1,
то граф (G1
G2),
|Y|=k-1,
то граф (G1
![]() G2)
– Y
связен. Положим
G2)
– Y
связен. Положим
Yi=(VGi\X) ![]() Y, i=1,2, Y3=X
Y, i=1,2, Y3=X![]() Y.
Y.
Ясно, что
|Yi|![]() k–1, i=1,2,3, Y=Y1
k–1, i=1,2,3, Y=Y1![]() Y2
Y2![]() Y3.
Y3.
|Yi![]() Y3|
Y3|![]() k–1, i=1,2,
k–1, i=1,2,
и графы G1 и G2 k–связны, то графы
Hi=Gi–(Yi![]() Y3), i=1,2,
Y3), i=1,2,
связны.
Так как по
предложению
|X|![]() k,
то X\Y3
k,
то X\Y3![]() Ш,
т.е. связны графы
H1
и H2имеют
хотя бы одну
общую вершину.
Следовательно,
связен граф
H1
Ш,
т.е. связны графы
H1
и H2имеют
хотя бы одну
общую вершину.
Следовательно,
связен граф
H1![]() H2=(G1
H2=(G1![]() G2)–Y.
Последнее
означает, что
граф G1
G2)–Y.
Последнее
означает, что
граф G1![]() G2
k–связен.
Поэтому, вопреки
предположению,
ни G1
не являются
k–компонентами
графа G.
G2
k–связен.
Поэтому, вопреки
предположению,
ни G1
не являются
k–компонентами
графа G.
§5 Двусвязные графы
Случаям, когда k=2 или k=3, в теории графов отведена особая роль. Это объясняется следующими причинами. Во–первых. 2– и 3–связные графы фигурируют во многих теоретических и прикладных вопросах, в частности, ряд задач достаточно уметь решать для 2–связных компонент. Во–вторых, при к=3 и, особенно, при к=2 удается дать в некоторой степени обозримое описание соответствующих графов.
Рассмотрим вначале некоторые простые свойства 2–связных графов, вытекающие непосредственно из определений:
степени вершин 2–связного графа больше единицы;
если графы G1 и G2 2–связны и имеют не менее двух общих вершин, то граф G1![]() G2 также 2–связен;
G2 также 2–связен;
если граф G 2–связен и Р–простая цепь, соединяющая две его вершины, то граф G![]() P также 2–связен;
P также 2–связен;
если вершина v не является точкой сочленения связного графа, то любые две его вершины соединены цепью, не содержащей v; в частности, в 2–связном графе для любых трех несовпадающих вершин a, b, v имеется (a, b)–цепь, не проходящая через v.
Этими свойствами мы будем пользоваться без каких–либо пояснений и дополнительных ссылок на них.
Теорема 5.1 пусть G–связный граф и |G|>2. Тогда следующие утверждения эквивалентны:
граф 2–связен;
любые две вершины графа принадлежат простому циклу;
любая вершина и любое ребро принадлежат простому циклу;
любые два ребра принадлежат простому циклу;
для любых двух вершин a и b и любого ребра е существует простая (a,b)–цепь, содержащая е;
для любых трех вершин a,b,c существует простая (a,b)–цепь, проходящая через с.
1)![]() 2).
Пусть a
и b–две
вершины графа
G.
Рассмотрим
множество всех
простых циклов
графа G,
содержащих
а.
Обозначим через
U
множество всех
вершин, входящих
в эти циклы.
Ясно, что U
2).
Пусть a
и b–две
вершины графа
G.
Рассмотрим
множество всех
простых циклов
графа G,
содержащих
а.
Обозначим через
U
множество всех
вершин, входящих
в эти циклы.
Ясно, что U![]() Ш.
Действительно,
простой цикл,
содержащий
а,
можно получить,
объединить
два ребра ax
и ay
(x≠y)
и простую (x,
y)–цепь,
не проходящую
через а
(существующую
согласно свойству
4)). Предположим,
что b
Ш.
Действительно,
простой цикл,
содержащий
а,
можно получить,
объединить
два ребра ax
и ay
(x≠y)
и простую (x,
y)–цепь,
не проходящую
через а
(существующую
согласно свойству
4)). Предположим,
что b![]() U,
и положим
U,
и положим ![]() =VG\U.
Поскольку граф
G
связен, то в
нем найдется
такое ребро
zt,
что z
=VG\U.
Поскольку граф
G
связен, то в
нем найдется
такое ребро
zt,
что z![]() U,
t
U,
t![]()
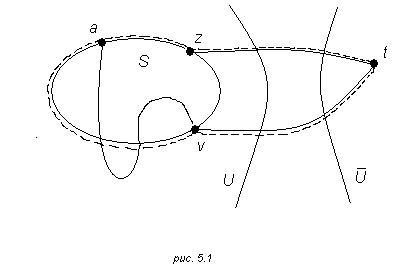
![]() (рис.
5.1). Пусть S–простой
цикл, содержащий
a
и z.
Так как G
– 2-связный
граф, то в нем
имеется простая
(a,
t)-цепь
P,
не содержащая
z.
Пусть v
– первая, считая
от t,
вершина, входящая
в S,
т.е. (t,
v)-подцепь
цепи P
не имеет с S
общих вершин,
отличных от
v.
Теперь легко
построить
простой цикл,
содержащий
a
и t.
Он получается
объединением
(v,
z)-
цепи, проходящей
через а
и являющейся
частью S,
с ребром zt
и (t,v)-подцепью
цепи Р
(на рис. 5.1 этот
цикл показан
пунктирной
линией). Следовательно,
t
(рис.
5.1). Пусть S–простой
цикл, содержащий
a
и z.
Так как G
– 2-связный
граф, то в нем
имеется простая
(a,
t)-цепь
P,
не содержащая
z.
Пусть v
– первая, считая
от t,
вершина, входящая
в S,
т.е. (t,
v)-подцепь
цепи P
не имеет с S
общих вершин,
отличных от
v.
Теперь легко
построить
простой цикл,
содержащий
a
и t.
Он получается
объединением
(v,
z)-
цепи, проходящей
через а
и являющейся
частью S,
с ребром zt
и (t,v)-подцепью
цепи Р
(на рис. 5.1 этот
цикл показан
пунктирной
линией). Следовательно,
t![]() ;
но это противоречит
выбору ребра
zt.
Таким образом,
;
но это противоречит
выбору ребра
zt.
Таким образом,
![]() =Ш,
т.е. a
и b
лежат на общем
простом цикле.
=Ш,
т.е. a
и b
лежат на общем
простом цикле.
2)![]() 3).
Пусть а–вершина
и zt–ребро
графа G.
По условию G
содержит цикл
S,
проходящий
через вершины
a
и z.
Не теряя общности
будем считать,
что zt
3).
Пусть а–вершина
и zt–ребро
графа G.
По условию G
содержит цикл
S,
проходящий
через вершины
a
и z.
Не теряя общности
будем считать,
что zt![]() S.
Если при этом
окажется, что
S
проходит через
вершину t,
то требуемый
цикл строится
очевидным
образом. Пусть
S
не проходит
через t.
Тогда рассмотрим
простой цикл
S',
проходящий
через вершины
t
и a.
Такой цикл, по
условию, существует.
Частью этого
цикла является
простая цепь
Р,
соединяющая
t
с некоторой
вершиной v
S.
Если при этом
окажется, что
S
проходит через
вершину t,
то требуемый
цикл строится
очевидным
образом. Пусть
S
не проходит
через t.
Тогда рассмотрим
простой цикл
S',
проходящий
через вершины
t
и a.
Такой цикл, по
условию, существует.
Частью этого
цикла является
простая цепь
Р,
соединяющая
t
с некоторой
вершиной v![]() S.
Цепь Р
можно выбрать
так, чтобы
S.
Цепь Р
можно выбрать
так, чтобы
VP![]() VS={v}.
искомый цикл
теперь строится
точно так же,
как в предыдущем
пункте.
VS={v}.
искомый цикл
теперь строится
точно так же,
как в предыдущем
пункте.
3)![]() 4).
Пусть ab
и tz–два
ребра графа
G.
По условию G
имеет простые
циклы S
и S',
первый из которых
содержит ab
и z,
а второй – ab
и t.
Далее искомый
цикл строится
так же, как в
предыдущих
пунктах.
4).
Пусть ab
и tz–два
ребра графа
G.
По условию G
имеет простые
циклы S
и S',
первый из которых
содержит ab
и z,
а второй – ab
и t.
Далее искомый
цикл строится
так же, как в
предыдущих
пунктах.
4)![]() 5).
Пусть a,b
5).
Пусть a,b
![]() VG,
tz
VG,
tz![]() EG.
Будучи
связным, граф
G
содержит простую
цепь P=(a,x,…,b).
Согласно утверждению
4) а графе G
есть простой
цикл S,
содержащий
ребра ax,
tz.
Легко видеть,
что в объединении
S
EG.
Будучи
связным, граф
G
содержит простую
цепь P=(a,x,…,b).
Согласно утверждению
4) а графе G
есть простой
цикл S,
содержащий
ребра ax,
tz.
Легко видеть,
что в объединении
S![]() P
имеется требуемая
цепь.
P
имеется требуемая
цепь.
5)![]() 6).
Пусть
a,b,c
6).
Пусть
a,b,c![]() VG,
cd
VG,
cd![]() EG.
По
условию в графе
имеется простая
(a,b)–цепь,
проходящая
через cd
и,
следовательно,
содержащая
c.
EG.
По
условию в графе
имеется простая
(a,b)–цепь,
проходящая
через cd
и,
следовательно,
содержащая
c.
6)![]() 1).
Пусть v
1).
Пусть v![]() VG.
Покажем. Что
граф G
– v
связен, т.е. любая
a,b
его вершин
соединена
цепью. Действительно,
согласно утверждению
6) в графе G
имеется простая
(v,b)-цепь,
которая, очевидно,
не проходит
через v
и, следовательно,
является (a,
b)-цепью
и в графе G
– v.
Доказано.
VG.
Покажем. Что
граф G
– v
связен, т.е. любая
a,b
его вершин
соединена
цепью. Действительно,
согласно утверждению
6) в графе G
имеется простая
(v,b)-цепь,
которая, очевидно,
не проходит
через v
и, следовательно,
является (a,
b)-цепью
и в графе G
– v.
Доказано.
Если в формулировке теоремы 34.1 заменить всюду слова «простая цепь» и «простой цикл» соответственно на слова «цепь» и «цикл», то получим аналогичную теорему о 2–реберно–связном графах.
Как отмечалось выше, при решении многих задач на графах достаточно уметь решать эти задачи для каждой 2–связной компоненты графа. Поэтому представляет интерес взаимное расположение 2–компонент в графе.
Максимальные относительное включения элементы множества связных подграфов графа G, не имеющих точек сочленения, называются его блоками. Таким образом, каждый блок графа либо 2–связен, либо совпадает с К2 или К1 (граф К1– блок тогда и только тогда, когда он является связной компонентой). Связный граф без точек сочленения также называют блоком.
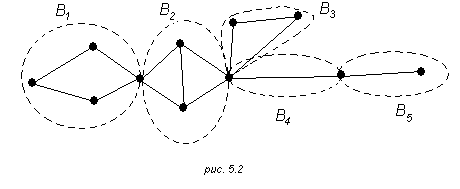
Множество вершин блока будем называть блоковым множеством.
Например, граф, изображенный на рис. 5.2, содержит пять блоков Bi (i=1,2,3,4,5) (они обведены пунктирными линиями). Среди этих блоков В1, В2 и В3 –2-связные графы, а каждый из двух оставшихся является ребром.
Утверждение 5.2. Любые два блока графа имеют не более одной общей вершины. В частности, всякое ребро графа входит только в один его блок.
Утверждение 5.3. Если блок графа содержит вершины a и b, то он содержит и всякую простую (a, b)-цепь этого графа.
Эти утверждения непосредственно следуют из перечисленных в начале параграфа свойств 2–связных графов и теоремы 5.1.
Следствие 5.4. Система блоковых множеств графа является покрытием множеств его вершин. Каждая пара блоковых множеств либо не пересекаются, либо имеют единственную общую вершину, и эта вершина является точкой сочленения графа.
Следующая
конструкция
дает представление
о структуре
графа «с точностью
до блоков».
Пусть В=В{Bi}
и С={ci}
– соответственно
множества
блоков и точек
сочленения
графа G.
Сопоставим
с G
граф bc(G),
у которого B![]() C
– множество
вершин и {Bici:
B
C
– множество
вершин и {Bici:
B![]() B,
ci
B,
ci![]() C,
ci
C,
ci![]() Bi}
– множество
ребер. Тем самым,
ребра двудольного
графа bc(G)
указывают на
принадлежность
точек сочленения
блоками. На
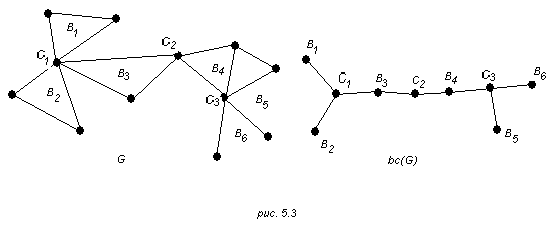
рис. 5.3 представлены
графы G
и bc(G).
Bi}
– множество
ребер. Тем самым,
ребра двудольного
графа bc(G)
указывают на
принадлежность
точек сочленения
блоками. На
рис. 5.3 представлены
графы G
и bc(G).
Утверждение 5.5. Если граф G связен, то bc(G)–дерево.
Доказательство:
Очевидно, что из связности графа G вытекает связность графа bc(G).
Предположим,
что bc(G)
содержит цикл
С.
Пусть этот цикл
имет вид С=(c![]() ,
b
,
b![]() ,c
,c![]() ,
b
,
b![]() ,…,c
,…,c![]() ,b
,b![]() ,c
,c![]() ).
Каждый из блоков
B
).
Каждый из блоков
B![]() содержит (с
содержит (с![]() ,с
,с![]() )-
цепь и объединение
этих цепей дает
простой цикл
в графе G.
Обозначим этот
цикл через С'.
Ясно, что С'
содержит по
крайне мере
две вершины
каждого из
блоков B
)-
цепь и объединение
этих цепей дает
простой цикл
в графе G.
Обозначим этот
цикл через С'.
Ясно, что С'
содержит по
крайне мере
две вершины
каждого из
блоков B![]() .
Поэтому из
утверждения
34.3 следует, что
цикл С'
должен содержаться
в каждом их
этих блоков.
Последнее
означает, что
каждая пара
блоков B
.
Поэтому из
утверждения
34.3 следует, что
цикл С'
должен содержаться
в каждом их
этих блоков.
Последнее
означает, что
каждая пара
блоков B![]() имеет не менее
|C'|
имеет не менее
|C'|
Похожие работы
... Если граф G несвязный, он не может иметь остовного дерева, но у него есть остовный лес. Также можно изменить алгоритм нахождения остовного дерева максимального веса, чтобы на выходе получать минимальный остовный лес. остовное дерево алгоритм краскал В алгоритме Краскала используется жадный подход к решению задачи, т.е. в любой момент выполнения данных алгоритмов существует множество ребер E’, ...
... вес 37). Такое дерево не единственно: заменяя ребро (Ь, с) ребром (а,h), получаем другое дерево того же веса 37. Мы рассмотрим два способа решения задачи о минимальном покрывающем дереве: алгоритмы Крускала и Прима. Каждый их них легко реализовать со временем работы O(E logV), используя обычные двоичные кучи. Применив фибоначчиевы кучи, можно сократить время работы алгоритма Прима до O(E+V logV) ...
... источником новой волны и т.д. При этом необходимо позаботиться о том, чтобы не вернутся в ту вершину, в которой уже были. Для реализации алгоритма понадобятся: матрица m[1..n, 1..n] - матрица смежности графа; вспомогательный массив queue[1..n], в котором будет формироваться очередь, т.е. тип данных первый вошел – первый вышел (FIFO). Размер его достаточен, так как мы не посещаем вершины дважды. ...
... , "базовые" алгоритмы: поиск путей, определение компонент связности графа и т.д. 8. Ввод/вывод графов Одной из проблем при создании средств работы с помеченными графами является выбор внешнего файлового формата для хранения графов. До недавнего времени каждая программная система использовала свой собственный, уникальный формат, что приводило к сложностям при организации обмена данными. ...

0 комментариев