Навигация
Общих вершин. Получаем противоречие с утверждением 5.2. доказано
Граф bc(G) называется bc–деревом связного графа G.
Блоки графа G, соответствующие концевым вершинам его bc–дерева, называются концевыми блоками.
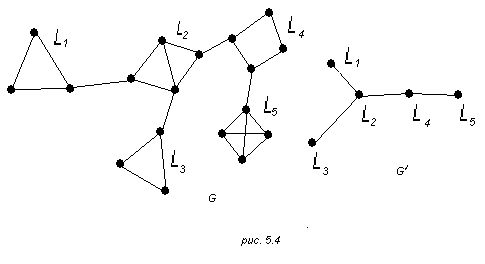
Похожее представление графа можно получить, положив в основу его максимальные реберно-2-связные подграфы, т.е. максимальные связные подграфы, не содержащие мостов. Такие подграфы называют листами. Не останавливаясь на деталях заметим следующее. Каждая вершина графа порядка n>1 принадлежит в точности одному листу и каждое ребро, не являющееся мостом, входит только в один лист. Таким образом, граф состоит из листов и мостов, соединяющих некоторые из них. Для описания строения графа «с точностью до листов» можно ввести граф, аналогичный графу bc(G). Вершины такого графа биективно соответствуют листам графа G и две его вершины соединены ребром в том и только в том случае, когда соответствующая пар листов в G соединена мостом. Можно показать, что введенный таким образом граф является деревом, если исходный граф связен.
На рис. 5.4 граф G имеет 5 листов L1, L2, L3, L4, L5 и 4 моста, а граф G' показывает, как связаны между собой листы графа G.
Приведем некоторые результаты о трехсвязных графах, которые будут использованы в главе «Планарность».
Пусть G–связный граф, H–некоторый его подграф. Простую открытую цепь . графа G назовем H–цепь, если выполняются условия
v1![]() VH,
vk
VH,
vk![]() VH,
vi
VH,
vi![]() VH,
i=
VH,
i=![]()
ребро
e=uv
графа G
также будем
называть Н–цепь,
если u![]() VH,
v
VH,
v![]() VH,
e
VH,
e![]() EH.
EH.
Лемма 5.6. Пусть G–двусвязный граф. Тогда для всякого его подграфа Н, содержащего более одной вершины и отличного от G, существует Н–цепь графа G.
ДоказательствоЕсли Н–остовный подграф, то любое ребро графа G, не входящее в EH, служит Н–цепью.
Пусть
подграф не
является остовным.
Рассмотрим
три попарно
различные
вершины u![]() VH,
v
VH,
v![]() VH,
w
VH,
w![]() VH.
По теореме 5.1
в графе G
есть проcтая
(u,v)
– цепь, проходящая
через w.
Очевидно
существование
подцепи этой
цепи, являющейся
Н
–
цепью графа
G.
Доказано.
VH.
По теореме 5.1
в графе G
есть проcтая
(u,v)
– цепь, проходящая
через w.
Очевидно
существование
подцепи этой
цепи, являющейся
Н
–
цепью графа
G.
Доказано.
Ниже
для u,v![]() VG
положим Guv=
G-u-v.
VG
положим Guv=
G-u-v.
Теорема 5.7. Во всяком 3-связном графе G есть такое ребро uv, что граф Guv не имеет точек сочленения.
Доказательство
Если
|G|=n=4,
то утверждение
теоремы очевидно
. Поэтому будем
считать, что
n![]() 5.
Предположим
противное, т.е.
что для любого
ребра uv
5.
Предположим
противное, т.е.
что для любого
ребра uv![]() EG
граф Guv
имеет хотя бы
одну точку
сочленения.
Тогда на 3-связности
графа G
следует, что
при любом выборе
ребра uv
EG
граф Guv
имеет хотя бы
одну точку
сочленения.
Тогда на 3-связности
графа G
следует, что
при любом выборе
ребра uv![]() EG
граф Guv
обладает следующими
свойствами
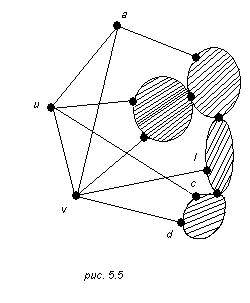
(рис. 5.5):
EG
граф Guv
обладает следующими
свойствами
(рис. 5.5):
если а – висячая вершина графа Guv, то av![]() EG, au
EG, au![]() EG;
EG;
всякий висячий блок графа Guv, не являющийся ребром , содержит такую пару вершин с и d, отличных от точек сочленения графа Guv, что uc![]() EG, vd
EG, vd![]() EG.
EG.
всякий блок графа Guv, имеющий ровно две точки сочленения и отличный от ребра, содержит такую вершину l, не являющуюся точкой сочленения графа Guv, что или ul![]() EG.
EG.
Обозначим через Buv максимальный по числу вершин блок графа Guv, а через tuv– число вершин в этом блоке . Теперь выберем ребро uv так, чтобы число tuv было наибольшим.
Покажем,
что в этом случае
tuv![]() 3.
Пусть tuv=2
и а
– висячая вершина
графа Guv
(являющегося
деревом). Так
как n
3.
Пусть tuv=2
и а
– висячая вершина
графа Guv
(являющегося
деревом). Так
как n![]() 5,
то существует
ребро cd
5,
то существует
ребро cd![]() EGuv.
Из свойства
1) вытекает, что
в графе Gcd
существует
цикл (u,a,v,u),
т.е. tcd>tuv.
Получено
противоречие,
следовательно,
tuv
EGuv.
Из свойства
1) вытекает, что
в графе Gcd
существует
цикл (u,a,v,u),
т.е. tcd>tuv.
Получено
противоречие,
следовательно,
tuv![]() 3.
3.
Через Duv обозначим bc-дерево графа Guv и рассмотрим следующие случаи.
Дерево Duv не является цепью. Выберем в этом дереве цепь, соединяющую пару висячих вершин и проходящую через вершину, соответствующую блоку Buv. Этой цепи соответствует последовательность B1,…,Bp блоков графа Guv, среди которых содержится блок Buv, причем блоки B1 и Bp являются висячими (рис. 5.6).
Пусть
B'– произвольный
висячий блок
графа Guv,
отличный от
B1 и Bp.
Из свойств 1) и
2) вытекает
существование
таких отличных
от точек сочленения
графа Guv
вершин a![]() VB1,
b
VB1,
b![]() VBp,
c
VBp,
c![]() VB',
uc
VB',
uc![]() EG,
va
EG,
va![]() EG,
vb
EG,
vb![]() EG.
Тогда в графе
Guc
вершины множества
EG.
Тогда в графе
Guc
вершины множества
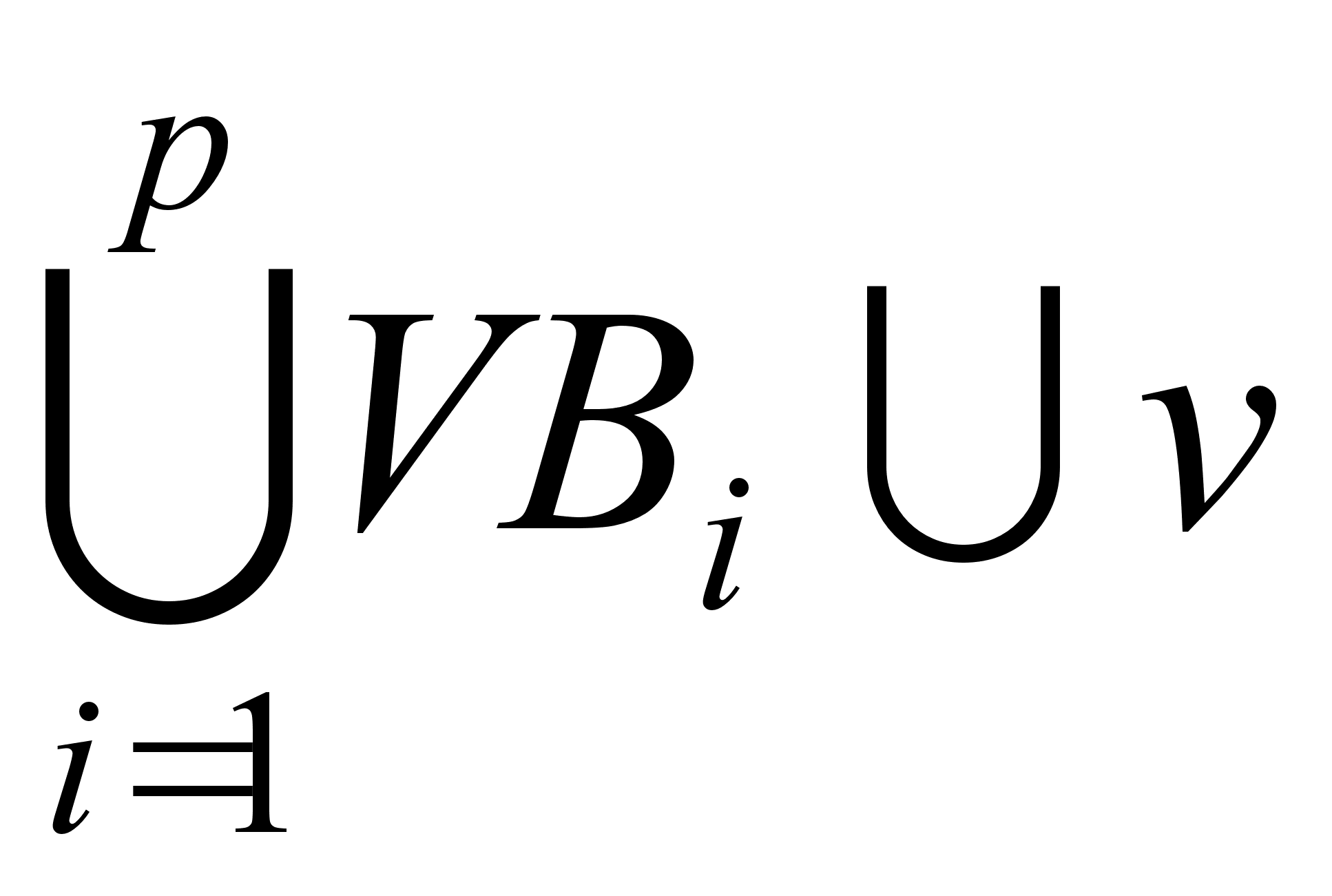 входят в один
блок и, следовательно,
tuv
входят в один
блок и, следовательно,
tuv
Похожие работы
... Если граф G несвязный, он не может иметь остовного дерева, но у него есть остовный лес. Также можно изменить алгоритм нахождения остовного дерева максимального веса, чтобы на выходе получать минимальный остовный лес. остовное дерево алгоритм краскал В алгоритме Краскала используется жадный подход к решению задачи, т.е. в любой момент выполнения данных алгоритмов существует множество ребер E’, ...
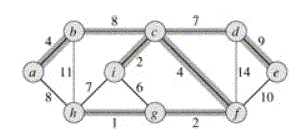
... вес 37). Такое дерево не единственно: заменяя ребро (Ь, с) ребром (а,h), получаем другое дерево того же веса 37. Мы рассмотрим два способа решения задачи о минимальном покрывающем дереве: алгоритмы Крускала и Прима. Каждый их них легко реализовать со временем работы O(E logV), используя обычные двоичные кучи. Применив фибоначчиевы кучи, можно сократить время работы алгоритма Прима до O(E+V logV) ...
... источником новой волны и т.д. При этом необходимо позаботиться о том, чтобы не вернутся в ту вершину, в которой уже были. Для реализации алгоритма понадобятся: матрица m[1..n, 1..n] - матрица смежности графа; вспомогательный массив queue[1..n], в котором будет формироваться очередь, т.е. тип данных первый вошел – первый вышел (FIFO). Размер его достаточен, так как мы не посещаем вершины дважды. ...
... , "базовые" алгоритмы: поиск путей, определение компонент связности графа и т.д. 8. Ввод/вывод графов Одной из проблем при создании средств работы с помеченными графами является выбор внешнего файлового формата для хранения графов. До недавнего времени каждая программная система использовала свой собственный, уникальный формат, что приводило к сложностям при организации обмена данными. ...

0 комментариев