Х – число четное

1.   х – число четное

- число нечетное,

 - число четное Þ F(x) – нечетное.

Значит, -нечетное число, ЧТД.

2.   х – число нечетное

a.   n – нечетное
- число четное,

 - при четном х – четное, значит сумма четна Þ F(x) – четное.

b.   n – четное

- число нечетное,

 - при четном х – четное, значит сумма нечетна Þ F(x) – четное.

Значит, при любом нечетном х, всегда F(x) будет четной при любом (четном/нечетном) значении n Þ

 - четное ЧТД

В результате рассмотренных выше случаев, выводим, что для нечетных - число четное, а для четных  - число нечетное.

ЧТД.

Необычное уравнение

Условие: Для m натуральных через P(m), обозначается произведение всех цифр его десятичной записи, а через S(m) – их сумма. Найти количество k(n) решений уравнения

при n = 2002. Исследуйте величину k(n) решений уравнения.

Решение

Рассмотрим различные случаи числа x.

Пусть в записи х есть ноль, тогда P(x) = 0, значит

Пусть S(x)=y, S(x) = n и в записи числа есть ноль, тогда

Значит, P(S(x)) = P(y) = 0, т.к. число содержит ноль.

S(S(x))=S(y)=n. Имеется бесконечно много решений.

Т.е. для решения данного уравнения подходят числа, S(S(x)) которых равна n.

Т.к. решений бесконечно много, то имеем множество решений для любых случаев.

Идем от обратного: S(y)=n где, a+b+c+…+f = n, т.е. от перестановки цифр сумма не меняется.

При n = 2002, S(x) = 4, P(S(x)) = 4, S(S(X)) = 4 – .

Рассмотрев решения для данного случая, убеждаемся, что n можно подобрать относительно х или наоборот.

Задание 6 Финального Тура

Найти все функции , для которых выполняется

Решение

Пусть х = 1.

. Заменим f(y) на а, имеем:

. (*)

Проверим полученную функцию.

y = 1, тогда

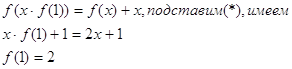
Теперь подставим в исходную функцию.

 

Значит, одно из возможных значений функции - .

Математический Анализ

Условие: Рассматриваются различные непрерывно дифференцируемые функции  (это значит, что для произвольного , существует ), причем функция g непрерывна на сегменте [0;1]; под произодными функции f в конечных точках сегмента [0;1] считаются конечные производные соответственно), для которых f(0)=f(1)=0 и 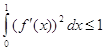. Охарактеризовать множество всех точек, координатной плоскости xOy, через которые могут проходить графики всех функций.

Решение

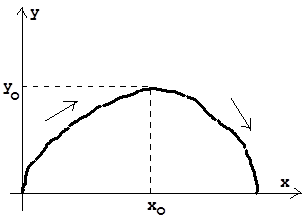Используем неравенство Коши-Буняковского для определенного интеграла, но, прежде, распишем определенный интеграл:

Распишем, также, формулу Ньютона-Лейбница:

 .

Итак,

Значит .

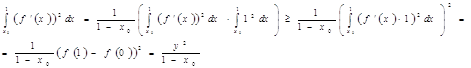
Значит, .

Тогда, .

, т.к.  (по условию).

Рассмотрим два случая:

1. 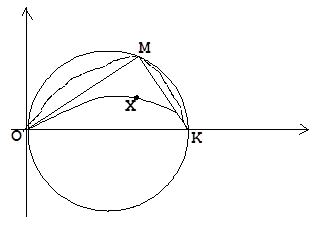  y² = x – x² (точка лежит на контуре)

Т.е. графиком данной функции будет произвольная кривая, в которую вписан угол (угол OMK = 90⁰)

ПРОТИВОРЕЧИЕ !!!

2.  

Т.е. всегда можно построить гладкую кривую, проходящую через точку Х.

Бесконечные Биномиальные Коэффициенты

Условие: упростить выражение .

Решение

Отметим, что если n – четное, что количество членов ряда нечетно, а если n – нечетно, то их количество четно.

Рассмотрим четные и нечетные n.

1.   n = 2k + 1 – нечетное

Тогда, ряд будет иметь вид:

.

Зная, что , упростим этот ряд.

.

Видим, что равноудаленные от концов ряда члены сокращаются, и, т.к. количество их четно, следовательно сумма ряда рана нулю.

, при n = 2k + 1.

2.   n = 2k

Этот случай не был решен до конца, но в результате расчетов первых четных чисел была выведена и проверена, однако не доказана, формула

, где n – четное.

Работа Гончаренко Никиты,

Г. Краматорск, ОШ#35