Исследование свойств прямоугольного тетраэдра

Общеобразовательная муниципальная

средняя школа №5

ИССЛЕДОВАНИЕ СВОЙСТВ ПРЯМОУГОЛЬНОГО ТЕТРАЭДРА

Автор работы:

Андреева Елена Валерьевна

ученица 11 «б» класса

Научный руководитель:

Солдаткина Клавдия Дмитриевна

Учитель математики

Город Кузнецк, 2004 год

ПЛАН.

І. Объект исследования.

ІІ. Цель исследования.

ІІІ. Доказательства свойств прямоугольного тетраэдра.

ІV. Практическое применение свойств прямоугольного тетраэдра.

V. Использованная литература.

І. ОБЪЕКТ ИССЛЕДОВАНИЯ

В работе впервые вводится понятие «Прямоугольный тетраэдр». Тетраэдр- многогранник, содержащий 4 грани. Тетраэдр является треугольной пирамидой и содержит 4 трёхгранных угла (рис. 1) Трёхгранный угол- фигура, образованная тремя плоскостями (гранями), имеющими общую точку (вершину) (рис 2) [1,2].

О О

А В

А В

С С

Рис. 1 Тетраэдр. Рис. 2 Трёхгранный угол.

Трёхгранный угол содержит три плоских угла, образованных рёбрами, лежащими на одной грани. Введем понятие прямого трехгранного угла. Назовем прямым трёхгранным углом трехгранный угол, содержащий три прямых плоских угла (рис3), т.е. рёбра трёхгранного угла взаимно перпендикулярны. Введем также понятие прямоугольного тетраэдра. Тетраэдр называется прямоугольным, если содержит прямой трёхгранный угол (рис 4).

А А

В В

О О

С

Рис. 3 Схема прямого Рис. 4 Схема прямоугольного

трёхгранного угла, тетраэдра.

Введем также понятия катетных граней, гипотенузной грани, катетов и гипотенуз прямоугольного тетраэдра. Прямоугольный тетраэдр содержит три катетные грани (грани, содержащие прямой плоский угол) и гипотенузную грань (не содержащую прямой угол). Прямоугольный тетраэдр содержит три катета (рёбра прямого трёхгранного угла) и три гипотенузы (рёбра, лежащие на гипотенузной грани). Тетраэдр, катеты которого равны, назовем равнокатет-ным.

ІІ. ЦЕЛЬ ИССЛЕДОВАНИЯ

Установление или доказательство свойств прямоугольного тетраэдра

Актуальность темы: прямоугольный тетраэдр является простейшей геометрической фигурой, обладающей уникальными свойствами. Изучение этих свойств в школьном курсе математики должно способствовать развитию абстрактного и логического мышления у учащихся.

ІІІ. ДОКАЗАТЕЛЬСТВА СВОЙСТВ ПРЯМОУГОЛЬНОГО ТЕТРАЭДРА.

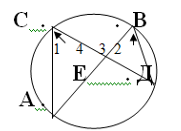
I. Квадрат площади гипотенузной грани равен сумме квадратов площадей катетных граней.

А

Дано:

ОАВС - прямоугольный тетраэдр

SОАВ= S1 SABC= S

SOBC= S2 SOAC= S3 В

Доказать: О

D

SІ=S1І+S2І+S3І

С

Доказательство.

Пусть AD- высота гипотенузной грани АВС, проведённая к ребру ВС из вершины А, ОD- проекция AD на катетной грани ОВС, OD перпендикулярно ВС, т.к. AD перпендикулярно ВС и АО перпендикулярно ОВС (обратная теорема о трёх перпендикулярах). SABC= 1/2 BCAD

SOBC=1/2 BCOD

SOAB =1/2 OAOB

SOAC=1/2OAOC

SІ OBC+S ІOAB +S ІAOC= 1/4(BCІODІ+OAІOBІ+OAІOCІ)=

=1/4(BCІODІ+OAІ(OBІ+OCІ))=1/4(BCІODІ+OAІBCІ), т.к.

ОВІ+ОСІ=ВСІ (по теореме Пифагора)

SІOBC+SІOAB+SІOAC=1/4 BCІ(ODІ+OAІ)=1/4 BCІADІ , т.к.

ODІ+OAІ=ADІ (по теореме Пифагора)

т.е. SІOBC+SІOAB+SІOAC=SІABC

SІ1+SІ2+SІ3=SІ, что и требовалось доказать.

II. Сумма квадратов гипотенуз равна удвоенной сумме квадратов катетов.

Дано: А

ОАВС- прямоугольный тетраэдр

где а , b , с - катеты. В

АВ, ВС и АС- гипотенузы а

Доказать: b

АВІ+ВСІ+АСІ=2(аІ + b І +сІ)

Доказательство. О

АВІ = аІ + b І с С ВСІ = b І + сІ (по теореме Пифагора)

АСІ = аІ + сІ

АВІ + ВСІ + АСІ =2аІ + 2 b І +2сІ , что и требовалось доказать.

III. Объём прямоугольного тетраэдра равен 1/6 произведения катетов.

А

Дано:

ОАВС - прямоугольный тетраэдр

а , b , с - катеты. В

Доказать: а b

V=(1/6) а · b · с

Доказательство. О С

с

Поскольку тетраэдр является треугольной пирамидой, его объём

V=(1/3 )Sосн · h

Выберем в качестве основания катетную грань ОВС, тогда катет а будет высотой тетраэдра, т.к. а перпендикулярен ОВС, т.е.

V=(1/3) SOBC· а , т.к.SOBC=(1/2) b ·.с

Имеем V=(1/6) а · b · с, что и требовалось доказать.

Расстояние от вершины прямого трёхгранного угла до гипотенузной грани определяется по формуле:

_______________

h = (a۰b۰c)/√aІ·bІ + bІ·cІ + aІ·cІ

где a, b, c – катеты тетраэдра

Дано: А ОАВС- прямоугольный тетраэдр

ОА = а, ОВ = b, ОС = с катеты Д

ОД = h – перпендикуляр к грани

АВС а

h В

Доказать:b

____________ О

h = (a·b·c) / √aІbІ+bІcІ+aІcІс С

Доказательство.

Объем тетраэдра:

V = (1/3)S_АВС·h

C другой стороны: V = (1/6)abc (свойство 3 прямоугольного тетраэдра).

Следовательно,

h = (abc) / (2S_АВС)

Из первого свойства прямоугольного тетраэдра:

___________________

S_АВС= √ЅІ_ОАВ + SІ_ОВС+SІ_ОАС

____________

т.е. S_АВС= (1/2)√aІbІ+bІcІ+aІcІ

Следовательно,

____________

h = (abc) / √aІbІ+bІcІ+aІcІ , что и требовалось доказать.

Косинусы направляющих углов нормали к гипотенузной грани определяются по формулам:

____________

cos α = h / a= (bc) / √aІbІ+bІcІ+aІcІ

____________

сos β = h / b = (ac) / √aІbІ+bІcІ+aІcІ

____________

cos γ = h / c= (ab) / √aІbІ+bІcІ+aІcІ

где a, b, c – катеты тетраэдра;

α – угол между катетом а и нормалью

β – угол между катетом b и нормалью

γ – угол между катетом с и нормалью.

h – нормаль

Дано:

ОАВС - прямоугольный тетраэдр.

ОА = а, ОВ = b, ОС = с - катеты

ОД = h – нормаль к грани АВС А

Доказать: Д ____________

cos α = (bc) / √aІbІ +bІcІ +aІcІh

____________ а В

cos β = (ac) / √aІbІ +bІcІ +aІcІαb

____________ β

cos γ = (ab) / √aІbІ +bІcІ +aІcІ γ

С

О с

Доказательство.

Соединим точку Д с точкой А и получим прямоугольный треугольник ОАД

cos α = ОД/ОА = h/a

____________

Поскольку h = (abc) / √aІbІ+bІcІ+aІcІ

____________

cos α = (bc)/√aІbІ+bІcІ+aІcІ , что и требовалось доказать.

Аналогично:

____________

cos β = ОД/ОВ = d/b = (ac)/√aІbІ+bІcІ+aІcІ

____________

cos γ = ОД/ОС = d/c = (ab)/√aІbІ+bІcІ+aІcІ

Радиус сферы, описывающей прямоугольный тетраэдр, определяется по формуле:

________

R = ( Ѕ) · √aІ+bІ+cІ

где a, b, c – катеты тетраэдра

К L

Дано:

ОАВС- прямоугольный тетраэдр А М

ОА = а, ОВ = b, ОС = с – катеты

R – радиус сферы, описывающей

тетраэдр.

Доказать: а

_______ В Д

R = (1/2)√aІ+bІ+cІb

О

Доказательство. с С

На базе прямоугольного тетраэдра

ОАВС достраиваем прямоугольный параллелепипед ОВДСАКЛМ. Диагонали прямоугольного параллелепипеда являются диаметрами описывающей его сферы, т.к. центр симметрии прямоугольного параллелепипеда совпадает с центром описанной сферы т.е.:

_______ _____ ________

КС = D = √aІ+bІ+cІ (ВС = √bІ+cІ , ВК = а, КС = √ВСІ+ВКІ )

Поскольку данная сфера одновременно описывает прямоугольный

тетраэдр, имеем:

_______

R = (1/2)D = (1/2)√aІ+bІ+cІ,

что и требовалось доказать.

VII. Радиус сферы, вписанной в прямоугольный тетраэдр, определяется по формуле:

abc

r = ____________ ,

√aІbІ+bІcІ+aІcІ + ab + bc + ac

где a, b, c - катеты тетраэдра.

Дано: ОАВС - прямоугольный тетраэдр

ОА = а, ОВ = b, ОС = с – катеты. О₁ – центр вписанной сферы

r - радиус вписанной сферы

Доказать:

r = h / (1 + cosα + cosβ + cosγ)

Доказательство: Пусть вписанная сфера касается гипотенузной грани в точке Д. Тогда О₁Д перпендикулярна гипотенузной грани и О₁Д = r.

_ _

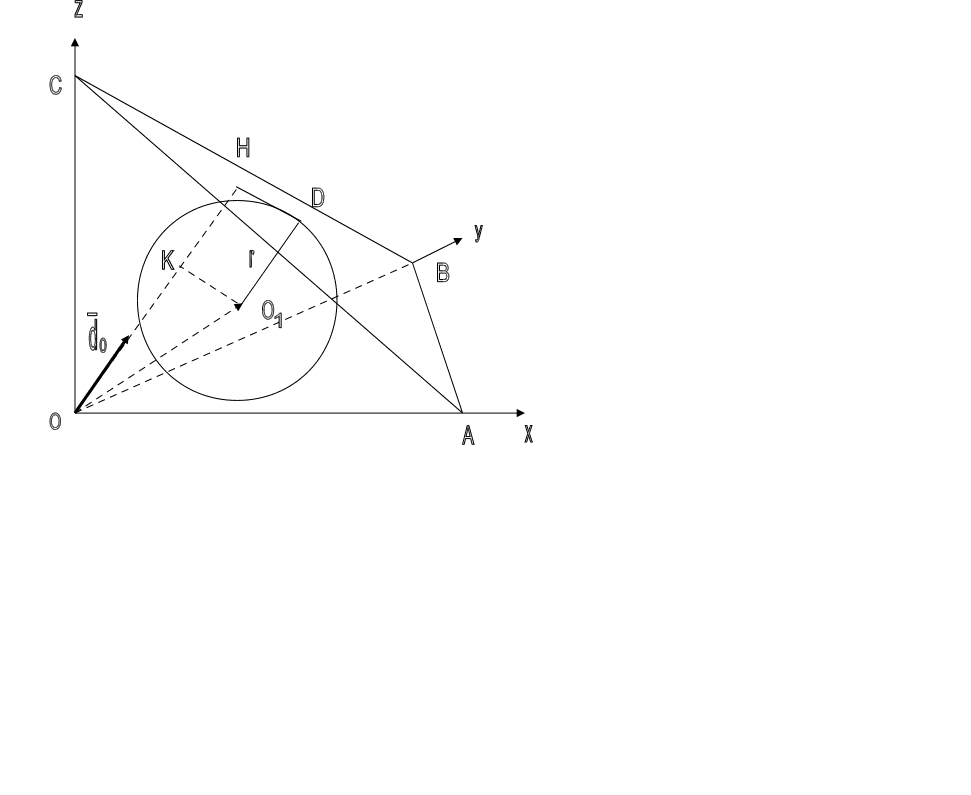
Пусть d_o - единичный вектор нормали к гипотенузной грани, т.е. |d_о| = 1

Координаты этого единичного вектора (cos α; cos β; cos γ) являются направляющими косинусами нормали к гипотенузной грани.

__

Найдем проекцию вектора ОО₁с координатами (r; r; r) на вектор нормали:

___ __

ОК = |ОО₁|cosδ , где δ – угол между вектором ОО₁и вектором нормали.

___ __ _ __ _

|OO₁|cosδ = (OO₁·d_o) = r·cosα + r·cosβ + r·cosγ , где (ОО₁·d_о) – скалярное произведение двух векторов.

Пусть перпендикуляр к гипотенузной грани ОН = h,

тогда h = OK + KH, т.е.

h = |OO₁|cosδ + r, т.к. КН = r

(поскольку КНДО₁является прямоугольником).

Имеем

h = r cosα + r cosβ + r cosγ + r

т.е.

r = h / (1 + cosα + cosβ + cosγ)

С учетом 4-го и 5-го свойств прямоугольного тетраэдра имеем полную формулу:

____________

(abc)/√ aІbІ+bІcІ+aІcІabc

r = ____________ = ____________ ,

1 + (bc + ac + ab) / √aІbІ+bІcІ+aІcІ √aІbІ+bІcІ+aІcІ + ab + bc + ac

Свойства равнокатетного прямоугольного тетраэдра.

А

Дано:

ОАВС -прямоугольный тетраэдр

ОА = ОВ = ОС = а – а

катеты В

Доказать, что гипотенузная а

грань является правильным

треугольником и косинусы О Д

двугранных углов между

гипотенузной гранью и катетными а

гранями равны С

___

√1/3

Доказательство.

Стороны гипотенузной грани находим по теореме Пифагора:

_________ __

АС = √ ОАІ +OCІ = √2 а

_________ __

АВ = √ ОАІ +OBІ = √2 а

_________ __

ВС = √ ОВІ + ОСІ = √2 а

т.е. треугольник АВС равносторонний или правильный, что и требовалось доказать.

Проведем отрезок АД перпендикулярно ВС. Отрезок ОД является проекцией отрезка АД на грань ОВС и поэтому ОД будет перпендикулярен ВС по теореме о трех перпендикулярах. Следовательно, угол ОДА является линейным углом двугранного угла между гранями ОВС и АВС

Поскольку АД является высотой правильного треугольника АВС:

_ _ _ ___

АД = (√3/2)АВ = (√3/2)√2 а = √3/2 а

ОД является высотой равнобедренного прямоугольного треугольника ОВС, опущенной с вершины прямого угла. Следовательно:

_

ОД = а/√2

Косинус двугранного угла: __

сos _ОДА = ОД/АД = 1/√3 , что и требовалось доказать.

Результаты исследования: исследования позволили установить свыше 8 важнейших свойств прямоугольного тетраэдра. Поскольку эти исследования проводились впервые, все полученные результаты обладают научной новизной.

Формула, устанавливающая связь между площадями граней прямоугольного тетраэдра, является аналогом теоремы Пифагора для трехмерных фигур и поэтому имеет большую теоретическую значимость.

ІV. ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ СВОЙСТВ ПРЯМОУГОЛЬНОГО ТЕТРАЭДРА

Результаты исследований можно использовать при решении задач на факультативных занятиях по темам «Пирамида» и «Прямоугольный параллелепипед» в средней школе. С использованием свойств прямоугольного тетраэдра можно найти более рациональные и упрощенные варианты решения задач по сравнению с традиционными методами.

Например: задача №96 (стр.131) учебного пособия: В.М.Клопский, З.А.Скопец, М.И.Ягодовский. Геометрия.-М.: Просвещение, 1979.

Основанием пирамиды служит прямоугольный треугольник с катетами а и b, высота пирамиды проходит через вершину прямого угла основания и равна Н. Найти площадь полной поверхности.

А

Дано:

ОАВС- пирамида,

основанием является прямоугольный H

треугольник ОВС с катетами а и b В

ОА = Н, высота.

Найти: b

S полн. О Д

а

С

1) Решение по традиционной схеме:

S полн. = S_АОС + S_АОВ + S_ВОС + S_АВС

S_АОС = (1/2)аН; S_АОВ = (1/2)bН; S_ВОС = (1/2)аb;

Найдем основание и высоту боковой грани АВС с помощью теоремы Пифагора:

______ ________

ВС = √ аІ +bІ ; АД = √ ОДІ +НІ , где ОД – проекция высоты АД на основание ВОС.

Поскольку ОД _ ВС, из подобия треугольников ВОС и ВОД имеем:

______

ОД/ b = а/ВС или ОД = (аb)/ВС = (аb)/ √ аІ +bІ

Следовательно, _______________ ________________________

АД = √ (аb)/( аІ +bІ) + НІ = √[(аb)І +(bH)І + (аH)І]/( аІ +bІ)

_________________

В результате получаем S_АВС= (1/2) √ (аb)І +(bH)І + (аH)І

_________________

Cледовательно, S полн.= (1/2) [√ (аb)І +(bH)І + (аH)І + аН + bН + аb]

2)Решение с использованием первого свойства прямоугольного тетраэдра:

S полн.= S_АОС + S_АОВ + S_ВОС + S_АВС

S_АОС = (1/2)аН; S_АОВ = (1/2)bН; S_ВОС = (1/2)аb;

___________________ _________________

S_АВС= √ S_АОС І + S_АОВІ + S_ВОС І = (1/2)√ (аb)І +(bH)І + (аH)І

_________________

Cледовательно, S полн.= (1/2)(√ (аb)І +(bH)І + (аH)І + аН + bН + аb)

Задача №280 (стр.76) учебного пособия: Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия.-М.: Просвещение, 1994.

Ребро куба равно а. Найти площадь сечения, проходящего через диагонали двух его граней

К L

Дано:

ОВДСАКLM - куб А М

ОА = а, ОВ = b, ОС = с – ребра

ΔАВС – сечение куба плоскостью, прохо-

дящей через диагонали смежных а

граней. В Д

Найти:а

S_АВС О

а С

1) Решение по традиционной схеме:

Найдем стороны сечения АВС с помощью теоремы Пифагора:

______ __

АС = АВ = ВС = √ аІ + аІ = √2 а

Площадь правильного треугольника АВС найдем по формуле:

_ _ _

S_АВС= (√3/4)(АС)² , т.е. S_АВС= (√3/4)(2а²) = (√3/2)а²

2)Решение с использованием первого свойства прямоугольного тетраэдра:

S_АОС = S_АОВ = S_ВОС = (1/2)а² (поскольку тетраэдр равнокатетный);

___________________

S_АВС= √ S_АОС І + S_АОВІ + S_ВОС І

_________ _

Cледовательно, S_АВС= (1/2) √ аІ + аІ + аІ = (√3/2)а²

V. Список использованной литературы:

М.Я.Выгодский. Справочник по элементарной математике. Изд. 6-е, Гостехиздат, М.-Л., 1952.

А.П.Киселев. Геометрия. Учебник для средней школы, ч.1 и 2.- М.: Учпедгиз 1951.

Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. Геометрия. Учебник для средней школы.-М.: Просвещение, 1994.