Навигация
Лекции по математической статистике
Введение
Истоками математической статистики (М.С.) является большой объем статистических данных и потребность после их специальной обработки сделать прогноз развития исходной ситуации.
Первый раздел М.С. – описательная статистика – предназначена для сбора, представления в удобном виде и описания исходных данных. Описательная статистика обрабатывает два вида данных: количественные и качественные.
К количественным относятся рост, вес и т.д. к качественным – тип темперамента, пол.
Описательная статистика позволяет описать, обобщить, свести к желаемому виду свойства массивов данных.
Второй раздел М.С. – теория статистического вывода – это формализованная система методов решения задач, сводящихся к попытке вывести свойства большого массива данных путем обследования его малой части.
Статистический вывод строится на описательной статистике и от частных свойств выборки данных мы переходим к частным свойствам совокупности.
Третий раздел М.С. - планирование и анализ эксперта. Разработана для обнаружения и анализа причинных связей между переменными.
Измерение, шкалы и статистика
Измерение – это приписывание чисел объектам в соответствии с определенными правилами. Числа – это удобные в обработке объекты, в которые мы преобразуем определенные свойства нашего восприятия.
Шкала наименований или номинальная шкала. Номинальное измерение сводится к разбиению совокупности объектов на классы в каждом из которых сосредоточены объекты, идентичные по какому-нибудь признаку или свойству, например, по национальности, по полу, по типу темперамента.
При данных измерениях каждому из классов присваивается число, но оно используется исключительно как название этого класса и никаких операций над этими числами производить не предполагается.
Порядковое измерение возможно только тогда, когда в квалифицируемых объектах можно различить разную степень признака и свойства, на основе которого производится квалификация (например, конкурс красоты «Умники и умницы»). В данном случае числа используют только одно свое свойство – способность упорядочиваться.
Интервальная шкала принимается тогда, когда можно определить не только количество, свойства или признака в объекте, но также зафиксировать равные различия между объектами, то есть можно ввести единицу измерения для свойства или признака (например, температура, возраст).
Числа при интервальных измерениях имеют свойство упорядоченности и однозначности. Равные разности чисел соответствуют равным разностям значений измеряемого свойства или признака объекта.
Шкала отношений отличается от интервальной только тем, что точка отсчета не произвольна, а указывает на полное отсутствие измеряемого свойства или признака объекта.
Переменные и их измерение
Переменные бывают дискретные и непрерывные. При измерениях, особенно непрерывных свойств или признаков, можно достигнуть только косвенного значения переменной, то есть приближенного к точному и степень этого приближения будет определяться чувствительностью измерения.
Чувствительность определяется минимальной единицей цифровой шкалы, имеющейся в нашем распоряжении.
Пределы для точного значения устанавливаются путем прибавления и вычитания половины чувствительности измерительного процесса.
Множество чисел записывается с использованием произвольной величины с индексом, который указывает порядковый номер величины в цепи данных (xi).
Обозначение S и его свойства
1. ![]()
2. ![]()
3. ![]()
4. ![]()
5. ![]()
Табулирование и представление данных
Перед анализом и интерпретацией данных их обобщают.
Обобщение – запись данных в виде таблицы. Самый элементарный этап.
Ранжирование – упорядочение переменных от максимального до минимального или наоборот. Такое упорядочивание называется несгруппированным рангом.
Распределение частот. Проранжированный список сворачивают, указывая все полученные измерения подряд, однократно, а в соседней графе указывают частоту, с которой встречается данная оценка
Распределение сгруппированных частот применяется при большом количестве оценок (100 и более). Оценки группируются по признакам и каждая такая группа называется разрядом оценок. В случае полного поглощения этими группами всех данных, мы говорим о распределении сгруппированных частот.
Построение распределения сгруппированных частот
| Оценки | Интервал | Подсчет | Частота |
| 90 95 51 112 | 110-114 | 1 | 1 |
| 66 78 109 62 | 105-109 | 111 | 3 |
| 106 70 89 91 | 100-104 | 11 | 2 |
| 84 47 58 93 | 95-99 | 1111 | 4 |
| 105 95 59 84 | 90-94 | 111 | 3 |
| 83 100 72 | 85-89 | 1 | 1 |
| 104 69 74 | 80-89 | 111111 | 6 |
| 82 44 75 | 75-79 | 1111 | 4 |
| 97 80 81 | 70-74 | 1111 | 4 |
| 97 75 71 | 65-69 | 111 | 3 |
| 59 75 68 | 60-64 | 1 | 1 |
| 55-59 | 111 | 3 | |
| 50-54 | 1 | 1 | |
| 45-49 | 1 | 1 | |
| 44-45 | 1 | 1 |
Предварительно образовывать не менее 12 и более 15. Меньше 12 искажает результат, более 15 затрудняет работу с таблицей.
1) Определяем размах – разницу между максимальной и минимальной оценкой (112-44=69)
2) Выбор интервала разряда: 69:12=5,75
Определяем с уменьшением до 5: 69:15=4,6
3) Определение границ раздела. Необходимо образовать достаточное количество разрядов, чтобы не потерять самую маленькую и самую большую оценки, поэтому табулирование начнем с величины кратной интервалу. Ближайшее кратное 5 ниже нижней оценки – это 40. И делим на разряды до тех пор, пока не будет охвачена самая высокая оценка. Если необходимо сравнить 2 и более выборки, их помещают в такую же таблицу.
Квантили
Квантили – это способ описать группу измерений. Квантиль – это общее понятие.
Квантиль – точка на числовой шкале, которая делит совокупность наблюдений на группы с соответствующими пропорциями в каждой из них.
Квартиль – делит наблюдения на 4 группы (Q)
Дециль – делит наблюдения на 10 групп (D)
Квинтель – делит наблюдения на 5 групп (К)
Процентиль – делит наблюдения на 100 групп (Р)
Определение процентелей
Процентель представляет собой точку, ниже которой лежит Р % - в оценок.
Вычисление процентеля
| Оценка | 38 | 37 | 36 | 35 | 34 | 33 | 32 | 31 | 30 | 28 | 29 | 27 | 26 | 25 | 24 |
| Частота | 1 | 1 | 3 | 5 | 9 | 8 | 17 | 23 | 24 | 18 | 10 | 3 | 1 | 0 | 2 |
| Накопленная частота | 125 | 124 | 123 | 120 | 115 | 106 | 98 | 81 | 58 | 16 | 34 | 6 | 3 | 2 |
Для определения 25 процентиля P25 (границы под которой расположены 25% всех выставленных оценок)
Общая формула:
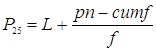
где:
n – общее число оценок
L – фактическая нижняя граница того раздела оценок, который включает себя нужную нам оценку
cumf – накопленная в данной нижней границе частота
f – количество оценок в данном разделе
p – определяемый процентиль (в данном случае 0,25)
p*n = 0,25*125=31,25
Находим фактическую нижнюю границу раздела L, содержащую 31,5 (это между 34 и 16).
Нижняя граница оценки 28,5
L=28,5 f=34-16=18
Вычитаем накопленную частоту L из произведения nf: ((31,25-16)/18) + 28,5=29,35
Для определения процентиля в случае наличия интервалов оценок, формула принимает вид:
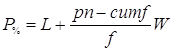
где W – ширина любого интервала оценок (в примере =1).
Наглядное представление данных
В табличных процессорах представляется возможность оформить численные данные в виде графика или диаграммы различного вида, но разновидностей графического представления данных существует больше, чем это предусмотрено программным обеспечением и прежде чем использовать какой-либо из видов необходимо:
· выделить в данных существенную информацию;
· знать все типы представления данных и сделать правильный выбор;
· знать и грамотно использовать потенциал аудитории, для представления которой готовятся данные;
· если оформление осуществляется не вами, разработать подробные и четкие инструкции для технического персонала с учетом имеющихся средств.
Примеры диаграмм и графиков: линейная, столбиковая, полосчатая, кумулятивная кривая, данные накапливаются с течением времени, пиктограмма – данные представляются в виде стилизованных изображений (улов рыбы в виде рыбы), логарифмическая диаграмма, круговая диаграмма.
Графическое представление распределения частот
1) Столбиковая диаграмма (гистограмма)
2) Полигон распределения
3) Сглаженная кривая
Гистограмма - это последовательность столбцов, каждый из которых опирается на один раздельный интервал, а высота столбца – это частота или количество случаев.
Принято распределять горизонтальную шкалу на один раздельный интервал вправо и влево от полученного диапазона. Чтобы гистограмма не получилась сплющенной или вытянутой, выбирают такой масштаб шкалы, чтобы ее ширина составляла 1 2/3 высоты. Середина столбца совмещается с срединой интервала, на практике ее изображают в форме контура, опуская вертикальные линии.
Полигон распределения – это та же гистограмма, но линии соединяют середины столбцов каждого разрядного интервала. Так как на разрядах справа и слева от разрядов распределения частот, частота имеет нулевое значение, поэтому полигон распределения продолжают до горизонтальной оси в середине интервала ниже меньшей оценки и выше высшей оценки.
Огива производится по точкам максимально приближенно без углов или острых фигур, ее называют кривой процентелей. Точки, определяющие кривую процентелей расположены по горизонтали у верхней границы каждого раздела. Огива проходит путь от 0 до 100%. При рисовании огивы надо следить за тем (особенно при малом числе объектов), чтобы, когда мы сглаживаем кривую, над ней оставались бы столько же точек, сколько и под ней. При отсутствии любых графических средств можно создать гистограмму на пишущей машинке в виде полосчатой диаграммы.
Гистограмма наиболее легка для восприятия и используется в тех случаях когда всего одно распределение. Если надо сравнить два и более распределений, используют полигон, чтобы избежать запутанной картины.
Огива дает возможность оценить квантили, медианы и другие характеристики точки. Удобно сравнивать несколько групп данных на одном графике.
Ошибки при использовании графиков
1) при создании графика не определяли положение нулевой точки;
2) представили значения в виде площадей в том случае, когда их надо было отражать линейно;
3) при использовании небольшого количества объектов сделали вывод относительно всей совокупности.
Правила графического оформления
1) Вся структура графика предполагает его чтение слева на право, вертикальные шкалы – снизу вверх;
2) На вертикальной шкале разместить нулевую отметку;
3) Если нулевая линия вертикальной шкалы не перпендикулярна по отношению к графику, то нулевая линия должна быть показана с помощью горизонтальной оси.
4) Пороговые точки на шкалах желательно выделить размером или цветом, но если речь идет о временном интервале, предпочтительно не указывать начальной и конечной точек. Подобрать такой масштаб, чтобы кривые линии резко отличались от прямых, желательно включить в график цифровые данные и изображение формулы, расположив их в правом верхнем углу, при необходимости использовать ясные полные заголовки и подзаголовки, как для самой диаграммы, так и для ее осей.
Меры центральной тенденции – первый момент, характеризующие данные
При исследовании массивов данных мы чаще всего оперируем величинами, характеризующими этот массив, именно по ним делаем вывод обо всей совокупности данных. К таким характеристикам относятся меры центральной тенденции, то есть значение наиболее часто встречающееся в данной совокупности. Этих мер существует несколько:
1) мода – это такое значение во множестве наблюдений которое встречается наиболее часто. Сложность в том, что редкая совокупность имеет единственную моду. (Например: 2, 6, 6, 8, 9, 9, 9, 10 – мода = 9).
Соглашения по поводу моры
· Если все значения в группе встречаются одинокого часто, считают, что у данной группы, моды нет.
· Когда два соседних значения имеют одинаковую частоту и эти частоты больше любых других частот в группе, то модой считают среднее от этих двух значений.
· Если два несмежных значения имеют равную и наибольшую в данной группе частоту, то у этой группы есть две моды, такая группа называется бимодальной. Бимодальной называется группа и в том случае, если эти две черты не совсем равны. В таких случаях договорились различать большую и малую моду и во всей группе, наряду с одной большой модой может быть несколько меньших мод.
2) медиана – это 50-тый процентиль в группе данных. 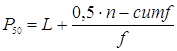
3) среднее (среднеарифметическое или выборочное среднее) – это сумма всех значений, разделенная на их количество. ![]() .
.
Мода наиболее просто вычисляется и при большом количестве измерений достаточно стабильна и близка к медиане и среднему. Медиана вычисляется по сложнее, особенно легко при ранжированных данных. В больших массивах предлагается сначала сгруппировать их, а потом вычислять медиану. Для определения моды и медианы не требуется знание всех остальных значений.
На определение среднего влияют значения всех изменений.
При наличии интервалов в значении, формула для среднего принимает вид:
![]()
1. Сумма всех n-отклонений от значения среднего должно быть равно нулю, то есть: ![]()
Похожие работы
... мышц и скоростью их сокращения, между спортивным достижением в одном и другом виде спорта и так далее. Теперь можно составить содержание элективного курса «Основы теории вероятностей и математической статистики» для классов оборонно-спортивного профиля. 1. Комбинаторика. Основные формулы комбинаторики: о перемножении шансов, о выборе с учетом порядка, перестановки с повторениями, размещения с ...
... опираться на теорию множеств, математическую логику, теорию алгоритмов. На основе применения «неколичественного» математического аппарата в теоретическом языкознании сформировалось направление, условно называемое комбинаторной лингвистикой – в ней используются методы математической статистики теории вероятностей, теории информации, математического анализа Современные инструментальные методы ...
... Доказать: По определению второй смешанной производной. Найдем по двумерной плотности одномерные плотности случайных величин X и Y. Т.к. полученное равенство верно для всех х, то подинтегральные выражение аналогично В математической теории вероятности вводится как базовая формула (1) ибо предлагается, что плотность вероятности как аналитическая функция может не существовать. Но т.к. в нашем ...
... гипотезу. Вроде бы это надо делать так: Теперь результаты наблюдений над выручкой G можно представить в виде четырех наблюдений над U: –11,+1,+3,+7. Теория математической статистики предлагает следующий, т.н. биномиальный критерий проверки гипотез в подобных ситуациях. Предполагается, что распределение вероятностей наблюдаемой величины U симметрично относительно значения математического ...







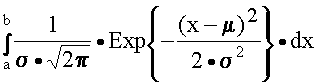
0 комментариев