Навигация
0 £ x £ 1
Пусть П играет в смешанных стратегиях, а В отвечает чистыми:
n1(х)= 2х-2(1-х) (1)
n2(х)= -2х+(1-х) (2)
n4(х)= -5х+3(1-х) (4)
n1(х)= 3х-2
n2(х)= -3х+1
n4(х)= -8х+3
т. В(х*, n*)
т. В: n1=n4
3х-2= -8х+3
11х=5
х*=5/11
n(х*)=×15/11-2= -7/11
р*(5/11; 1-5/11)=р*(5/11; 6/11) – оптимальная смешанная стратегия для П
Ищем оптимальную смешанную стратегию для В.
q(y, 0, 0, 1-y)
p1* = 5/11>0
Рассматриваем вариант, когда В играет в смешанных стратегиях, а П – в чистых стратегиях выбирает первую строку.
-7/11= 2y-5(1-y)
y*= 48/77
q*=(48/77, 0, 0, 29/77) – оптимальная смешанная стратегия В
Анализ модели краткосрочного страхования жизниВ страховой компании застраховано N1=900 человек в возрасте 45 лет и N2=550 человек в возрасте 55 лет сроком на один год. Компания выплачивает наследникам: 100000 руб., в случае смерти застрахованного от несчастного случая, и 25000 руб., в случае смерти от естественных причин в течение года. Компания не платит ничего, если человек проживет этот год. Предположим, что смертность описывается моделью Мейкхама и рассчитаем нетто-премию, цену полиса, страховую надбавку, чтобы вероятность неразорения компании составляла 0,95.
Индивидуальные иски x![]() и x
и x![]() каждого из застрахованных 1-ой и 2-ой групп определяются, соответственно, рядами распределения (для удобства за денежную единицу примем 100000 руб.).
каждого из застрахованных 1-ой и 2-ой групп определяются, соответственно, рядами распределения (для удобства за денежную единицу примем 100000 руб.).
0 ¼ 1 (1)
![]() x
x![]()
![]() =0,9982
=0,9982 ![]() =0,0013
=0,0013 ![]() =0,0005
=0,0005
![]()
![]()
![]() 0 ¼ 1
0 ¼ 1
![]() x
x![]()
![]() =0,9962
=0,9962 ![]() =0,0044
=0,0044 ![]() =0,0005
=0,0005
Здесь вероятности смерти от несчастного случая примем равными 0,0005, а вероятности смерти от естественных причин возьмем из Таблицы продолжительности жизни.
Средние индивидуальные иски Мx![]() и Мx
и Мx![]() равны соответствующим нетто-премиям Р
равны соответствующим нетто-премиям Р![]() и Р
и Р![]() для клиентов компании 1-ой и 2-ой групп.
для клиентов компании 1-ой и 2-ой групп.
Р![]() = Мx
= Мx![]() = ј*0,0013 + 1*0,0005 » 0,00083 = 83 руб. (2)
= ј*0,0013 + 1*0,0005 » 0,00083 = 83 руб. (2)
Р![]() = Мx
= Мx![]() = ј*0,0044 + 1*0,0005 » 0,0016 = 160 руб.
= ј*0,0044 + 1*0,0005 » 0,0016 = 160 руб.
I. Сначала рассмотрим решение, основанное на распределении Пуассона.
Чтобы свести задачу к схеме опытов Бернулли можно приближенно заменить ряды распределения (1) следующими таблицами:
![]()
![]()
![]()
![]() 0 М(x
0 М(x![]() /x
/x![]() №0) 0 М(x
№0) 0 М(x![]() /x
/x![]() №0)
№0)
![]()
![]() x
x![]() : x
: x![]() : (3)
: (3)
![]()
![]()
![]()
![]()
а затем в качестве условной денежной единицы принять условные математические ожидания М(x![]() /x
/x![]() №0) в 1-ой таблице и М(x
№0) в 1-ой таблице и М(x![]() /x
/x![]() №0) – во 2-ой.
№0) – во 2-ой.
Вычислим условные математические ожидания:
М(x![]() /x
/x![]() №0)=ј*Р(x
№0)=ј*Р(x![]() =ј/x
=ј/x![]() №0)+1*Р(x
№0)+1*Р(x![]() =1/x
=1/x![]() №0) = =ј*
№0) = =ј*![]() /(
/(![]() )+1*
)+1*![]() = =ј*0,0044/(0,0044+0,0005)+1*0,0005/(0,0044+0,0005)=
= =ј*0,0044/(0,0044+0,0005)+1*0,0005/(0,0044+0,0005)=
=ј*13/18+1*5/49 = 5/18 » 0,458=45800 руб. – денежная единица для клиентов 1-ой группы.
М(x![]() /x
/x![]() №0=ј*
№0=ј*![]() /(
/(![]() )+1*
)+1*![]() =
=
=ј*0,0044/(0,0044+0,0005)+1*0,0005/(0,0044+0,0005)=
=. ј*44/49+1*5/49 = 16/49 » 0,327=32700 руб – денежная единица для клиентов 2-ой группы.
С учетом всех замечаний вместо рядов распределения (3) имеем:
![]()
![]()
![]()
![]() 0 1 0 1
0 1 0 1
![]()
![]() x
x![]() : x
: x![]() : (4)
: (4)
0,9982 0,0018 0,9962 0,0049
откуда получаем: Мx![]() = 0,0018
= 0,0018
Мx![]() = 0,0049.
= 0,0049.
Подсчитаем сумму исков от застрахованных
1-ой группы:
l![]() =
= ![]() Мx
Мx![]() = N1* Мx
= N1* Мx![]() = 400*0,0018 = 0,7
= 400*0,0018 = 0,7
2-ой группы:
l![]() =
= ![]() Мx
Мx![]() = N2* Мx
= N2* Мx![]() = 1000*0,0049 = 4,9
= 1000*0,0049 = 4,9
Общая сумма исков может рассматриваться, как случайная пуассоновская величина с параметром l![]() +l
+l![]() = 5,6
= 5,6
Так как вероятность не разорения компании должна быть не меньше 0,95, необходимо чтобы для общей суммы исков от застрахованных
x = ![]() x
x![]() +
+ ![]() x
x![]()
выполнялось соотношение: Р(x Ј x) і 0,95 , где х – капитал компании.
Очевидно, что х = х![]() , здесь х
, здесь х![]() » 10– квантиль уровня 0,95 для распределения Пуассона. За счет нетто-премий компания может получить только сумму:
» 10– квантиль уровня 0,95 для распределения Пуассона. За счет нетто-премий компания может получить только сумму:
5,6=0,7*45800 руб. + 4,9*32700 руб. = 32060 руб.+1060230 руб. = 192290руб.
Поэтому страховая надбавка компании должна составлять:
R=(10-5,6)/5,6 ×100% »78,6% = 0,786*192290 руб.»1511400руб., (5)
а капитал компании:
х = 192290 руб. + 151140 руб. » 343430 руб. (6)
Таким образом, индивидуальные страховые надбавки r![]() и r
и r![]() , цены полисов Р
, цены полисов Р![]() и Р
и Р![]() для каждого из клиентов 1-ой и 2-ой группы соответственно равны (они пропорциональны нетто-премиям):
для каждого из клиентов 1-ой и 2-ой группы соответственно равны (они пропорциональны нетто-премиям):
r![]() = 0,52*Р
= 0,52*Р![]() = 0,52*83 руб. » 43 руб.,
= 0,52*83 руб. » 43 руб.,
r![]() = 0,52*Р
= 0,52*Р![]() = 0,52*160 руб. » 83 руб.,
= 0,52*160 руб. » 83 руб.,
(7)
Р![]() = Р
= Р![]() + r
+ r![]() » 43 руб. + 83 руб. = 126 руб.,
» 43 руб. + 83 руб. = 126 руб.,
Р![]() = Р
= Р![]() + r
+ r![]() »160 руб. + 83 руб. = 243 руб.
»160 руб. + 83 руб. = 243 руб.
II. Теперь решим задачу с помощью гауссовского приближения. Среднее значение общего суммарного иска от застрахованных
x = ![]() Мx
Мx![]() +
+ ![]() Мx
Мx![]()
с учетом средних индивидуальных исков (2) равно:
Мx = N1*Mx![]() + N2* Мx
+ N2* Мx![]() =400*0,00083+1000*0,0016=
=400*0,00083+1000*0,0016=
= 0,332 + 1,6 » 1,9 = 190000 руб. (8)
Дисперсию x в виду независимости x![]() и x
и x![]() вычислим по формуле:
вычислим по формуле:
Dx = ![]() Dx
Dx![]() +
+ ![]() Dx
Dx![]() » 400*0,00058 + 1000*0,00078=
» 400*0,00058 + 1000*0,00078=
=0,23 + 0,78 = 1,01. (9)
Здесь:
Dx![]() = М(x
= М(x![]() )
)![]() - М
- М![]() x
x![]() = 0,00058 – (0,00083)
= 0,00058 – (0,00083)![]() » 0,00058 ,
» 0,00058 ,
(10)
Dx![]() = М(x
= М(x![]() )
)![]() - М
- М![]() x
x![]() = 0,00078 – (0,0016)
= 0,00078 – (0,0016) ![]() » 0,00078 ,
» 0,00078 ,
где с помощью рядов распределения (1) имеем:
М(x![]() )
)![]() = 1/16*0,0013 + 1*0,0005 » 0,00058 ,
= 1/16*0,0013 + 1*0,0005 » 0,00058 ,
(11)
М(x![]() )
)![]() = 1/16*0,0044 +1*0,0005 » 0,00078.
= 1/16*0,0044 +1*0,0005 » 0,00078.
На основании центральной предельной теоремы функция распределения нормированной случайной величины:
![]() S
S![]() = (x - Mx)/
= (x - Mx)/![]() ,
,
при N1 + N2 ® Ґ имеет предел
F(x) = (1/![]() )*
)*![]() dz
dz
Для гауссовского приближения случайной величины x верна следующая цепочка равенств:
Р(x < x) = Р((x - Мx)/![]() Ј (х - Мx)/
Ј (х - Мx)/![]() ) » F((x - Mx)/
) » F((x - Mx)/![]() ) ,
) ,
где х – капитал компании.
Для того чтобы вероятность неразорения компании не превосходила 0,95, т.е.
F((x - Mx)/![]() ) і 0,95 должно быть выполнено соотношение
) і 0,95 должно быть выполнено соотношение
(х - Mx)/![]() і х
і х![]() , (12)
, (12)
здесь х![]() » 1,645 – квантиль уровня 0,95 стандартного гауссовского распределения.
» 1,645 – квантиль уровня 0,95 стандартного гауссовского распределения.
Нетрудно убедиться в том, что минимально необходимый капитал компании должен составлять:
х=Мx+х![]() *
*![]() »1,9+1,645*1,005=1,9+1,65=3,55=355000руб., (13)
»1,9+1,645*1,005=1,9+1,65=3,55=355000руб., (13)
а относительная страховая надбавка составляет:
х![]() *
*![]() /Мx*100%=1,65/1,9*100%»86,8% (14)
/Мx*100%=1,65/1,9*100%»86,8% (14)
Индивидуальные страховые надбавки r![]() и r
и r![]() , цены полисов Р
, цены полисов Р![]() и Р
и Р![]() для клиентов 1-ой и 2-ой групп с учетом (2), очевидно будут равны (страховые надбавки пропорциональны нетто-премиям):
для клиентов 1-ой и 2-ой групп с учетом (2), очевидно будут равны (страховые надбавки пропорциональны нетто-премиям):
r![]() = 0,68*83 руб. » 56 руб.;
= 0,68*83 руб. » 56 руб.;
r![]() = 0,68*160 руб. » 109 руб.;
= 0,68*160 руб. » 109 руб.;
(15)
Р![]() = Р
= Р![]() + r
+ r![]() »83 руб. + 56 руб. = 139 руб.;
»83 руб. + 56 руб. = 139 руб.;
Р![]() = Р
= Р![]() + r
+ r![]() »160 руб. + 109 руб. = 269 руб.
»160 руб. + 109 руб. = 269 руб.
III. Проанализируем результаты, полученные в п.п. I и II. Очевидно расхождение результатов, полученных при использовании пуассоновского и гауссовского приближений. Попытаемся разобраться, в чем причина этого различия.
Дело в том, что при использовании закона Пуассона замена рядов распределения (1) на ряды распределения (3) привела к тому, что не изменились лишь математические ожидания Мx![]() и Мx
и Мx![]() . В то же время дисперсии Dx
. В то же время дисперсии Dx![]() и Dx
и Dx![]() , свидетельствующие о степени рассеяния случайных исков x
, свидетельствующие о степени рассеяния случайных исков x![]() и x
и x![]() , найденных по рядам распределения (1) и (3), различны. Следовательно, различны и дисперсии Dx, найденные по рядам распределения (1) и (3). Действительно, дисперсия общего суммарного иска x по рядам (1) подсчитана: Dx = 1,24 (см. соотношение (9) ).
, найденных по рядам распределения (1) и (3), различны. Следовательно, различны и дисперсии Dx, найденные по рядам распределения (1) и (3). Действительно, дисперсия общего суммарного иска x по рядам (1) подсчитана: Dx = 1,24 (см. соотношение (9) ).
Вычислим дисперсию x по рядам распределения (3), т.е.
![]()
![]()
![]()
![]() 0 0,458 0 0,327
0 0,458 0 0,327
![]()
![]() x
x![]() : x
: x![]() : (16)
: (16)
0,9982 0,0018 0,9962 0,0049
Проведя расчеты, аналогичные (9-11), получим:
Dx =![]() Dx
Dx![]() +
+ ![]() Dx
Dx![]() » 400*0,00038 + 1000*0,00052 = 0,67. (17)
» 400*0,00038 + 1000*0,00052 = 0,67. (17)
Здесь:
Dx![]() = М(x
= М(x![]() )
)![]() - М
- М![]() x
x![]() = 0,00038 – (0,00083)
= 0,00038 – (0,00083)![]() » 0,00038 ,
» 0,00038 ,
(18)
Dx![]() = М(x
= М(x![]() )
)![]() - М
- М![]() x
x![]() = 0,00052 – (0,0016)
= 0,00052 – (0,0016) ![]() » 0,00052 ,
» 0,00052 ,
причем:
М(x![]() )
)![]() = 0,458
= 0,458![]() *0,0018 » 0,00038 ,
*0,0018 » 0,00038 ,
(19)
М(x![]() )
)![]() = 0,327
= 0,327![]() *0,0049 » 0,00052.
*0,0049 » 0,00052.
В дальнейшем будем использовать следующие обозначения: дисперсию x, найденную с использованием рядов (1), обозначим s![]() , а дисперсию x, найденную по рядам (3) или (16), обозначим s
, а дисперсию x, найденную по рядам (3) или (16), обозначим s![]() . Таким образом, s
. Таким образом, s![]() = 1,01, а s
= 1,01, а s![]() = 0,67.
= 0,67.
Из формулы (12), использующей стандартное гауссовское распределение, непосредственно следует, что относительная страховая надбавка, если Dx = s![]() = 0,67 , равна
= 0,67 , равна
х![]() *s
*s![]() /Мx*100% = 1,645*
/Мx*100% = 1,645*![]() /1,9*100% » 70,9% (20)
/1,9*100% » 70,9% (20)
Этот результат хорошо согласуется с относительной страховой надбавкой, учитывающей распределение суммарного иска x по закону Пуассона, равной 86,8% (см. (5)).
Учитывая вышеизложенное, напрашивается естественный вывод: если относительная страховая надбавка, капиталл компании, обеспечивающий неразорение компании с вероятностью 0,95, и цена полиса вычисляются, исходя из распределения суммарного иска застрахованных по закону Пуассона, то для нахождения основных характеристик компании необходимо ввести поправочный коэффициент, равный k = s1 /s2.
Проиллюстрируем применение коэффициента k для коррекции результатов, полученных в п.I:
страховая надбавка с учетом (5) станет равной:
R![]() = k*R =
= k*R = ![]() *86,8%=1,2*86,8% » 71,4% » 135660 руб. (21)
*86,8%=1,2*86,8% » 71,4% » 135660 руб. (21)
капитал компании (см.(6)) станет равным:
х![]() = 190000 руб. + 135660 руб. » 325660 руб., (22)
= 190000 руб. + 135660 руб. » 325660 руб., (22)
а индивидуальные страховые надбавки и цены полисов (см.(7)):
r![]()
![]() = k*r
= k*r![]() » 1,2*43 руб. » 54 руб.,
» 1,2*43 руб. » 54 руб.,
r![]()
![]() = k*r
= k*r![]() » 1,2*83 руб. » 100 руб.,
» 1,2*83 руб. » 100 руб.,
(23)
Р![]()
![]() = Р
= Р![]() + r
+ r![]()
![]() » 83 руб. + 54 руб. = 137 руб.,
» 83 руб. + 54 руб. = 137 руб.,
Р![]()
![]() = Р
= Р![]() + r
+ r![]()
![]() » 160 руб. + 100 руб. = 260 руб.
» 160 руб. + 100 руб. = 260 руб.
В заключение необходимо отметить, что характеристики работы компании, полученные с учетом коррекции результатов исследования, в котором суммарный иск застрахованных подчинен распределению Пуассона хорошо согласуется с характеристиками работы страховой компании.
Похожие работы
... решаются точно так же, как задачи с аддитивным критерием, с той единственной разницей, что в основном уравнении (1.2) вместо знака «плюс» ставится знак «умножения»: 1.2 Примеры задач динамического программирования Задача планирования рабочей силы: При выполнении некоторых проектов число рабочих, необходимых для выполнения какого-либо проекта, регулируется путем их найма и увольнения. ...
... := f(n, Yk, j, H,P,C, Wt); if Result < ft then begin Result := ft; W := Wt; W[j].E := true; W[j].N := n; end; end; end; end. 2. Метод ветвей и границ 2.1 Теоретическая часть Рассмотрим следующую задачу целочисленного программирования. Требуется максимизировать выражение: n L=∑cj∙xj(4) j=1 при ограничениях n ∑аij∙xj≤bi, i=1, …,m ...
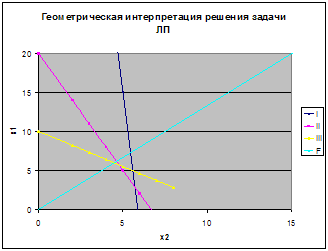
... разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями. Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах ...
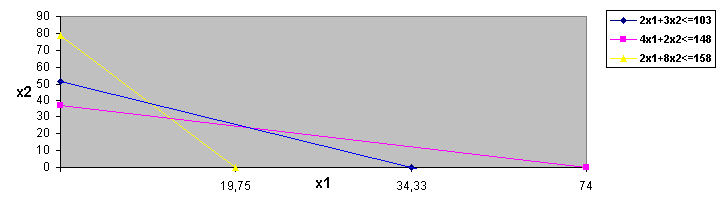
... а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке. Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок у(у1, y2, y3) минимизирующий общую оценку всех ресурсов f = 103у1 + 148у2 + 158у3 (1) при условии, что по каждому виду ...
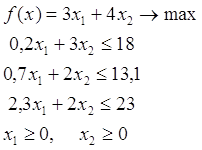
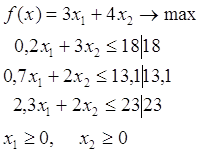
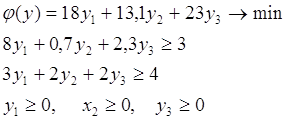
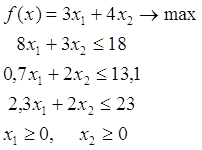
0 комментариев