Министерство науки, высшей школы и технической политики Российской Федерации.
Новосибирский Государственный
Технический Университет.

Контрольная работа по специальным главам математики.
Факультет: АВТ.
Кафедра: АСУ.
Группа: А-513.
Студент: Бойко Константин Анатольевич.
Преподаватель: Хоменко Валентин Михайлович.
Дата: 5 мая 1997 года.
Новосибирск
Исходные данные.| 0 | 2 | 4 | 6 | 8 | 10 | 12 | |
| X1 | 1,4 | -1,7 | 5,3 | -2,5 | 2,2 | 3,1 | -1,9 |
| X2 | 0 | 4,5 | 4,2 | 0,7 | -2,3 | -1,4 | 1,9 |
| X3 | -7,5 | 9,2 | -2,1 | 6,9 | -3,1 | -1,7 | -0,8 |
| X4 | 2,0 | 1,3 | 8,4 | 4,2 | -2,6 | 2,8 | 6,2 |
| X5 | -2,0 | 3,1 | 6,4 | 8,2 | 7,3 | 2,5 | -3,0 |
| X6 | 0 | -0,9 | 1,0 | 0,2 | -0,9 | 1,0 | -0,3 |
| X7 | 3,8 | -3,1 | -3,6 | 2,0 | 4,3 | 2,7 | -0,8 |
| X8 | -4,7 | -1,2 | 1,7 | 2,9 | 1,0 | -1,9 | -4,6 |
| X9 | 1,4 | 6,1 | 2,2 | 5,8 | -4,5 | 5,3 | 8,3 |
| X10 | -2,6 | -2,4 | -0,7 | -0,9 | -2,4 | -3,4 | -1,9 |
| X11 | 0 | 2,3 | 3,7 | 4,0 | 2,0 | 1,1 | 0,6 |
| X12 | -2,2 | -1,7 | -3,5 | -5,5 | -6,3 | -4,1 | 0,7 |
| X13 | -5,2 | -7,4 | -5,2 | -3,2 | -4,0 | -4,9 | -3,3 |
| X14 | 6,0 | 1,9 | 2,0 | 6,8 | 4,7 | 2,5 | 3,9 |
1. Построим матрицу mxt(t).
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| mxt | -0,686 | 0,714 | 1,414 | 2,114 | -0,329 | 0,257 | 0,357 |
2. Строим корреляционную матрицу.
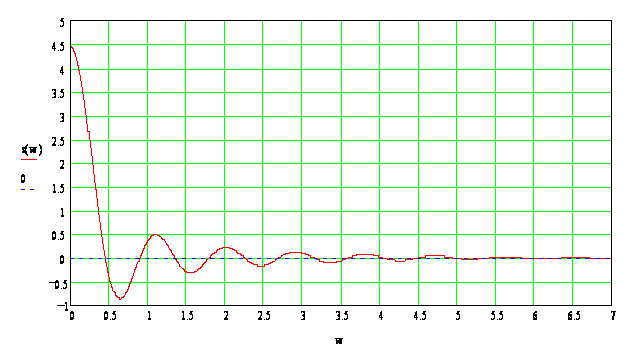
![]() ,
,
…
![]() ;
;
![]() ,
,
…
![]() ;
;
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| 0 | 12,339 | -0,419 | 5,051 | 2,216 | 5,558 | 7,507 | 7,095 |
| 2 | -0,419 | 16,666 | 6,232 | 11,676 | -0,117 | 4,688 | 6,792 |
| 4 | 5,051 | 6,232 | 14,917 | 6,909 | 5,475 | 7,111 | 4,606 |
| 6 | 2,216 | 11,676 | 6,909 | 12,861 | 7,498 | 6,980 | 4,422 |
| 8 | 5,558 | -0,117 | 5,475 | 7,498 | 14,741 | 5,712 | -3,907 |
| 10 | 7,507 | 4,688 | 7,111 | 6,980 | 5,712 | 9,104 | 6,028 |
| 12 | 7,095 | 6,792 | 4,606 | 4,422 | -3,907 | 6,028 | 12,490 |
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| Dx | 12,339 | 16,666 | 14,917 | 12,861 | 14,741 | 9,104 | 12,490 |
| dx | 3,513 | 4,082 | 3,862 | 3,586 | 3,839 | 3,017 | 3,534 |
3. Строим нормированную корреляционную матрицу.
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| 0 | 1 | -0,029 | 0,372 | 0,176 | 0,412 | 0,708 | 0,571 |
| 2 | -0,029 | 1 | 0,395 | 0,798 | -0,007 | 0,381 | 0,471 |
| 4 | 0,372 | 0,395 | 1 | 0,499 | 0,369 | 0,610 | 0,337 |
| 6 | 0,176 | 0,798 | 0,499 | 1 | 0,545 | 0,645 | 0,349 |
| 8 | 0,412 | -0,007 | 0,369 | 0,545 | 1 | 0,493 | -0,288 |
| 10 | 0,708 | 0,381 | 0,610 | 0,645 | 0,493 | 1 | 0,565 |
| 12 | 0,571 | 0,471 | 0,337 | 0,349 | -0,288 | 0,565 | 1 |
![]() , … ,
, … , ![]() .
.
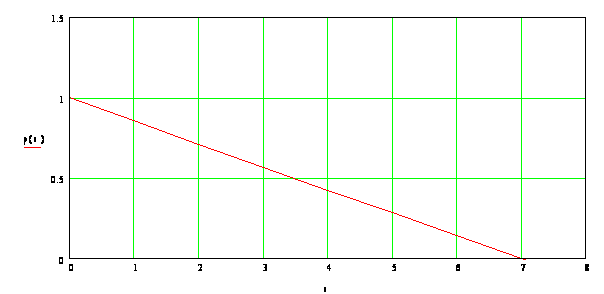
4. Строим таблицу r(t).
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| r | 1 | 0,411 | 0,379 | 0,282 | 0,377 | 0,590 | 0,571 |
Строим график нормированной корреляционной функции (при необходимости аппроксимируем по методу наименьших квадратов).
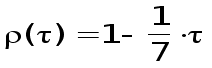
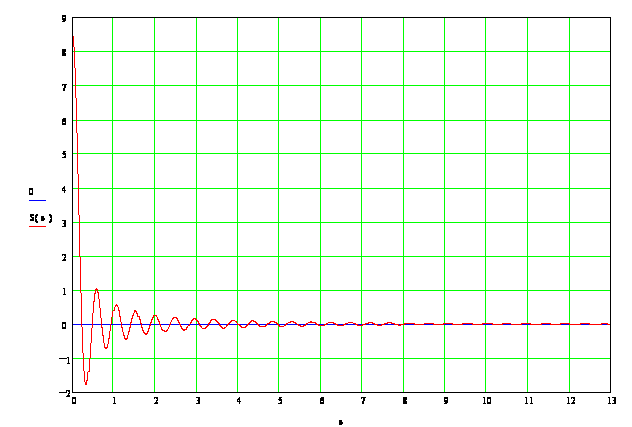
5. Найдем спектральную характеристику Sx(w) и построим её график.
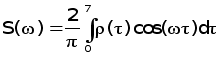
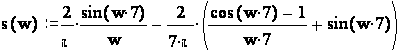
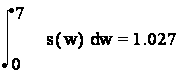
Министерство науки, высшей школы и технической политики Российской Федерации.
Новосибирский Государственный
Технический Университет.

Контрольная работа по специальным главам математики.
Факультет: АВТ.
Кафедра: АСУ.
Группа: А-513.
Студент: Борзов Андрей Николаевич.
Преподаватель: Хоменко Валентин Михайлович.
Дата: 10 мая 1997 года.
Новосибирск – 1997.

| 0 | 2 | 4 | 6 | 8 | 10 | 12 | |
| X1 | -10 | 8.391 | -4.081 | -1.543 | 6.669 | -9.65 | 9.524 |
| X2 | 3.536 | 0.365 | -4.012 | 4.881 | -2.368 | -1.785 | 4.701 |
| X3 | 0.721 | 0.229 | 0.721 | 0.114 | 6.835 | 0.244 | 0.252 |
| X4 | 2.718 | 1.94 | 0.885 | 0.439 | 0.379 | 0.631 | 1.432 |
| X5 | 0 | 3.934 | -2.402 | -5.716 | -1.382 | -6.299 | -3.36 |
| X6 | 0.667 | -0.099 | -0.465 | 0 | 0.635 | 0.331 | -0.445 |
| X7 | 8.999 | 6.524 | 1.183 | 7.583 | 1.021 | 7.315 | 1.011 |
| X8 | -7.568 | -0.484 | 4.227 | -5.015 | -0.114 | 6.974 | -2.05 |
| X9 | -0.661 | 4.998 | -1.017 | 1.683 | 4.545 | -3.739 | 3.496 |
| X10 | 0 | -0.497 | -0.8 | 0.247 | -0.008 | -0.397 | 0.333 |
| X11 | 1 | 0.336 | 0.931 | 0 | 0.143 | 0.314 | 0 |
| X12 | -4.741 | 2.22 | 0.01 | -4.854 | 0.02 | 0.006 | -4.55 |
| X13 | 0 | -2.961 | -3.872 | -1.701 | -2.786 | -0.085 | -5.197 |
| X14 | 0 | 0.328 | 1.339 | 2.677 | 4.247 | 6.001 | 7.907 |
1. Построим матрицу mxt(t).
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| mxt | -0.38 | 1.8 | -0.525 | -0.086 | 1.274 | -0.01 | 0.932 |
2. Строим корреляционную матрицу.
![]() ,
,
…
![]() ;
;
![]() ,
,
…
![]() ;
;
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| 0 | 20.072 | -1.34 | 0.655 | 11.543 | -3.915 | 7.718 | -1.858 |
| 2 | -1.34 | 9.03 | -1.198 | 1.766 | 4.212 | -5.479 | 5.756 |
| 4 | 0.655 | -1.198 | 5.341 | -0.267 | 0.904 | 8.101 | -1.556 |
| 6 | 11.543 | 1.766 | -0.267 | 12.725 | 1.464 | 6.552 | 7.517 |
| 8 | -3.915 | 4.212 | 0.904 | 1.464 | 8.862 | -2.406 | 7.679 |
| 10 | 7.718 | -5.479 | 8.101 | 6.552 | -2.406 | 20.64 | -3.602 |
| 12 | -1.858 | 5.756 | -1.556 | 7.517 | 7.679 | -3.602 | 17.288 |
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| Dx | 20.072 | 9.03 | 5.341 | 12.725 | 8.862 | 20.64 | 17.288 |
| dx | 4.48 | 3.005 | 2.311 | 3.567 | 2.977 | 4.543 | 4.158 |
3. Строим нормированную корреляционную матрицу.
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
| 0 | 1 | -0.1 | 0.063 | 0.722 | -0.294 | 0.379 | -0.1 |
| 2 | -0.1 | 1 | -0.173 | 0.165 | 0.471 | -0.395 | 0.461 |
| 4 | 0.063 | -0.173 | 1 | -0.032 | 0.131 | 0.772 | -0.162 |
| 6 | 0.722 | 0.165 | -0.032 | 1 | 0.138 | 0.404 | 0.507 |
| 8 | -0.294 | 0.471 | 0.131 | 0.138 | 1 | -0.178 | 0.62 |
| 10 | 0.379 | -0.395 | 0.772 | 0.404 | -0.178 | 1 | -0.19 |
| 12 | -0.1 | 0.461 | -0.162 | 0.507 | 0.62 | -0.19 | 1 |
![]() , … ,
, … , ![]() .
.
4. Строим таблицу r(t).
| t | 0 | 2 | 4 | 6 | 8 | 10 | 12 |
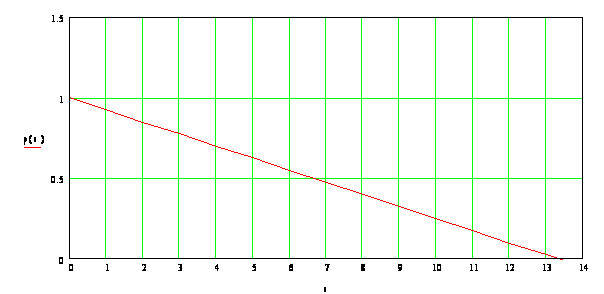
| r | 1 | -0.089 | 0.277 | 0.618 | -0.284 | 0.42 | -0.1 |
Строим график нормированной корреляционной функции (при необходимости аппроксимируем по методу наименьших квадратов).
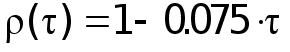

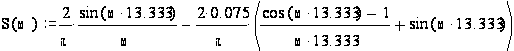
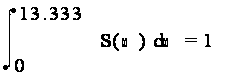
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
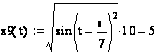
![]()
![]()
![]()
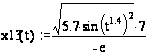
![]()
Похожие работы
... факт; доказательство получается с помощью обратной процедуры.) Принято считать, что последователи Платона изобрели метод доказательства, получивший название «доказательство от противного». Заметное место в истории математики занимает Аристотель, ученик Платона. Аристотель заложил основы науки логики и высказал ряд идей относительно определений, аксиом, бесконечности и возможности геометрических ...
... неравенство |xi|/t>=1. Учитывая это неравенство получаем: P{|X|>=t}=сумма по i: |xi|>=t pi <=сумма по i:|xi|>=t |xi|/t pi<=сумма по i:|xi|>=t |xi|/t pi+сумма по i:|xi|<t |xi|/t*pi =1/t сумма по i от 1 до бесконечности |xi|*pi=1/t*M|X|. 2) Для Н.С.В. Х. Пусть Х – Н.С.В. с плотностью вероятности р(х). Вероятность того, что |X|>=t, равна сумме интегралов от плотности ...
... ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x) y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x) sin(x)=t Билет №22 Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида : где P(x) и Q(x) – непрерывные функции m – ...
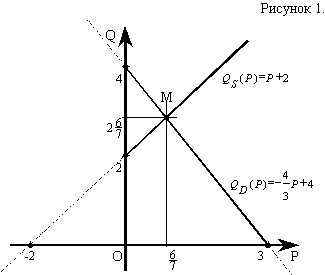
ние месяца, не выходящих в рейс из-за профилактического ремонта автомашин. дней в месяц каждый водитель из штата гаража не выходит в рейс из-за профилактического ремонта автомашин. Ответ:Каждый водитель из штата гаража в течение месяца может иметь свободных дней. Задание №3. Вопрос №1. Построить график функции спроса Q=QD(P) и предложения Q=QS(P) и найдите координаты точки равновесия, если , ...
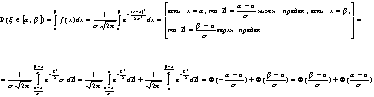
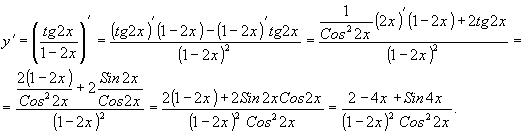
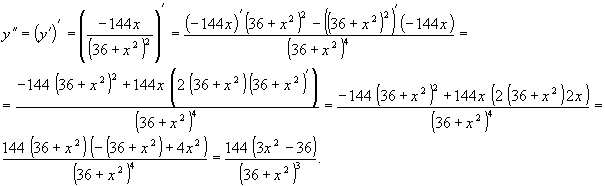
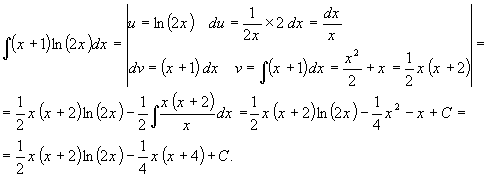
0 комментариев