*1. Говорят, что функция f(x) не убывает (не возрастает) на (a,b), если для любых точек x1<x2 из (a,b) справедливо неравенство f(x1)£f(x2) (f(x1)³f(x2)).
*2. Говорят, что функция f(x) возрастает (убывает) на (a,b), если x1<x2 из (a,b) справедливо неравенство f(x1)<f(x2) (f(x1)>f(x2)). В этом случае функцию называют монотонной на (a,b).
Т1. Дифференцируемая на (a,b) функция f(x) тогда и только тогда не убывает (не возрастает) на (a,b), когда f¢(x)³0 (£0) при любом xÎ(a,b).
Док-во: 1) Достаточность. Пусть f¢(x)³0 (£0) всюду на (a,b). Рассмотрим любые x1<x2 из (a,b). Функция f(x) дифференцируема (и непрерывна) на [x1,x2]. По теореме Лагранжа: f(x2)-f(x1)=(x2-x1)f¢(a), x1<a<x2. Т.к. (x2-x1)>0, f¢(a)³0 (£0), f(x2)-f(x1)³0 (£0), значит, f(x) не убывает (не возрастает) на (a,b). 2) Необходимость. Пусть, например, f(x) не убывает на (a,b), xÎ(a,b), x+DxÎ(a,b), Dx>0. Тогда (f(x+Dx)-f(x))/Dx³0. Переходя к приделу при Dxà0, получим f¢(x)³0. Теорема доказана.
Т2. Для возрастания (убывания) f(x) на (a,b) достаточно, чтобы f¢(x)>0 (<0) при любом xÎ(a,b). Док-во: Тоже что и в Т2.
Замечание1. Обратное к теореме 2 не имеет места, т.е. если f(x) возрастает (убывает) на (a,b), то не всегда f¢(x)>0 (<0) при любом xÎ(a,b).
*3. Прямая х=а называется вертикальной асимптотой графика функций y=f(x), если хотя бы одно из предельных значений ![]() или
или ![]() равно +¥ или –¥.
равно +¥ или –¥.
Замечание 2. Непрерывные функции вертикальных асимптот не имеют.
*4. Прямая y=kx+b называется наклонной асимптотой графика функции y=f(x) при xà+¥(–¥), если f(x)=kx+b+a(x), где![]()
Т3. Прямая y=kx+b называется наклонной асимптотой графика функции y=f(x) при xà+¥(–¥), тогда и только тогда, когда существуют ![]() ,
, ![]() , причем при xà+¥(–¥) наклонная асимптота называется правой (левой). Док-во: Предположим, что кривая y=f(x) имеет наклонную асимптоту y=kx+b при xà+¥, т.е. имеет место равенство f(x)=kx+b+a(x). Тогда
, причем при xà+¥(–¥) наклонная асимптота называется правой (левой). Док-во: Предположим, что кривая y=f(x) имеет наклонную асимптоту y=kx+b при xà+¥, т.е. имеет место равенство f(x)=kx+b+a(x). Тогда ![]() . Переходя к пределу при xà+¥, получаем
. Переходя к пределу при xà+¥, получаем ![]() . Далее из f(x)=kx+b+a(x)à b=f(x)-kx-a(x). Переходя к пределу при xà+¥, получаем
. Далее из f(x)=kx+b+a(x)à b=f(x)-kx-a(x). Переходя к пределу при xà+¥, получаем ![]() . Докажем обратное утверждение. Пусть пределы, указанные в теореме, существуют и конечны. Следовательно, f(x)–kx=b+a(x), где a(x)à0, при xà+¥(–¥). Отсюда и получаем представление f(x)=kx+b+a(x). Теорема доказана.
. Докажем обратное утверждение. Пусть пределы, указанные в теореме, существуют и конечны. Следовательно, f(x)–kx=b+a(x), где a(x)à0, при xà+¥(–¥). Отсюда и получаем представление f(x)=kx+b+a(x). Теорема доказана.
Замечание3. При k=0 прямая y=b называется горизонтальной асимптотой, причем при xà+¥(–¥) – правой (левой).
2.
*1. Точку х0 назовем стандартной для функции f(x), если f(x) дифференцируема в точке x0 и f¢(x0)=0.
*2. Необходимое условие экстремума. Если функция y=f(x) имеет в точке x0 локальный экстремум, то либо x0 – стационарная точка, либо f не является дифференцируемой в точке x0.
Замечание 1. Необходимое условие экстремума не является достаточным.
Т1. (Первое достаточное условие экстремума). Пусть y=f(x) дифференцируема в некоторой окрестности точки x0, кроме, быть может, самой точки x0, в которой она является непрерывной. Если при переходе x через x0 слева направо f¢(x) меняет знак с + на –, то точка x0 является точкой максимума, при перемене знака с – на + точка x0 является точкой минимума. Док-во: Пусть xÎ(a,b), x¹x0, (a,b) – достаточно малая окрестность точки x0. И пусть, например, производная меняет знак с + на –. Покажем что f(x0)>f(x). По теореме Лагранжа (применительно к отрезку [x,x0] или [x0,x]) f(x)–f(x0)=(x- x0)f¢(a), где a лежит между x0 или x: а) x< x0Þx- x0<0, f¢(a)>0Þf(x)–f(x0)<0Þf(x0)>f(x); б) x>x0Þx–x0>0, f¢(a)<0Þf(x)–f(x0)<0Þf(x0)>f(x).
Замечание 2. Если f¢(x) не меняет знака при переходе через точку х0, то х0 не является точкой экстремума.
Т2. (Второе достаточное условие экстремума). Пусть x0 – стационарная точка функции y=f(x), которая имеет в точке x0 вторую производную. Тогда: 1) f¢¢( x0)>0Þf имеет в точке x0 локальный минимум. 2) f¢¢( x0)<0Þf имеет в точке x0 локальный максимум.
3.
*1. График функции y=f(x) называется выпуклым вниз (или вогнутым вверх) в промежутке (a,b), если соответствующая дуга кривой расположена выше касательной в любой точке этой дуги.
*2. График функции y=f(x) называется выпуклым вверх (или вогнутым вниз) в промежутке (a,b), если соответствующая дуга кривой расположена ниже касательной в любой точке этой дуги.
Т1. Пусть y=f(x) имеет на (a,b) конечную 2-ю производную. Тогда: 1) f¢¢(x)>0, "xÎ(a,b)Þграфик f(x) имеет на (a,b) выпуклость, направленную вниз; 2) ) f¢¢(x)<0, "xÎ(a,b)Þграфик f(x) имеет на (a,b) выпуклость, направленную вверх
*3. Точка (c,f(с)) графика функций f(x) называется точкой перегиба, если на (a,c) и (c,b) кривая y=f(x) имеет разные направления выпуклости ((a,b) – достаточно малая окрестность точки c).
Т2. (Необходимое условие перегиба). Если кривая y=f(x) имеет перегиб в точке (c, f(c)) и функция y=f(x) имеет в точке c непрерывную вторую производную, то f¢¢(c)=0.
Замечание1. Необходимое условие перегиба не является достаточным.
Замечание2. В точке перегиба вторая производная может не существовать.
Т3. (Первое достаточное условие перегиба). Пусть y=f(x) имеет вторую производную на cÎ(a,b), f¢¢(c)=0. Если f¢¢(x) имеет на (a,c), (c,b) разные знаки, то (c, f(c)) – точка перегиба графика f(x).
Т4. (Второе условие перегиба). Если y=f(x) имеет в точке конечную третью производную и f¢¢(c)=0, а f¢¢¢(c)¹0, тогда (c, f(c)) – точка перегиба графика f(x).
4.
*1. Первообразная от функции f(x) в данном интервале называется функция F(x), производная которой равна данной функции: F¢(x)=f(x).
T1. Всякая непрерывная функция имеет бесчисленное множество первообразных, причем любые две из них отличаются друг от друга только постоянным слагаемым. Док-во: F(x) и Ф(х) – две первообразные от f(x), тождественно не равные между собой. Имеем F¢(x)=f(x), Ф¢(х)=f(x). Вычитая одно равенство из другого, получим [F(x)–Ф(х)]¢=0. Но если производная от некоторой функции (в нашем случае от F(x)–Ф(х)) тождественно равна нулю, то сама функция есть постоянная; Þ F(x)–Ф(х)=С.
*2. Неопределенным интегралом от данной функции f(x) называется множество всех его первообразных ![]() ,где F¢(x)=f(x).
,где F¢(x)=f(x).
5.
Свойства неопределенного интеграла:
Производная НИ =подынтегральной функции; дифференциал от НИ равен подынтегральному выражению:Т2. (об инвариантности формул интегрирования): Пусть òf(x)dx=F(x)+C – какая-либо известная формула интегрирования и u=ф(х) – любая функция, имеющая непрерывную производную. Тогда òf(u)du=F(u)+C. Док-во: Из того, что òf(x)dx=F(x)+C, следует F¢(x)=f(x). Возьмем функцию F(u)=F[ф(x)]; для её дифференциала, в силу теоремы об инвариантности вида первого дифференциала функции, имеем: dF(u)=F¢(u)du=f(u)du. Отсюда òf(u)du=òdF(u)=f(u)+C.
6.
Метод замены переменных.
1) Подведение под знак дифференциала. Т1. Пусть функция y=f(x) определена и дифференцируема, пусть также существует f(x)=f(j(t)) тогда если функция f(x) имеет первообразную то справедлива формула: ![]() –формула замены переменных. Док-во: пусть F(x) для функции f(x), т.е. F¢(x)=f(x). Найдем первообразную для f(j(t)), [F(j(t))]¢t=F¢(x)(j(t)) j¢(t)=F¢(x) j¢(t)=f(x) j¢(t). òf(x) j¢(t)dt=f(j(t))+C. F(j(t))+C=[F(x)+C]|x=j(t)=òf(x)dx|x=j(t).
–формула замены переменных. Док-во: пусть F(x) для функции f(x), т.е. F¢(x)=f(x). Найдем первообразную для f(j(t)), [F(j(t))]¢t=F¢(x)(j(t)) j¢(t)=F¢(x) j¢(t)=f(x) j¢(t). òf(x) j¢(t)dt=f(j(t))+C. F(j(t))+C=[F(x)+C]|x=j(t)=òf(x)dx|x=j(t).
Замечание1. При интегрировании иногда целесообразно подбирать подстановку не в виде x=j(t), а в виде t=j(x).
2) Подведение под знак дифференциала. F(x)dx=g(j(x)) j¢(x)dx=g(u)du. òf(x)dx=òg(j(x)) j¢(x)dx=òg(u)du.
dx=d(x+b), где b=const; dx=1/ad(ax), a¹0; dx=1/ad(ax+b), a¹0; ф¢(х)dx=dф(x); xdx=1/2 d(x2+b); sinxdx=d(-cosx); cosxdx=d(sinx);Интегрирование по частям: òudv=uv-òvdu. До-во: Пусть u(x) и v(x) – функции от х с непрерывными производными. D(uv)=udv+vdu,Þudv=d(uv)-vduÞ(интегрируем) òudv=òd(uv)-òvdu или òudv=uv-òvdu.
7.
Интегрирование по частям: òudv=uv-òvdu. До-во: Пусть u(x) и v(x) – функции от х с непрерывными производными. D(uv)=udv+vdu,Þudv=d(uv)-vduÞ(интегрируем) òudv=òd(uv)-òvdu или òudv=uv-òvdu.
Интегрирование функций, содержащих квадратный трехчлен:
![]()
![]()
Первый интеграл табличного вида: òdu/uk:![]()
Второй интеграл сводится к нахождению интеграла: где u=x+p/2, a=![]() , q-p2/4>0
, q-p2/4>0 ![]()
![]()
![]() – рекуррентная формула.
– рекуррентная формула.
Интегрирование рациональных функций: R(x)=P(x)/Q(x), R(x)-рациональная функция, P(x) и Q(x)-многочлены. Дробь P(x)/Q(x) можно разложить в сумму простейших дробей, где Ai, Bi, Ci – постоянные, а именно: каждому множителю (x-a)k в представлении знаменателя Q(x) соответствует в разложении дроби P(x)/Q(x) на слагаемые сумма k простейших дробей типа ![]() а каждому множителю (x2+px+q)t соответствует сумма t простейших дробей типа
а каждому множителю (x2+px+q)t соответствует сумма t простейших дробей типа ![]() . Таким образом при разложении знаменателя Q(x) на множители имеет место разложение дроби P(x)/Q(x) на слагаемые.
. Таким образом при разложении знаменателя Q(x) на множители имеет место разложение дроби P(x)/Q(x) на слагаемые.
![]()
Правила интегрирования рациональных дробей:
Если рац. дробь неправильная, то её представляют в виде суммы многочлена и неправильной дроби. Разлагают знаменатель правильной дроби на множетели.Правую рац. дробь разлагают на сумму простейших дробей. Этим самым интегрирование правильной рац. дроби сводят к интегрированию простейших дробей.
8.
Интегрирование тригонометрических функций:
I. 1 Интеграл вида: 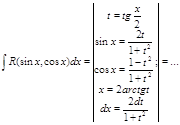
2 R(sinx, cosx) – нечетная функция относительно sinx, то cosx=t.
3 R(sinx, cosx) – нечетная функция относительно cosx, то sinx=t.
4 R(sinx, cosx) – нечетная функция относительно sinx и cosx, то tgx=t. 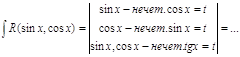
II. 1 ![]()
2 Оба показателя степени m и n – четные положительные числа: sinxcosx=1/2 sin2x; sin2x=1/2(1-cos2x); cos2x=1/2(1+cos2x).
III. òtgmxdx и òctgmxdx, где m-целое положительное число. tg2x=sec2x-1 или ctg2x=cosec2x –1.
IV. òtgmxsecnxdx и òctgmxcosecnxdx, где n – четное положительное число. sec2x=1+tg2x или cosec2x=1+ctg2x.
V. òsinmx*cosnxdx, òcosmx*cosnxdx, òsinmx*sinnxdx; sinacosb=1/2(sin(a+b)+sin(a-b)); cosacosb=1/2(cos(a+b)+cos(a-b)); sinasinb=1/2(cos(a-b)-cos(a+b));
9.
Интегрирование иррациональных функций:
I. 1 òR(x, ![]() ,
, ![]() ,…)dx, k-общий знаменатель дробей m/n, r/s…. x=tk, dx=ktk–1dt
,…)dx, k-общий знаменатель дробей m/n, r/s…. x=tk, dx=ktk–1dt
2 òR(x,![]() ,
, ![]() …)dx,
…)dx, ![]() , x=
, x=![]() , dx=
, dx=![]()
II. 1 ![]() Вынести 1/Öa или 1/Ö-a. И выделим полные квадраты.
Вынести 1/Öa или 1/Ö-a. И выделим полные квадраты.
2 ![]()
3 ![]() Разбить на два интеграла.
Разбить на два интеграла.
4 ![]()
![]()
III. 1 ![]()
2 ![]()
3 ![]()
![]() 1)p-целое число x=tS, где s- наименьшее общее кратное знаменателей у дробей m и n. 2) (m+1)/n –целое число: a+bxn=tS; 3) p+(m+1)/n-целое число: a-n+b=tS и где s- знаменатель дроби p.
1)p-целое число x=tS, где s- наименьшее общее кратное знаменателей у дробей m и n. 2) (m+1)/n –целое число: a+bxn=tS; 3) p+(m+1)/n-целое число: a-n+b=tS и где s- знаменатель дроби p.
10.
Определенный интеграл:
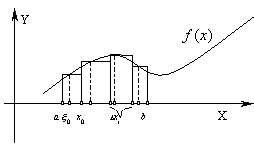
1) интервал [a,b], в котором задана функция f(x), разбивается на n частичных интервалов при помощи точек a=x0<x1<…<xn–1<xn=b;
2) Значение функции f(xI) в какой нибудь точке xiÎ[xi–xi–1] умножается на длину этого интервала xi–xi–1, т.е. составляется произведение f(xi)(xi–xi–1);
3) ![]() , где xi–xi–1=Dxi;
, где xi–xi–1=Dxi;
I=![]() – этот предел (если он существует) называется определенным интегралом, или интегралом от функции f(x) на интервале [a,b], обозначается
– этот предел (если он существует) называется определенным интегралом, или интегралом от функции f(x) на интервале [a,b], обозначается ![]()
*1. Определенным интегралом называется предел интегральной суммы ![]() при стремлении к нулю длинны наибольшего частичного интеграла (в предположении, что предел существует).
при стремлении к нулю длинны наибольшего частичного интеграла (в предположении, что предел существует).
Т1. (Необходимое условие существования интеграла): Если ОИ существует, т.е. функция f(x) интегрируема не [a,b], то f(x) ограничена на этом отрезке. Но этого не достаточно. Док-во: Функция Дирихле: ![]()
Похожие работы
... функции f(x), g(x) интегрируемы на [a;b], тогда интегрируема на [a;b] их сумма и разность , 3. Если , то: 4. Если функция f(x) интегрируема на [a;b] и a<c<b, то , т.е. интеграл по всему отрезку равен сумме интегралов по частям этого отрезка. Это св-во наз-ют аддивностью определенного интеграла. Сравнение определённых интегралов Если - интегрируема на и , то: . Если - интегрируема ...
... десятичной дробью, такие как π , , и т.д. 5) комплексные числа, вводящие в рассмотрение «мнимое число» . История развития числа от целого числа до иррационального знакома нам по школьному курсу. С эпохи Возрождения математики стали использовать числа вида z = x+iy для решения квадратных уравнений, дискриминант у которых отрицателен, где i =, i² = –1, х и у – вещественные числа Само ...
... ; U’V+UV’+UV*P(x)=Q(x) ; U’V+U(V’+V*P(x))=Q(x) Найдём V ,чтобы V’+VP(x)=0 : Тогда U’V=Q(x) y’+y cos(x)=1/2 sin(2x) y=UV U’V+UV’+UVcos(x)=sin(x)cos(x) V’+Vcos(x)=0 dV/V=-cos(x)dx ln(V)= -sin(x) V=e-sin(x) sin(x)=t Билет №22 Уравнение Бернулли и Рикотти и их решение. Уравнение Бернулли – это диф. Ур-е следующего вида : где P(x) и Q(x) – непрерывные функции m – ...
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...


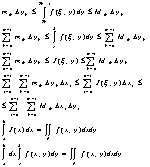


0 комментариев