Навигация
Записать исходный вид функции
7. Записать исходный вид функции.
Метод неопределенных коэффициентов применим для дизъюнктивной формы и непригоден для конъюнктивной.
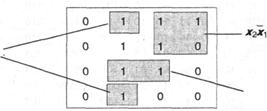
Пример:
![]()
|
|
|
|
|
|
|
|
| |
| 0 | 0 | 0 | 0 | 00 | 00 | 00 | 000 | 1 |
| 1 | 0 | 0 | 1 | 00 | 01 | 01 | 001 | 0 |
| 2 | 0 | 1 | 0 | 01 | 00 | 10 | 010 | 1 |
| 3 | 0 | 1 | 1 | 01 | 01 | 11 | 011 | 0 |
| 4 | 1 | 0 | 0 | 10 | 10 | 00 | 100 | 1 |
| 5 | 1 | 0 | 1 | 10 | 11 | 01 | 101 | 0 |
| 6 | 1 | 1 | 0 | 11 | 10 | 10 | 110 | 0 |
| 7 | 1 | 1 | 1 | 11 | 11 | 11 | 111 | 1 |
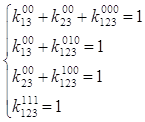
Итак, получим ![]()
Метод Квайна (1.3)
Суть метода сводится к тому, чтобы преобразовать ДСНФ в МДНФ. Задачи минимизации по методу Квайна состоит в попарном сравнении импликант, входящих в ДСНФ с целью выявления возможности склеивания по какой-то пременной так:
![]()
Таким образом, можно понизить ранг термов. Процедура производится до тех пор, пока не остается ни одного терма, допускающего склейки с другим. Причем склеивающиеся термы помечаются *.
Определение: Непомеченные термы называются первичными импликантами.
Полученное логическое выражение не всегда оказывается минимальным, поэтому исследуется возможность дальнейшего упрощения.
Для этого:
1. Составляются таблицы, в строках которых пишутся найденные первичные импликанты, а в столбцах указываются термы первичной ФАЛ.
2. Клетки этой таблицы отмечаются в том случае, если первичная импликанта входит в состав какого-нибудь первичного терма.
3. Задача упрощения сводится к нахождению такого минимального количества импликант, которые покрывают все столбцы.
Алгоритм метода Квайна (шаги):
1. Нахождение первичных импликант.
Исходные термы из ДНФ записывают в столбик и склеиваю сверху вниз. Непомеченные импликанты переходят в функции на этом шаге.
2. Расстановка меток избыточности.
Составляем таблицу, в которой строки – первичные импликанты, столбцы – исходные термы. Если некоторый min-терм содержит первичный импликант, то на пересечении строки и столбца ставим метку.
3. Нахождение существенных импликант.
Если в каком-либо столбце есть только одна метка, то первичный импликант соответствующей строки является существенным.
4. Строка, содержащая существенный импликант и соответствующие столбцы вычеркиваются.
Если в результате вычеркивания столбцов появятся строки первичных импликант, которые не содержат метки или содержат одинаковые метки в строках, то такие первичные импликанты вычеркиваются. В последнем случае оставляем одну меньшего ранга.
Похожие работы
... 0 и 1: . 10. Законы Блейка-Порецкого: . 11. Связь импликации с отрицанием – и дизъюнкцией : . 12. Связь эквивалентности ~ с дизъюнкцией , конъюнкцией и отрицанием: ~ y =. Всякая функция алгебры логики может быть реализована некоторой формулой языка с символами ~, –. 1.2 Дизъюнктивные и конъюнктивные нормальные формы (ДНФ и КНФ) ДНФ и КНФ играют особую роль в алгебре ...
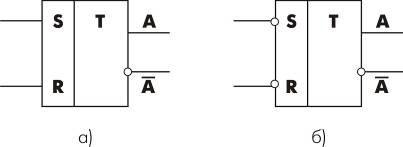
... схемами с односторонней проводимостью, имеющими конечное число входов и один выход. Простейшие электронные схемы, реализующие элементарные булевы функции (НЕ, И, ИЛИ, ИЛИ-НЕ, И-НЕ), называются логическими элементами (ЛЭ). Аналитическая форма представления булевых функций При решении конкретных технических задач булевы функции, отражающие логические связи, наиболее часто задаются в табличной ...
... ответ на этот вопрос положителен. Штрих Шеффера является отрицанием конъюнкции, стрелка Пирса – отрицание дизъюнкции, сумма Жегалкина – отрицание эквивалентности. М. Жегалкин (1869–1947) – российский математик и логик, один из основоположников современной математической логики. Чарльз Пирс (1839–1914) – американский логик, математик и естествоиспытатель. Основоположник семиотики, родоначальник ...
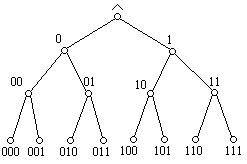
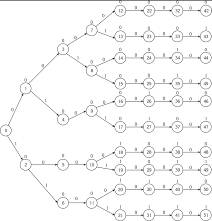
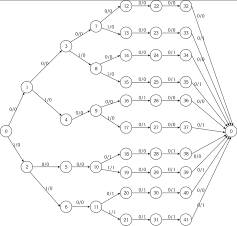
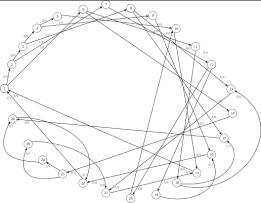
... , и, обратно, для любого автомата Мура существует эквивалентный ему автомат Мили. Таким образом, возможны взаимные трансформации автоматов. Граф-дерево автомата Мили. 10 В ходе этапа построения кодопреобразователя осуществляется преобразование графа-дерево автомата Мура в граф-дерево автомата Мили. Для этого все конечные состояния автомата Мура заменяются нулевым состоянием. Граф-дерево ...


0 комментариев