Определить точечные оценки (среднее, дисперсия)

1.2 Определить точечные оценки (среднее, дисперсия).

Среднее значение:

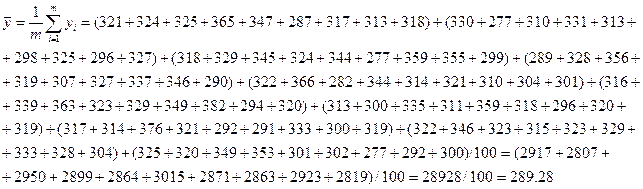
Дисперсия:

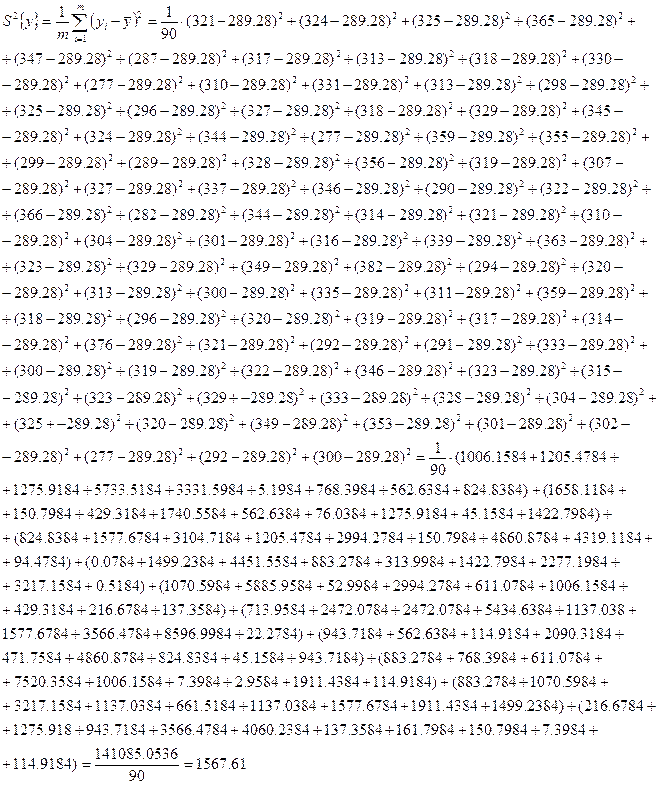
1.3 Определить относительные ошибки и доверительные интервалы для генерального среднего и генеральной дисперсии.

Абсолютная доверительная ошибка среднего:

при ,

Относительная доверительная ошибка среднего:

Границы доверительного интервала среднего значения:

Абсолютная доверительная ошибка дисперсии:

 – относительная доверительная ошибка

дисперсии

Граница доверительного интервала дисперсии:

1.4 Спланировать объём выборки, если при определении среднего относительная ошибка не должна превышать 1%.

Для планирования объёма выборки из В₁ выбираем 3 значения: 314, 322, 321.

Выборка В^*.

Числовые характеристики В^*:

 – среднее значение

Дисперсия:

Среднее квадратичное отклонение:

Квадратичная неровнота:

Абсолютная доверительная ошибка:

где ; ;

Относительная доверительная ошибка:

Доверительный объём измерений:

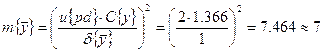
Реализуем выборку объёма . Для этого выбираем 2 значения: 324, 325, 319, 315, 311, 317, 313.

Выборка В^**.

Числовые характеристики В^**:

 – среднее значение

Дисперсия:

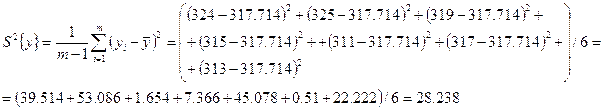
Среднее квадратичное отклонение:

Квадратичная неровнота:

Абсолютная доверительная ошибка:

где ; ;

Относительная доверительная ошибка:

1.5 Проверить гипотезу о пропорциональности технологического параметра для заданной выборки.

Проверка гипотезы осуществляется по критерию х²:

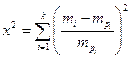
где  – объём выборки;  – частота попадания в i – классе; k – число классов;   – вероятность попадания в i – интервал.

где ;  – число степени свободы

Рассмотрим гипотезу , при конкурирующей

Введём новое значение , где ;

i	интервал
1	277-292	284.5	0.31	0.07	0.1217	0.0279	0.0938	8.442	1.558	0.184
2	292-307	299.5	0.07	0.45	0.0279	0.1736	0.1457	13.113	0.887	0.068
3	307-322	314.5	0.45	0.83	0.1736	0.2967	0.1231	11.079	14.921	1.347
4	322-337	329.5	0.83	1.205	0.2967	0.3944	0.0977	8.793	12.207	1.388
5	337-352	344.5	1.205	1.58	0.3944	0.4429	0.0485	4.365	4.635	1.062
6	352-367	359.5	1.58	1.96	0.4429	0.4750	0.0321	2.889	5.111	1.769
7	367-382	374.5	1.96	2.34	0.4750	0.4903	0.0153	1.377	0.623	0.452
										6.27

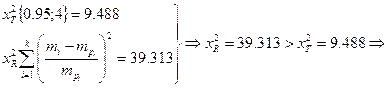 гипотеза о нормальности технологического процесса  не принимается.

1.6 Проверить наличие резко выделяющихся значений в выборке (метод ).

 и  находятся в пределах интервала (; ), следовательно резко выделяющихся значений в выборке нет.