Навигация
Обработка сравнительного технологического эксперимента
2. Обработка сравнительного технологического эксперимента.
Подготовка данных: сформировать из исходного массива В1 методом рандомизации две выборки малого объёма ![]() В2 и В3 для дальнейших исследований.
В2 и В3 для дальнейших исследований.
2.1 Определить числовые характеристики выборок В2 и В3.
|
| В2 | В3 |
| 1 | 347 | 287 |
| 2 | 313 | 298 |
| 3 | 344 | 277 |
| 4 | 307 | 327 |
| 5 | 314 | 321 |
| 6 | 329 | 349 |
| 7 | 359 | 318 |
| 8 | 292 | 291 |
| 9 | 323 | 329 |
| 10 | 301 | 302 |
Числовые характеристики выборки В2.
Среднее значение:
 Дисперсия:
Дисперсия:
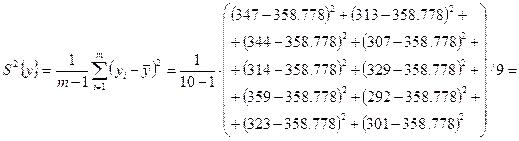
![]()
Среднее квадратичное отклонение:
![]()
Коэффициент вариации:
![]()
Квадратичная неровнота:
![]()
Абсолютная доверительная ошибка среднего значения:
![]()
где ![]() ;
; ![]() ;
; ![]()
Относительная доверительная ошибка среднего значения:
![]()
Числовые характеристики выборки В3.
Среднее значение:
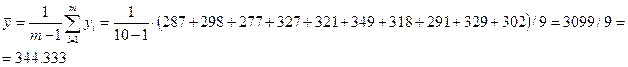
Дисперсия:
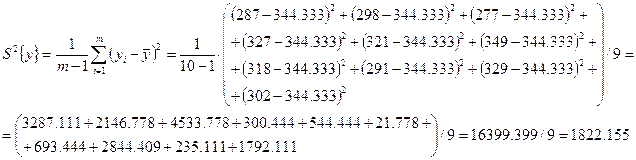
Среднее квадратичное отклонение:
![]()
Коэффициент вариации:
![]()
Квадратичная неровнота:
![]()
Абсолютная доверительная ошибка среднего значения:
![]()
где ![]() ;
; ![]() ;
; ![]()
Относительная доверительная ошибка среднего значения:
![]()
2.2 Определить доверительные интервалы для генерального среднего и генеральной дисперсии.
Доверительный интервал для среднего значения выборки В2:
![]()
![]()
![]()
Доверительный интервал для дисперсии:
![]()
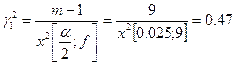 ;
; 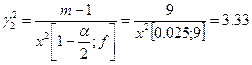
где ![]() ;
; ![]()
![]()
![]()
Доверительный интервал для среднего значения выборки В3:
![]()
![]()
![]()
Доверительный интервал для дисперсии:
![]()
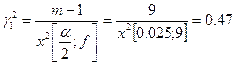 ;
; 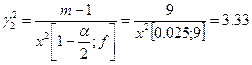
где ![]() ;
; ![]()
![]()
![]()
2.3 Проверка гипотезы о равенстве генеральных средних выборок В2 и В3: ![]() ;
; ![]() .
.
Сравниваем две дисперсии нормальных генеральных совокупностей с числом степеней свободы:
![]() ;
; ![]()
![]() ;
; ![]()
Оцениваем возможность принятия гипотезы ![]() .
.
При альтернативной гипотезе ![]() и доверительной вероятности
и доверительной вероятности ![]() находим:
находим:
![]()
![]()
т.к. ![]() , то выдвинутую гипотезу об однородности дисперсии или равной точности двух рядов измерений
, то выдвинутую гипотезу об однородности дисперсии или равной точности двух рядов измерений ![]() и
и ![]() надо принять.
надо принять.
Сравниваем две средние из нормальных распределений генеральных совокупностей.
Если ![]() доказана, то используется критерий
доказана, то используется критерий ![]() :
:
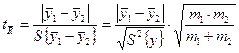 ,
,
где 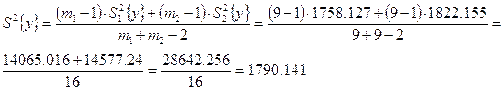
![]() ;
; ![]() ;
; ![]()
![]() ;
; ![]() ;
; ![]()
Проверим гипотезу о равенстве средних:
![]() при конкурирующей гипотезе
при конкурирующей гипотезе
![]()
Затем находим расчётное значение критерия Стьюдента:
![]()
и его табельное значение ![]()
Т.к. ![]() , то генеральные средние
, то генеральные средние ![]() и
и ![]() статически не различаются. Гипотеза
статически не различаются. Гипотеза ![]() принимается.
принимается.
Похожие работы
... . Анализ исследований, выполненных по вопросу оценивания и оценки, продемонстрировал неординарность этой проблемы для науки в целом и актуальность изучения оценочной функции психики для решения теоретических и практических задач, стоящих перед различными психологическими дисциплинами и общей психологией. При этом была обоснована необходимость начать теоретический анализ с обоснования сущности ...
... - учителю. У учащихся формируется познавательный мотив, они более самостоятельны в выборе решения. Заключение и выводы В теоретической части мы рассмотрели учебно-познавательную мотивацию младшего школьника и оценочную деятельность учителя, их взаимоотношение. Теоретическая часть базируется на исследованиях А.Н. Леонтьева, Л.С. Выготского, Л.И. Божович, Ш.А. Амонашвили и др. Анализ ...
... предсказуемы. Данный метод наиболее применим к предприятиям, приносящим стабильную прибыль, величина которой из года в год меняется незначительно (или темпы роста прибыли постоянны). В отличие от оценки недвижимости, в оценке бизнеса предприятий данный метод применяется довольно редко и в основном для мелких предприятий, из - за значительных колебаний величин прибылей или денежных потоков по годам ...
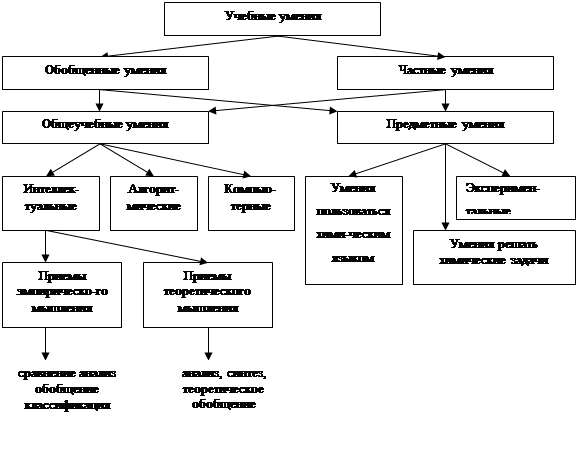
... "ОВР" можно свести в единую схему [13] , которая отражает их взаимосвязь (таблица 3). Таблица 3. Понятия об окислительно-восстановительных реакциях Умения пользоваться химическим языком I группа II группа Относительная электроотрицательность исление1восстановление1 степень окисления окисление2 восстановление2 окислитель восстановитель единство окисления и восстановления ОВР ...



0 комментариев