Навигация
Метод усреднения Ван-дер-Поля
1.1. Метод усреднения Ван-дер-Поля.
В своих исследованиях Ван-дер-Поль рассматривал, главным образом, уравнения с малым положительным параметром ε вида
![]() (1)
(1)
Оно описывает всякого рода колебательные движения в среде низкого сопротивления.
Уравнение (1) условимся называть квазилинейным, а колебания, которые оно описывает, — квазилинейными колебаниями. Функция f может быть весьма общего вида и, в частности, даже разрывной.
Уравнение
![]() (1.2)
(1.2)
называется порождающим. Оно описывает гармонические колебания. Общее решение этого уравнения:
х=acos(ωt+φ),
оно описывает некоторый колебательный процесс, обладающий частотой ω. Естественно предположить, что в случае малых значений ε решение уравнения (1) будет описывать также некоторый колебательный процесс.
Для получения приближенного решения уравнения (1) при достаточно малых значениях параметра ε Ван-дер-Поль предложил особый прием, названный им методом «медленно меняющихся» коэффициентов, аналогичный одному из методов, применявшихся еще Лагранжем в небесной механике. Он представил истинное решение уравнения (1) в виде функции, выражающей гармонические колебания:
х=acos(ωt+φ) (2)
с медленно меняющимися амплитудой а и фазой φ, которые должны находиться из системы дифференциальных уравнений с разделяющимися переменными:
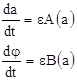 ,
(3)
,
(3)
составленными по определенному правилу. Уравнения (3), так называемые «укороченные уравнения» Ван-дер-Поля, позволяют сравнительно просто получить приближенное решение исходного уравнения (1). В частности, задача отыскания периодического решения уравнения (1) сводится к значительно более простой задаче нахождения состояния равновесия системы, описываемой «укороченными уравнениями» (3).
Перейдем к составлению «укороченных уравнений» для рассматриваемого уравнения (1), или эквивалентной ему системы двух уравнений первого порядка
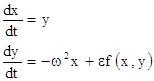 (4)
(4)
Прежде всего, заметим, что при ε=0 уравнение (1) превращается в дифференциальное уравнение обычного гармонического осциллятора, и тогда решение системы (4) имеет вид:
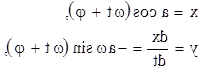 (5)
(5)
где а и φ— постоянные интегрирования.
Будем отыскивать решение уравнения (4) при достаточно малых значениях параметра ε в виде выражений (5), но уже считая а и φ не постоянными, а некоторыми функциями времени. Для этого будем рассматривать выражения (5) не как решения уравнения (4) при ε = 0, а как формулы замены старых переменных х и у на новые переменные а и φ.
Сделаем замену: ![]() .
.
Продифференцировав выражения (5) по t, подставим значения производных в уравнениях (4). Принимая во внимание формулы (5), получаем систему уравнений относительно производных, новых переменных а и φ:
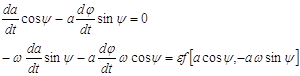 (6)
(6)
разрешая систему (6) относительно ![]() и
и ![]() , находим систему уравнений:
, находим систему уравнений:
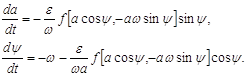 (7)
(7)
Система дифференциальных уравнений (7) эквивалентна рассматриваемой исходной системе (4) или, что то же самое, уравнению (1) .
Из системы (7) видно, что медленные и быстрые движения для ![]() разделены.
разделены.
Усредняя правые части системы (7) мы получим (8):
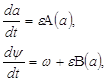 (8)
(8)
где принято обозначение ![]()
Таким образом, «укорочёнными уравнениями» для системы (7) являются уравнения (3), где
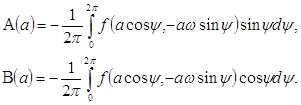 (9)
(9)
Уравнения (8) будем называть укороченными уравнениями или уравнениями Ван-дер-Поля. Они значительно проще исходной системы (7), поскольку первое уравнения может быть проинтегрировано независимо от второго. В системе (8) медленные и быстрые движения для ![]() разделены.
разделены.
Интегрируя первое из уравнений этой системы, мы находим закон изменения амплитуды. Очень часто в прикладных задачах бывает достаточно найти только зависимость амплитуды от времени. В рассматриваемой теории для этого достаточно найти решение уравнения первого порядка (в общем случае нелинейного).
Определение фазы сводится к квадратурам. Наибольший интерес обычно представляет не сама фаза, а скорость ее изменения в зависимости от амплитуды. Ответ на этот вопрос дает непосредственно второе уравнение системы (8).
Итак, метод Ван-дер-Поля решения уравнения (1) состоит в переходе от переменной х и y к переменным а и ![]() (которые мы будем называть переменными Ван-дер-Поля) и к замене точных уравнений (7) укороченной системой (8).
(которые мы будем называть переменными Ван-дер-Поля) и к замене точных уравнений (7) укороченной системой (8).
Система (8) позволяет найти возможные стационарные (автоколебательные) режимы, т.е. режимы, при которых амплитуда остается неизменной. Полагая ![]() , находим, что стационарная амплитуда должна быть корнем трансцендентного уравнения
, находим, что стационарная амплитуда должна быть корнем трансцендентного уравнения
![]() (10)
(10)
Заметим, что уравнение (10) совпадает с одним из тех уравнений, которое мы получили бы, если бы рассматривали уравнение (1) как квазилинейное и разыскивали периодические решения методом Пуанкаре.
Трансцендентное уравнение (10) может совсем не иметь действительных решений. Это будет означать, что в системе стационарные колебания невозможны. Уравнение (10) может иметь одно или несколько решений, в случаях консервативных систем оно удовлетворяется тождественно. В самом деле, в этом случае функция f зависит только от переменной x, поэтому уравнение (10) примет вид:
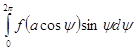 (10а)
(10а)
Так как ![]() , то под знаком интеграла стоит полный дифференциал:
, то под знаком интеграла стоит полный дифференциал:
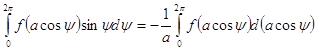
Обозначим через F![]() — неопределенный интеграл
— неопределенный интеграл 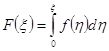 .
.
Тогда 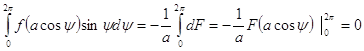 ,
,
то есть уравнение (10а) удовлетворяется тождественно по ![]() .
.
Обоснование метода Ван-дер-Поля
Л. И. Мандельштамом и Н. Д. Папалекси.
Рассмотрим систему стандартного вида
![]() (s=1,2) (1)
(s=1,2) (1)
Уравнение Ван-дер-Поля также можно привести к системе стандартного вида:
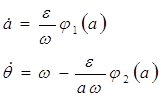 (2)
(2)
Сделаем замену
![]() ,
,
тогда: 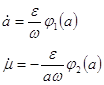 (3)
(3)
Будем считать ![]() =
=![]() .
.
Среднее значение функции ![]() за период 2
за период 2![]() :
:
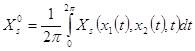
При этом усреднении интегрирование ведется по третьей переменной t в предположении, что ![]() и
и ![]() от t не зависят.
от t не зависят.
![]()
Наряду с точной системой рассматривается приближенная
![]() , (s=1,2).
, (s=1,2).
Обе системы, приближенная и точная, решаются при начальных условиях
![]() (4)
(4)
Для задач Коши (1) и (4), (3) и (4) справедлива следующая теорема:
Теорема. Пусть при всех t и в некоторой области переменных ![]() функции
функции ![]() непрерывны и ограничены. Функции
непрерывны и ограничены. Функции ![]() также непрерывны и ограничены в области Г.
также непрерывны и ограничены в области Г. ![]() — 2
— 2![]() -периодические по t. Функции
-периодические по t. Функции ![]() и
и ![]() — удовлетворяют условию Липшица по переменным
— удовлетворяют условию Липшица по переменным ![]() и
и ![]() (при этих условиях существует и единственно решение). Тогда для
(при этих условиях существует и единственно решение). Тогда для![]()
![]() и L>0:
и L>0:
![]() (5)
(5)
0![]() (6)
(6)
Доказательство:
Решение задач Коши (1) и (4), (3) и (4) существует и единственно. Поэтому решение (1) и (4) будем искать методом приближений.
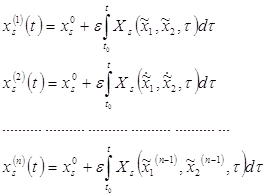
Обозначим
![]() (*)
(*)
Функция ![]()
![]() — 2
— 2![]() -периодическая по
-периодическая по ![]() .
.
Пусть
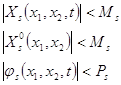 (7)
(7)
![]() удовлетворяет условиям Липшица по переменным
удовлетворяет условиям Липшица по переменным ![]() и
и![]() . Проинтегрируем функцию
. Проинтегрируем функцию ![]() :
:
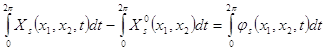 .
.
Интеграл 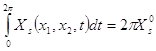 и
и 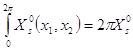 поэтому
поэтому

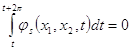 (7a)
(7a)
В промежутке ![]() находятся те значения t, для которых будет существовать решение (1) - (4) и оно не выйдет за пределы области G. Это характеризуется так
находятся те значения t, для которых будет существовать решение (1) - (4) и оно не выйдет за пределы области G. Это характеризуется так
![]()
Из теоремы Пикара следует, что при всех таких t приближенное выражение сходится к решению задачи Коши:
![]()
![]()
![]()
![]() — целую часть от деления обозначим N. Тогда
— целую часть от деления обозначим N. Тогда ![]() — дробная часть
— дробная часть ![]()
![]() ,
,
где ![]() — остаточный интервал.
— остаточный интервал.
С учетом возможности такого разбиения
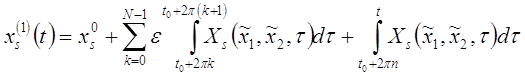
Если рассмотреть ![]() , то последнее выражение перепишется в виде:
, то последнее выражение перепишется в виде:
![]() =
=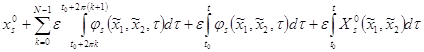 ,
,
где с учетом (4)
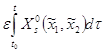 =
=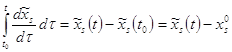
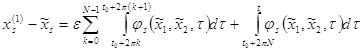
Рассмотрим интеграл при ![]()
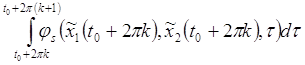
![]() и
и ![]() от
от ![]() не зависят. Из равенств (7а) следует, что последнее выражение равно нулю
не зависят. Из равенств (7а) следует, что последнее выражение равно нулю ![]() .
.
Вычислим
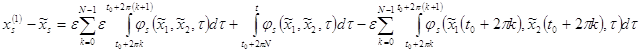
То есть
![]()
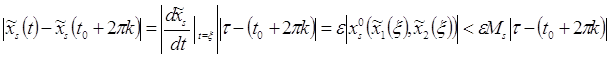
![]()
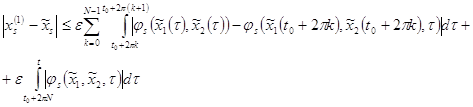 (8)
(8)
Мы можем сказать, что в (8), все, что стоит под знаком суммы
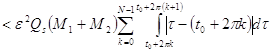
Так как
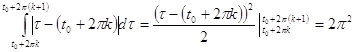 ,
,
то последнее неравенство равносильно следующему:
![]()
![]()
![]()
![]()
![]()
![]() Поэтому:
Поэтому:
![]()
![]() =
=![]() , (9)
, (9)
![]() где
где ![]()
![]()
![]() (10)
(10)
![]()
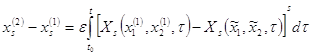
![]()
![]() — удовлетворяет условию Липшица, поэтому мы можем воспользоваться этим, переходя к оценкам
— удовлетворяет условию Липшица, поэтому мы можем воспользоваться этим, переходя к оценкам
![]()
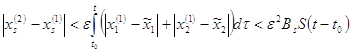 (11)
(11)
![]()
![]()
![]()
![]() (12)
(12)
![]()
Пусть ![]() , причем
, причем ![]() , тогда:
, тогда:
![]() (13)
(13)
Оценим
![]() (14)
(14)
Фактически нужно оценить величину ![]() .
.
![]()
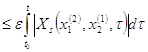
Используем условие Липшица для ![]() , тогда последнее неравенство
, тогда последнее неравенство
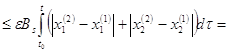
(последняя оценка получена с помощью неравенства (11)).
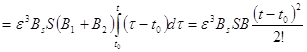 (15)
(15)
![]()
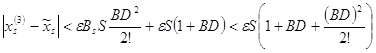 (16)
(16)
Можно увидеть следующую закономерность
![]() (17)
(17)
По методу математической индукции, для ![]() оценки верны. Покажем их справедливость и для
оценки верны. Покажем их справедливость и для ![]()
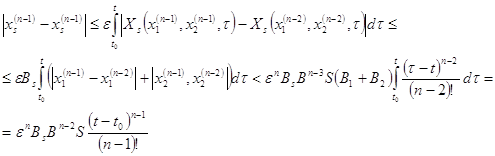
Используя формулу (13), далее получим:
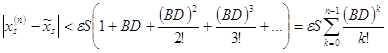 (18)
(18)
Теперь в этом неравенстве перейдем к пределу при ![]()
![]() (19)
(19)
Обозначим через
![]()
Так как мы пользовались условиями Липшица, нужно убедиться, что приближения не выходят из области G.
![]() — по теореме Пикара это не выходит за пределы области G, то есть
— по теореме Пикара это не выходит за пределы области G, то есть
![]()
В силу плотности числовой прямой
![]() , где
, где ![]() (20)
(20)
Проверим, вышло ли первое приближение за пределы области G. Пользуясь оценками (19) и (20), имеем:
![]()
Возьмем
![]() ,
,
тогда
![]()
Аналогично проверяем второе приближение
![]()
Возьмем
![]() , тогда
, тогда
![]()
![]()
И если
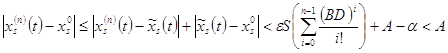 ,
,
если
![]()
Если мы перейдем к перейдем к пределу при ![]() , то получим:
, то получим:
![]() (21)
(21)
Если мы ![]() будем выбирать из условия (21), то использование условия Липшица законно.
будем выбирать из условия (21), то использование условия Липшица законно.
![]() необходимо согласовывать с
необходимо согласовывать с ![]() с помощью (21) и
с помощью (21) и
![]()
Решение уравнения
Рассмотрим уравнение
![]() (1)
(1)
Данное уравнение второго порядка описывает колебательное движение. Здесь ω – некоторая действительная постоянная, а ε – малый параметр.
Делаем в уравнении (1) замену: ![]() тогда получим систему
тогда получим систему
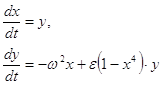 (2)
(2)
![]() (3)
(3)
Далее, дифференцируем (3) по t, считая ![]() и φ
и φ![]() .
.
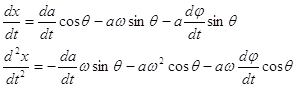 (4)
(4)
Подставим (4) в (2), учитывая (3).
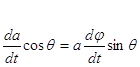
![]() (5)
(5)
Разрешим эту систему относительно ![]()
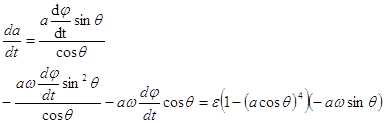
Домножим второе уравнение на ![]()
![]()
![]()
![]() ,
,
тогда имеем:
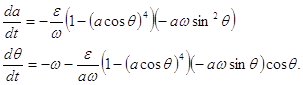 (6)
(6)
Система (6) полностью эквивалентна уравнению (1). Соответствующая системе (6) усредненная система имеет вид
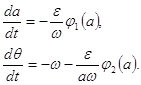 (7)
(7)
В системе (7) ![]() и
и ![]() имеют вид:
имеют вид:
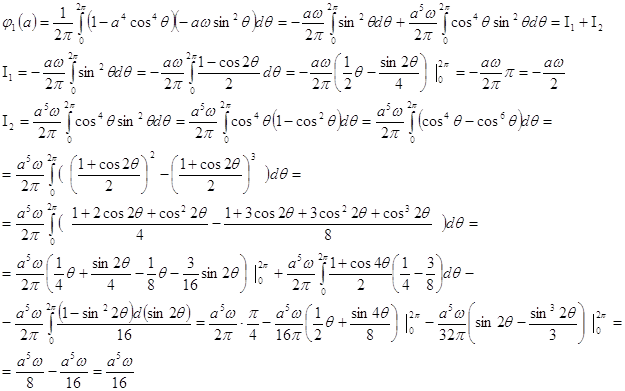
то есть
![]()
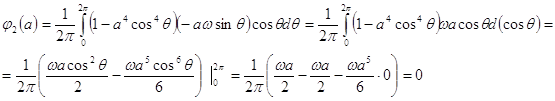
![]()
Таким образом имеем
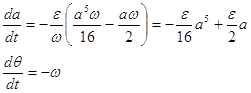 или
или
![]()
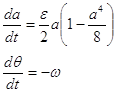 (8)
(8)
Чтобы найти в явном виде закон изменения амплитуды в зависимости от времени, необходимо решить первое уравнение системы (8):
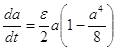
Умножим обе части равенства на ![]() :
:
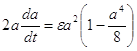 .
.
Сделаем замену
![]()
![]()
![]()
![]() ,
,
умножаем обе части равенства на ![]() :
:
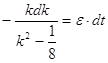
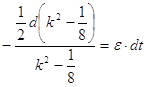
![]()
Так как ![]() ,
,
то тогда ![]() ,
,
или ![]()
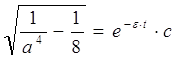
![]()
![]()
Предположим, что ![]() , тогда
, тогда 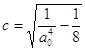
![]()
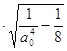 ;
; 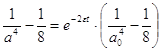 ;
;
![]()
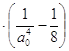 +
+![]() .
.
Отсюда находим
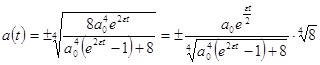 (9а)
(9а)
Колебания представятся следующим образом (находим выражение для приближенного значения x в явном виде)
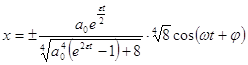 (9)
(9)
Найдем 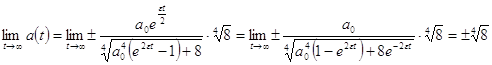
Динамический режим обладает сильной устойчивостью, заключающейся в том, что каково бы ни было значение ![]() , малое или большое, все равно
, малое или большое, все равно ![]() при
при ![]() .
.
Как видно из выражения (9), если начальное значение амплитуды ![]() =0, амплитуда останется равной нулю для любого t, и, следовательно, получим х=0, то есть тривиальное решение уравнения (1). Это тривиальное решение, очевидно, соответствует статическому режиму, то есть отсутствию колебаний в системе.
=0, амплитуда останется равной нулю для любого t, и, следовательно, получим х=0, то есть тривиальное решение уравнения (1). Это тривиальное решение, очевидно, соответствует статическому режиму, то есть отсутствию колебаний в системе.
Однако, исходя из формулы (9), нетрудно заключить, что этот статический режим неустойчив. Действительно, как бы ни было мало начальное значение амплитуды, оно все равно будет монотонно приближаться к значениям, равным ![]() . Таким образом, поскольку случайные малые толчки практически неизбежны, в рассматриваемой колебательной системе, находящейся в состоянии покоя, автоматически возбуждаются колебания с амплитудой, то есть система самовозбуждается.
. Таким образом, поскольку случайные малые толчки практически неизбежны, в рассматриваемой колебательной системе, находящейся в состоянии покоя, автоматически возбуждаются колебания с амплитудой, то есть система самовозбуждается.
Из выражения (9) следует, что если ![]() , то
, то ![]() , и для любых
, и для любых ![]()
![]() очень быстро приближается к значению
очень быстро приближается к значению ![]() независимо от
независимо от ![]() . Это решение соответствует стационарному (установившемуся) динамическому режиму:
. Это решение соответствует стационарному (установившемуся) динамическому режиму:
![]() (10)
(10)
Иначе говоря, любое колебание при увеличении t приближается к стационарному колебанию, то есть колебания будут устойчивы.
Режимы с постоянной амплитудой, для ![]() , приводят к уравнению
, приводят к уравнению
А![]() =
=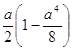 =0
=0
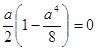 .
.
Корни этого уравнения ![]()
![]() ;
;
![]() ;
; ![]() <0
<0 ![]()
![]()
![]()
Таким образом, ![]() соответствует неустойчивому состоянию равновесия, а
соответствует неустойчивому состоянию равновесия, а ![]() соответствует устойчивому предельному циклу.
соответствует устойчивому предельному циклу.
Для любого заданного положительного сколь угодно малого значения параметра ![]() всегда можно найти такое достаточно малое значение параметра
всегда можно найти такое достаточно малое значение параметра ![]() , для которого уравнение (1) или, что то же самое, система (2), имела бы предельный цикл, лежащий в
, для которого уравнение (1) или, что то же самое, система (2), имела бы предельный цикл, лежащий в ![]() окрестности окружности
окрестности окружности ![]() , причем этот предельный цикл устойчив, если
, причем этот предельный цикл устойчив, если![]() , и неустойчив, если
, и неустойчив, если ![]() . Все эти рассуждения следуют из теоремы Мандельштама и Папалекси.
. Все эти рассуждения следуют из теоремы Мандельштама и Папалекси.
Наряду с точной системой рассматривается приближенная
![]() , (s=1,2) .
, (s=1,2) .
Теорема. Пусть при всех t и в некоторой области переменных ![]() функции
функции ![]() непрерывны и ограничены. Функции
непрерывны и ограничены. Функции ![]() также непрерывны и ограничены в области Г.
также непрерывны и ограничены в области Г. ![]() — 2
— 2![]() -периодические по t. Функции
-периодические по t. Функции ![]() и
и ![]() — удовлетворяют условию Липшица по переменным
— удовлетворяют условию Липшица по переменным ![]() и
и ![]() (при этих условиях существует и единственно решение). Тогда для
(при этих условиях существует и единственно решение). Тогда для![]()
![]() и L>0 :
и L>0 : ![]() , 0
, 0![]() ,
,
где ![]() (s=1,2)
(s=1,2) ![]() =
=![]()
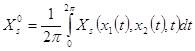
![]() (s=1,2)
(s=1,2)
Проверим выполнение условий теоремы для нашего уравнения. Из системы (6) находим ![]() и
и ![]() :
:
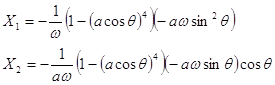
Очевидно, что ![]() и
и ![]() непрерывны.
непрерывны.
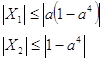 , из этих неравенств видно, что
, из этих неравенств видно, что ![]() и
и ![]() ограничены для любого конечного
ограничены для любого конечного ![]() . Функции
. Функции ![]() и
и ![]() для системы (2) имеют вид:
для системы (2) имеют вид:
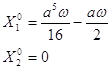 .
.
Из последней системы видно, что ![]() и
и ![]() непрерывны и ограничены для любого конечного
непрерывны и ограничены для любого конечного ![]() .
. ![]() и
и ![]() — периодические по t с любым периодом, в том числе и
— периодические по t с любым периодом, в том числе и ![]() . Функции
. Функции ![]() и
и ![]() ,
, ![]() и
и ![]() непрерывно дифференцируемы по t, а следовательно удовлетворяют условию Липшица.
непрерывно дифференцируемы по t, а следовательно удовлетворяют условию Липшица.
Пусть ![]() и
и ![]() — решения точной системы (6). Тогда для
— решения точной системы (6). Тогда для ![]()
![]() и
и ![]() :
: 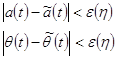 ,
, ![]() .
.
( В нашем случае ![]() ,
, ![]() определяется уравнением (9а)).
определяется уравнением (9а)).
Выводы
В рамках теории Ван-дер-Поля нельзя уточнить полученные решения.
В заключение заметим, что метод Ван-дер-Поля позволил исследовать достаточно широкий круг задач нелинейной механики (с одной степенью свободы), и задач радио- и электротехники, обладает наглядностью и удобен для проведения расчетов. Благодаря этому методу созданы генераторы стационарных колебаний в радиоприемных и радиопередающих устройствах, которые используются и по сей день в современной технике. В рамках теории Ван-дер-Поля нельзя уточнить полученные решения.
Список использованной литературы
1. Ю.А. Митропольский Метод усреднения в нелинейной механике, «Наукова думка» Киев — 1971г.
2. Н.Н. Моисеев Асимптотические методы нелинейной механики, М.: Наука, 1981г.
3. А. Найфэ Методы возмущений. Издательство «Мир», Москва—1976г.
4. А. Найфэ Введение в методы возмущений. «Мир», 1984г.
5. Андронов А.А., Витт А.А., Хайкин С.Э. Теория колебаний. Физматгиз, М.,1959г.
Похожие работы
... о биологической причинности. Ряд феноменов, которые витализм считал специфическими для биологических объектов (способность к саморегуляции, усложнение строения, достижение одного результата разными способами) рассматриваются в современном естествознании как типичные проявления процессов самоорганизации любых достаточно сложных систем, а не только живых. Н.Бор: “ни один результат биологического ...
... цепи W1(s) = Wp(s) представлено как параллельное соединение простейших звеньев. 2.9 Неопределенность моделей систем управления Математические модели не отражают исчерпывающим образом динамические свойства систем управления в силу идеализации и упрощений, неизбежных при моделировании, неточной реализации алгоритмов управления и изменений характеристик объектов и других элементов в ...
... строки. Очевидно, что такая операция не изменит знака членов следующей строки и не отразится на конечном результате. Например, элементы третьей строки таблицы (45) можно было бы разделить на 8 для упрощения последующих вычислений. Анализ результатов устойчивости в нелинейных системах. При исследовании устойчивости в цепях постоянного тока при малых возмущениях обнаружение неустойчивости ...
... потенциал ионизации. 4.3 Методика экспериментальных исследований Основной целью проведенных экспериментов было исследование влияния лазерного излучения на электропроводность диэлектрических жидкостей и изучение практической возможности реализации электроэрозионных явлений в диэлектрической среде. Эксперименты проводятся для исследования влияния следующих параметров: · ...

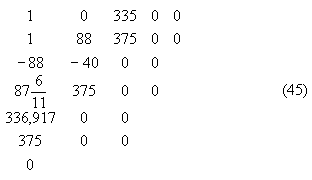
0 комментариев