Навигация
Формула трапеций и средних прямоугольников
10801
знак
2
таблицы
4
изображения
1.3 Формула трапеций и средних прямоугольников.
Заменим дугу АВ стягивающей ее хордой, получим прямолинейную трапецию аАВb, площадь которой примем за приближенное значение интеграла
B
y
A
0 a b x
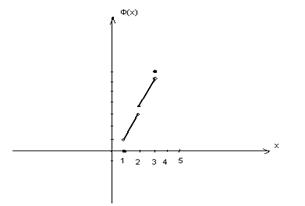
рис 1.3.1 Криволинейная трапеция
Рис. 1.3.2. Метод трапеций.
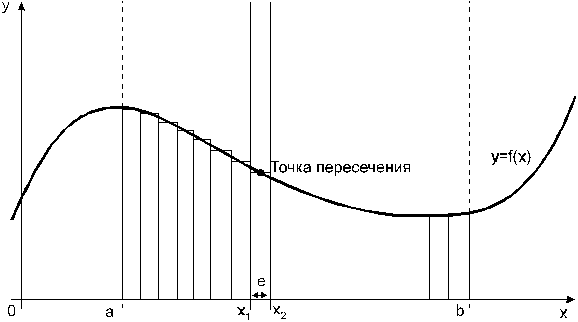
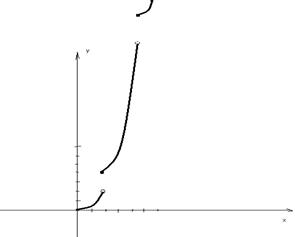
Рис. 1.3.3. Метод средних прямоугольников.
По методам трапеций и средних прямоугольников соответственно интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо малая величина (точность), и сумма площадей прямоугольников, где основание прямоугольника какая-либо малая величина (точность), а высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать в середине. Соответственно получаем формулы площадей —
для метода трапеций:
,
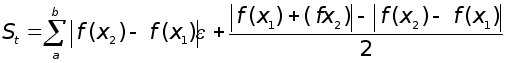для метода средних прямоугольников:
.
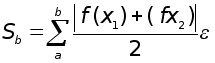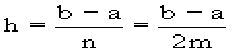Применив
формулу Симпсона
к каждому удвоенному
промежутку
[x0,x2], [x2,x4] ... [x2m-2,x2m] длины
2h и введя обозначения 1=y1+y2+
... +y2m-1 2=y2+y4+
... +y2m получим
обобщенную
формулу Симпсона: 
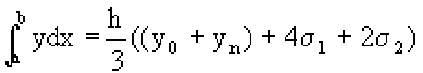Остаточный
член формулы
Симпсона в
общем виде:
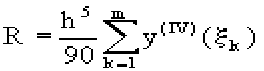где k I (x2к-2,x2к)1.5. Квадратурная формула Чебышева
Рассмотрим квадратурную формулу вида:
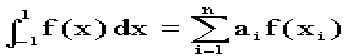
функцию f(x) будем исать в виде когда f(x) многочлен вида f(x)=ao+a1x+...+anxn . Проинтегрировав, преобразовав и подставив значения многочлена в узлах
f(x1)=a0+a1x1+a2x12+a3x13+...+anx1n
f(x2)=a0+a1x2+a2x22+a3x23+...+anx2n
f(x3)=a0+a1x3+a2x32+a3x33+...+anx3n
. . . . . . . . . . . . . . . .
f(xn)=a0+a1xn+a2xn2+a3xn3+...+anxnn
получим формулу Чебышева.
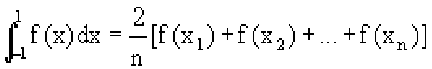
Значения х1,х2,..,хn для различных n приведены в таблице 3.
Таблица 3 – Значения х1,х2,..,хn для различных n.
| n | I | ti | n | i | ti |
| 2 | 1;2 | 0,577350 | 6 | 1;6 | 0,866247 |
| 3 | 1;3 | 0,707107 | 2;5 | 0,422519 | |
| 2 | 0 | 3;4 | 0,266635 | ||
| 4 | 1;4 | 0,794654 | 7 | 1;7 | 0,883862 |
| 2;3 | 0,187592 | 2;6 | 0,529657 | ||
| 5 | 1;5 | 0,832498 | 3;5 | 0,321912 | |
| 2;4 | 0,374541 | 4 | 0 | ||
| 3 | 0 |
Похожие работы
... for i: = n-1 to n do; c[i]: = 1 - c[n+1-i]; end; {заполнение y-ков в массиве у[5]} procedure form(var x:aa; var y:aa); var i:integer; Begin for i:=1 to n do y[i]:=sin(x[i]); {функция} end; {процедура для расчета интеграла по квадратурной формуле Чебышева} procedure cheb(var y:aa;var ich:real); var i:integer; Begin ich: = 0; for i: = 1 to n do ich: = ich+y[i]*h; end; {процедура вывода таблицы} ...
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
-6 S3 = 1.58075·10-5 Задача 2 Для функции g(x), заданной своими значениями в шести точках, составить таблицу всех повторных разностей. Преобразовать функцию g(x) с помощью линейного преобразования x = a + b * k в функцию G(k) с целочисленным аргументом k. В качестве проверки правильности заполнения таблицы вычислить аналитически конечную разность Δng(x) = ΔnG(k) для n = 5. ...
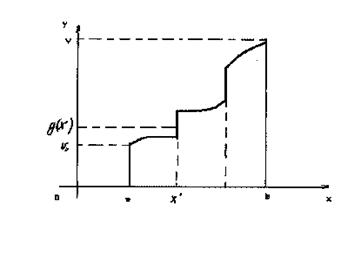
... 2.6 Приведение интеграла Стилтьеса к интегралу Римана Пусть функция непрерывна в промежутке , а монотонно возрастает в этом промежутке, и притом в строгом смысле. Тогда, как показал Лебег, интеграл Стилтьеса с помощью подстановки непосредственно приводится к интегралу Римана. На рисунке изображен график функции . Для тех значений , при которых функция испытывает скачок (ибо мы вовсе ...
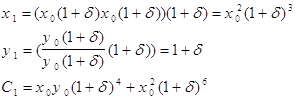
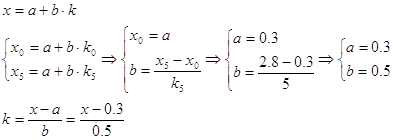
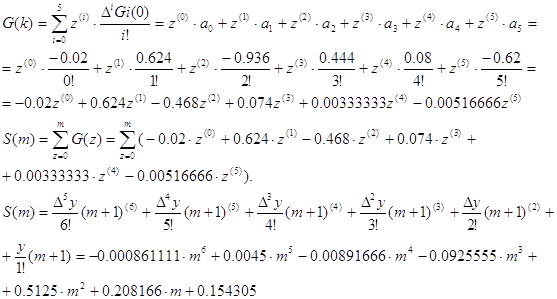
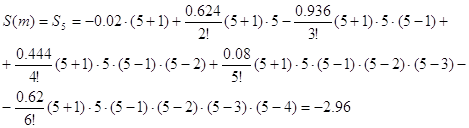
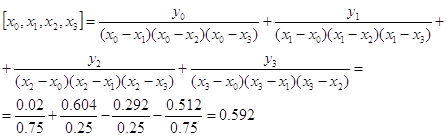
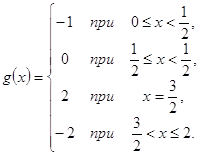
0 комментариев