Навигация
Решение контрольного примера
2. Решение контрольного примера
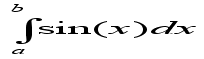
где a=0 ; b= ![]() ; при n=5;
; при n=5;
f(x) = sin(x);
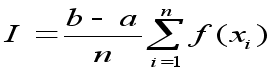
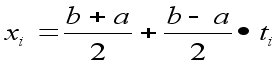
| i | xi | yi |
| 1 | 0,131489 | 0,131118 |
| 2 | 0,490985 | 0,471494 |
| 3 | 0,785 | 0,706825 |
| 4 | 0,509015 | 0,487317 |
| 5 | 0,868511 | 0,763367 |
x1= /4+/4*t1=/4+/4(-0,832498)=0,131489
x2= /4+/4*t2=/4+/4(-0,374341)=0,490985
x3= /4+/4*t3=/4+/4*0=0,785
x4=1- x2=1-0,490985 = 0,509015
x5=1- x1=1-0,131489=0,868511
y1=sin(x1) = sin(0,131489)=0,131118y2=sin(x2) = sin(0,490985)=0,471494
y3=sin(x3) = sin(0,785)=0,706825
y4=sin(x4) = sin(0,509015)=0,487317
y5=sin(x5) = sin(0,868511)=0,763367
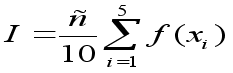
I = /10(0,131118+0,471494+0,706825+0,487317+0,763367) =
=/10*2,560121=0,8038779.
3. Описание программы Integral. pas. Алгоритм.
Процедура VVOD - заполняет массив, содержащий в себе аргументы xi
Процедура FORM - используя массив, содержащий аргументы xi заполняет массив yiПроцедура CHEB - используя массивы xi и yi, высчитывает по квадратурной формуле Чебышева приближенное значение интеграла.
Процедура TABL - это подпрограмма, осуществляющая вывод таблицы узлов (аргумент - функция)
При запуске программы нужно ввести границы интегрирования.
После ввода границ интегрирования используется процедура VVOD, а затем высчитывается и выводиться на экран шаг табулирования функции h.
После этого используем процедуры FORM и CHEB .
Получив результат, выводим таблицу ( процедура TABL ) и интеграл.
4. Заключение и выводы.
Таким образом очевидно, что при вычислении определенных интегралов с помощью квадратурных формул, а в частности по формуле Чебышева не дает нам точного значения, а только приближенное.
Чтобы максимально приблизиться к достоверному значению интеграла нужно уметь правильно выбрать метод и формулу, по которой будет вестись расчет. Так же очень важно то, какой будет взят шаг интегрирования.
Хотя численные методы и не дают очень точного значения интеграла, но они очень важны, так как не всегда можно решить задачу интегрирования аналитическим способом.
5.Список литературы:
1. Ракитин Т.А., Первушин В.А. “Практическое руководство по численным методам с приложением программ на языке Basic“ 2. Крылов В.И. “Приближенные вычисления интегралов“ - М. : Физмат. 3. Демидович и Марон “Основы вычислительной математики“ 4. Копченова и Марон “Вычислительная математика в примерах и задачах”5. Вольвачев А.Н., Крисевич В.С. Программирование на языке Паскаль для ПЭВМ ЕС. Минск.: 1989 г.
6. Зуев Е.А. Язык программирования Turbo Pascal. М.1992 г.
7. Скляров В.А. Знакомьтесь: Паскаль. М. 1988 г.
6. Листинг программы.Программа написана на языке Tubro Pascal 7.0 для MS-DOS. Ниже приведен ее листинг:
program integral;
uses crt;
const n=5;
k=-0.832498;
l=-0.374541;
z=0.0;
type aa=array[1..n] of real;
var x,y:aa;
a,b,h,ich:real;
{ заполнение х-сов в массив х[5] }
procedure vvod(var a,b:real;var c:aa);
var i:integer;
t:aa;
Begin
t[1]:=k;
t[2]:=l;
t[3]:=z;
t[4]:=l;
t[5]:=k;
for i:=1 to n-1 do
c[i]:=((b+a)/2+(b-a)/2*t[i]);
for i:=n-1 to n do
c[i]:=1 - c[n+1-i];
end;
{ заполнение y-ков в массиве у[5] }
procedure form(var x:aa; var y:aa);
var i:integer;
Begin
for i:=1 to n do
y[i]:=sin(x[i]); {функция}
end;
{ процедура для расчета интеграла по квадратурной
формуле Чебышева }
procedure cheb(var y:aa;var ich:real);
var i:integer;
Begin
ich:=0;
for i:=1 to n do
ich:=ich+y[i]*h;
end;
{ процедура вывода таблицы}
procedure tabl;
var i:integer;
Begin
writeln(' ___________________________________ ');
writeln('| i | t | x | y |');
writeln(' ___________________________________ ');
writeln('| 1 |',k:9:6,'|',x[1]:9:6,' |',y[1]:9:6,'|');
writeln('| 2 |',l:9:6,'|',x[2]:9:6,' |',y[2]:9:6,'|');
writeln('| 3 |',z:9:6,'|',x[3]:9:6,' |',y[3]:9:6,'|');
writeln('| 4 |',l:9:6,'|',x[4]:9:6,' |',y[4]:9:6,'|');
writeln('| 5 |',k:9:6,'|',x[5]:9:6,' |',y[5]:9:6,'|');
writeln(' ___________________________________ ');
end;
Begin
clrscr;
writeln(' П Р О Г Р А М М А Д Л Я В Ы Ч И С Л Е Н И Я');
writeln(' О П Р Е Д Е Л Е Н Н О Г О И Н Т Е Г Р А Л А ');
writeln;
writeln('Введите границы интегрирования a,b:');
readln(a,b);
vvod(a,b,x);
h:=(b-a)/n;
writeln('h=',h:9:6);
form(x,y);
cheb(y,ich);
tabl;
writeln('I=',ich:8:6);
end.
Вывод результата :
П Р О Г Р А М М А Д Л Я В Ы Ч И С Л Е Н И Я
О П Р Е Д Е Л Е Н Н О Г О И Н Т Е Г Р А Л А
Введите границы интегрирования a,b:
0 1.5708
h= 0.314160
____________________________
| i | t | x | y |
____________________________
| 1 |-0.832498| 0.131556 | 0.131177|
| 2 |-0.374541| 0.491235 | 0.471716|
| 3 | 0.000000| 0.785400 | 0.707108|
| 4 |-0.374541| 0.508765 | 0.487099|
| 5 |-0.832498| 0.868444 | 0.763325|
____________________________
I=0.8043
Похожие работы
... for i: = n-1 to n do; c[i]: = 1 - c[n+1-i]; end; {заполнение y-ков в массиве у[5]} procedure form(var x:aa; var y:aa); var i:integer; Begin for i:=1 to n do y[i]:=sin(x[i]); {функция} end; {процедура для расчета интеграла по квадратурной формуле Чебышева} procedure cheb(var y:aa;var ich:real); var i:integer; Begin ich: = 0; for i: = 1 to n do ich: = ich+y[i]*h; end; {процедура вывода таблицы} ...
... с помощью рекурентных соотношений? 104) Приведите конечно-разностные выражения для первой производной. 105) Подынтегральная функция y = f(x) задана таблицейВзяв h = 0,3, вычислить интеграл на отрезке [0,3; 0,9] методом Симпсона. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету ЧИСЛЕННЫЕ МЕТОДЫ Билет № 22 106) Как ...
-6 S3 = 1.58075·10-5 Задача 2 Для функции g(x), заданной своими значениями в шести точках, составить таблицу всех повторных разностей. Преобразовать функцию g(x) с помощью линейного преобразования x = a + b * k в функцию G(k) с целочисленным аргументом k. В качестве проверки правильности заполнения таблицы вычислить аналитически конечную разность Δng(x) = ΔnG(k) для n = 5. ...
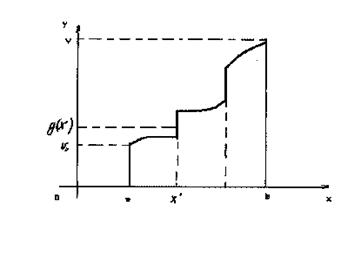
... 2.6 Приведение интеграла Стилтьеса к интегралу Римана Пусть функция непрерывна в промежутке , а монотонно возрастает в этом промежутке, и притом в строгом смысле. Тогда, как показал Лебег, интеграл Стилтьеса с помощью подстановки непосредственно приводится к интегралу Римана. На рисунке изображен график функции . Для тех значений , при которых функция испытывает скачок (ибо мы вовсе ...
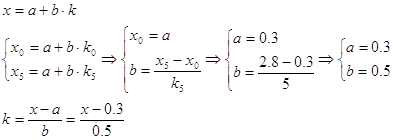
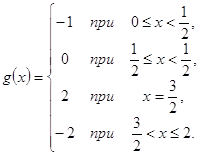
0 комментариев