Выполнили: Мамедалиева Ирада и
Павлова Галина
ученицы 11"А" класса
средней школы №36
Научный руководитель:
учитель математики
средней школы № 36
Крайняя В.В..
Норильск 2000 г.
Содержание.
Введение.
Приближённое решение уравнений :
2.1 Способ хорд (или способ линейной интерполяции).
Способ касательных (или способ Ньютона).
Комбинированный способ (комбинированное применение способов хорд и касательных).
Заключение.
Список литературы.
Приложение :
а) рисунок № 1
б) рисунок № 2
в) рисунок № 3
г) рисунок № 4
д) рисунок № 5
е) рисунок № 6
ж) рисунок № 7
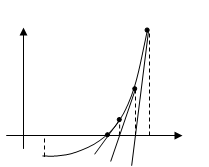
Приближённое решение уравнений. Если квадратные уравнения решали уже древние греки, то способы решения алгебраических уравнений третьей и четвёртой степени были открыты лишь в XVI веке. Эти классические способы дают точные значения корней и выражают их через коэффициенты уравнения при помощи радикалов различных степеней. Однако эти способы приводят к громоздким вычислениям и поэтому имеют малую практическую ценность. В отношении алгебраических уравнений пятой и высших степеней доказано, что в общем случае их решения не выражаются через коэффициенты при помощи радикалов. Не выражаются в радикалах, например, корни уже такого простого по виду уравнения, как: х^5-4х-2=0 Сказанное, однако, не означает отсутствия в науке методов решения уравнения высших степеней. Имеется много способов приближенного решения уравнений - алгебраических и неалгебраических (или, как их называют, трансцендентных), позволяющих вычислять их корни с любой, заранее заданной степенью точности, что для практических целей вполне достаточно. На простейших из таких способов мы и остановимся, причём речь будет идти о вычислении действительных корней. Пусть нужно решить уравнение: f(x)=0 (1) Если обратиться к рисунку, то каждый корень уравнения (1) представляет собой абсциссу точки пересечения графика функции y=f(х)C осью Ох (рисунок №1)
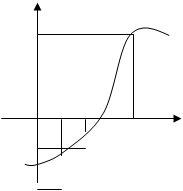
С помощью графика функции или каким-нибудь иным способом обычно удаётся установить приблизительные значения корней. Это позволяет для каждого корня получить грубые приближения по недостатку и по избытку. Такого рода грубых приближений во многих случаях оказывается достаточно, чтобы, отправляясь от них, получить все значения корня с требуемой точностью. Об этом и пойдёт речь.
Итак, пусть корень Е уравнения (1) "зажат" между двумя его приближениями а и b по недостатку и по избытку а< E0, f``(х)>0 (рисунок №3), - в остальных случаях рассуждение вполне аналогично. В этом первом случае x1 лежит между a и Е. С отрезком [x1, b] поступаем так же, как мы поступаем с отрезком [a, b] (рисунок №4). При этом для нового приближённого значения корня получаем: x1 = x2-(b- x1)*f(x1)/f(b)-f(x1) ( в формуле (2) заменяем x1 на x2, а на x1 ); значение x2 оказывается между x1 и Е. Рассматриваем отрезок [x2, b] и находим новое приближённое x3, заключённое между x2 и Е и. т. д. В результате получим последовательность а
Похожие работы
... уравнения являются нули соответствующей функции. Следует отметить, что обе функции непрерывны и дважды дифференцируемы на всей области определения (–¥ ; ¥). Необходимо найти приближенные решения уравнений с заданной точностью (0,001). С целью упростить работу (в частности, избавить человека от однотипных арифметических и логических операций) и обеспечить максимальную точность ...
... . Ван-дер-Поль показал, что для этой цели можно использовать малые нелинейности, однако даже при малых нелинейностях получившаяся задача не допускала интегрирования колебаний в квадратурах. Ван-дер-Поль разработал приближенный асимптотический метод интегрирования дифференциальных уравнений второго порядка подобного рода. 1.1. Метод усреднения Ван-дер-Поля. В своих исследованиях Ван-дер-Поль ...
... . Уравнение (2; 0,1) с оператором А, обладающим указанными свойствами, будем называть операторным уравнением первого рода, или, короче,— уравнением первого рода. 2.1. Метод подбора решения некорректно поставленных задач 2.1.1. Широко распространенным в вычислительной практике способом приближенного решения уравнения (2; 0,1) является метод подбора. Он состоит в том, что для элементов z ...
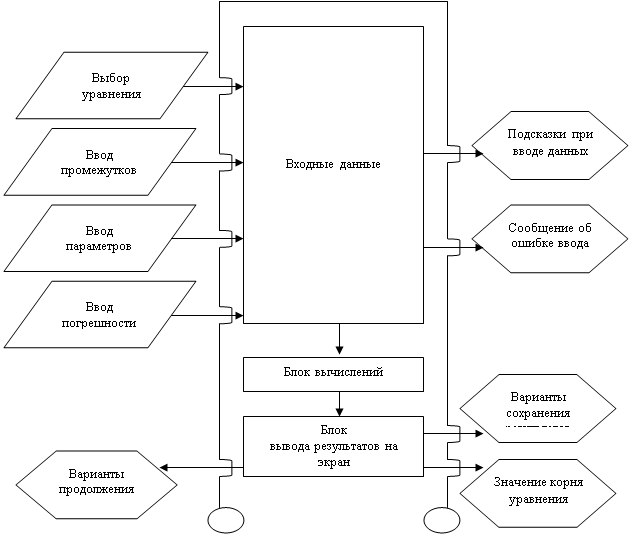
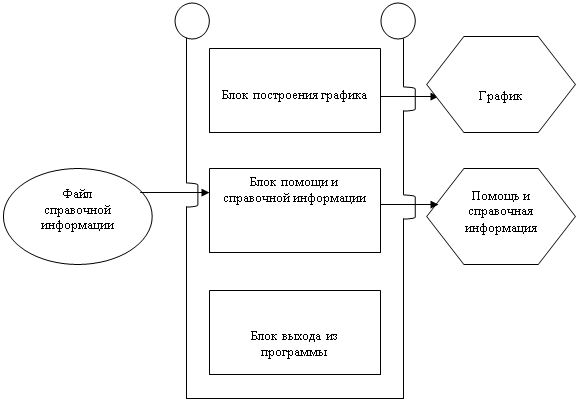
... от 23.02. 2004 г. – Донецк: ДонГИИИ, 2004, 46 с. Приложение А ТЕХНИЧЕСКОЕ ЗАДАНИЕ А.1 Общие сведения Полное название программного продукта: "Численные методы. Решение уравнений с одной переменной методом Ньютона (касательных)". Её условное обозначение РУОП. Работа выполняется студентом 1-го курса Донецкого государственного института искусственного интеллекта (ДонГИИИ), факультета СКИТ, ...



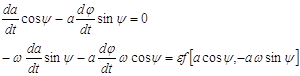
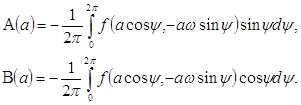
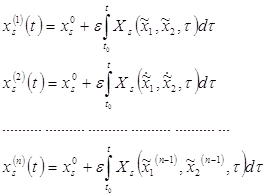
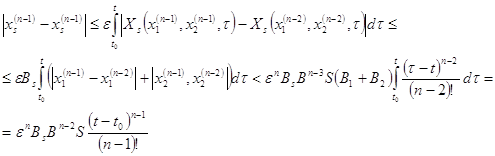

0 комментариев