Навигация
Производная и ее применение в экономической теории
Министерство образования и науки Украины
Донецкий национальный технический университет
РЕФЕРАТ
по высшей математике
на тему:
«Производная и ее применение в экономической теории»
Донецк – 2008
Вступление
Современный экономист должен хорошо владеть количественными методами анализа. К такому выводу нетрудно прийти практически с самого начала изучения экономической теории. При этом важны как знания традиционных математических курсов (математический анализ, линейная алгебра, теория вероятностей), так и знания, необходимые непосредственно в практической экономике и экономических исследованиях (математическая и экономическая статистика, теория игр, эконометрика и др.).
Математика является не только орудием количественного расчета, но также методом точного исследования. Она служит средством предельно четкой и ясной формулировки экономических понятий и проблем.
Ф.Энгельс в своё время заметил, что "лишь дифференциальное исчисление даёт естествознанию возможность изображать математически не только состояния, но и процессы: движение". Поэтому целью моей работы является выяснить, каков экономический смысл производной, какие новые возможности для экономических исследований открывает дифференциальное исчисление, а также исследовать применение производной при решении различных видов задач по экономической теории.
1. Определение производной
Пусть функция y=f(х) определена в некоторой окрестности точки х0. Для любой точки х из этой окрестности приращение Dx определяется формулой Dx=х – х0, откуда х=х0+Dx.
Приращением функции y=f(x) в точке х0 называется разность
Dу=f(x) – f(x0)=f(x0+Dx) – f(x0).
Производной от функции у=f(x) в точке х0 называется предел отношения приращения функции к приращению аргумента (![]() ), когда приращение аргумента стремится к нулю (Dx→0).
), когда приращение аргумента стремится к нулю (Dx→0).
Производная функции у=f(x) в точке х0 обозначается y'(х0) или f'(х0). Определение производной можно записать в виде формулы:
![]() '(
'(![]() )=
)=![]()
![]() =
= ![]()
![]() .
.
Если функция в точке х0 имеет конечную производную, то она называется дифференцируемой в точке х0. Если она дифференцируема во всех точках промежутка X, то говорят, она дифференцируема на всём этом промежутке.
Конечно, ![]()
![]() может не существовать. В этом случае говорят, что функция f(x) не имеет производной в точке х0. Если
может не существовать. В этом случае говорят, что функция f(x) не имеет производной в точке х0. Если ![]()
![]() равен
равен ![]() или
или ![]() , то говорят, что функция f(x) имеет в точке х0 бесконечную производную (равную
, то говорят, что функция f(x) имеет в точке х0 бесконечную производную (равную ![]() или
или ![]() , соответственно).
, соответственно).
1.1 Геометрический смысл понятия производной
Пусть на плоскости x0y дана непрерывная кривая y=f(x)(см. рис. 1).
Рассмотрим на графике кривой точки Mo(xo;f(xo)) и M1(xo+Dx; f(xo+Dx)). Проведем секущую MoM1. Пусть ![]() – угол наклона секущей MoM1 относительно оси 0х. Если существует предел
– угол наклона секущей MoM1 относительно оси 0х. Если существует предел ![]() , то прямая, проходящая через Mo и образующая с осью 0х угол
, то прямая, проходящая через Mo и образующая с осью 0х угол ![]() , называется касательной к графику данной кривой в точке Mo. Таким образом, под касательной к кривой y=f(х) в точке Mo естественно понимать предельное положение секущей MoM1, к которому она стремится, когда Dx®0.
, называется касательной к графику данной кривой в точке Mo. Таким образом, под касательной к кривой y=f(х) в точке Mo естественно понимать предельное положение секущей MoM1, к которому она стремится, когда Dx®0.
Пусть N(xo+Dx; f(xo)) – точка, дополняющая отрезок MoM1 до прямоугольного треугольника MoM1N. Так как сторона MoN параллельна оси 0х, то
![]()
Переходя к пределу в левой и правой частях этого равенства при Dx→0, получим
![]()
Поэтому геометрический смысл производной состоит в том, что f’(x0) – это тангенс угла наклона (угловой коэффициент) касательной к графику y=f(х) в точке (xo; f(xo)).
Найдём уравнение касательной к графику в точке Mo(xo; f(xo)) в виде y=kx+b. Так как Mo![]() f(x), то должно выполняться равенство f(x0)=kx0+b, откуда b= f(x0) – kx0. Следовательно, касательная задаётся уравнением
f(x), то должно выполняться равенство f(x0)=kx0+b, откуда b= f(x0) – kx0. Следовательно, касательная задаётся уравнением
y=kx+f(x0) – kx0=f(x0)+k(x – x0).
Поскольку k=f'(x0), то уравнение касательной имеет вид
y=f(x0)+f'(x0)(x – x0).
Как вычисляют производную?
Похожие работы
... ). Мы придерживаемся точки зрения, согласно которой региональная экономика является ветвью общей экономической теории, относящейся к разделу «Мезоэкономика», то есть рассматриваем региональную экономику как часть крупную подсистему национальной экономики (Макроэкономики). Курс методологически опирается на основы экономической теории и органически связан с конкретными экономическими дисциплинами, ...
... их изменения, аналитическим выражением которых являются производные. Такие уравнения, содержащие производные, называются дифференциальными. В своей же работе я хочу подробнее остановится на приложениях производной. 1. Понятие производной При решении различных задач геометрии, механики, физики и других отраслей знания возникла необходимость с помощью одного и того же аналитического процесса из ...
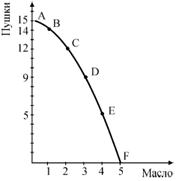
... , дополнительная отдача будет постоянной. Рента с лучших земель останется на том же уровне R1. 20. Макроэкономика и ее цели. Основные субъекты макроэкономики Макроэкономика – часть экономической теории, изучающая закономерности функционирования и тенденции развития экономики страны в целом. Объект исследования макроэкономики – целостная национальная экономика. Цели макроэкономики: · ...
... бюджета. Исходным теоретическим основанием финансовой политики выступает фискальная политика, как совокупность мер по сознательному манипулированию налогами и государственными расходами. В современной экономической теории существуют различные точки зрения на методы проведения фискальной политики государства. Сторонники кейнсианского направления традиционно ориентируются на создание ...

0 комментариев