Навигация
< c1 Ј k(x, t) Ј c2, r (x, t) і c3 > 0.(22)
0 < c1 Ј k(x, t) Ј c2, r (x, t) і c3 > 0.(22)
![]()
Дифференциальное выражениепри каждом
фиксированном t аппроксимируем в точке (xi, t) так же, как и в стационарном случае, разностным отношением
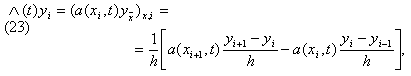
где разностный коэффициент теплопроводности a(xi, t) должен удовлетворять условиям второго порядка аппроксимации
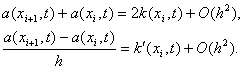
Наиболее употребительны следующие выражения для a(xi, t):
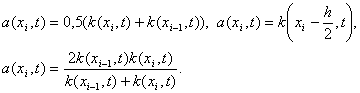
Разностная схема с весами для задачи (21) имеет вид
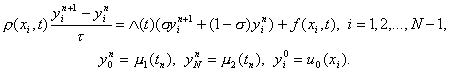 (24)
(24)
Здесь в качестве t можно взять любое значение t О [tn, tn+1], например t = tn + 0,5t . Если в уравнении (24) t = tn + 0,5t , s = 0,5, то схема (24) имеет второй порядок аппроксимации по t и по h. При остальных значениях s и t выполняется первый порядок аппроксимации по t и второй – по h.
При исследовании устойчивости разностных схем с переменными коэффициентами иногда применяется принцип замороженных коэффициентов, сводящий задачу к уравнению с постоянными коэффициентами. Рассмотрим явную схему, соответствующую уравнению (24) с s = 0 и f(xi, t) є 0, т.е. схему
![]() (25)
(25)
Предположим, что коэффициенты r (xi, t), a(xi, t) – постоянные, r (xi, t) є r = const, a(xi, t) є a = const. Тогда уравнение (25) можно записать в виде
![]()
![]() или
или
Из п.2 известно, что последнее уравнение устойчиво при t ’ Ј 0,5h2, т.е. при
![]() (26)
(26)
Принцип замороженных коэффициентов утверждает, что схема (25) устойчива, если условие (26) выполнено при всех допустимых значениях a(xi, t), r (xi, t), т.е. если при всех x, t выполнены неравенства
![]() (27)
(27)
Если известно, что 0 < c1 Ј a(xi, t) Ј c2, r (xi, t) і c3 > 0, то неравенство (27) будет выполнено при
![]()
Строгое обоснование устойчивости схемы (25) будет дано в примере 2 из главы 2.
Если параметр s і 0,5, то из принципа замороженных коэффициентов следует абсолютная устойчивость схемы (24).
Рассмотрим теперь первую краевую задачу для нелинейного уравнения теплопроводности
![]() (28)
(28)
В случае нелинейных уравнений, когда заранее неизвестны пределы изменения функции k(u), избегают пользоваться явными схемами. Чисто неявная схема, линейная относительно yin+2, i = 1, 2,…, N – 1, имеет вид
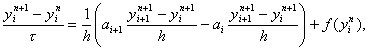 (29)
(29)
где ai = 0,5 (k(yni) + k(yni-1)). Эта схема абсолютно устойчива, имеет первый порядок аппроксимации по t и второй – по h. Решение yin+1, i = 1, 2,…, N – 1, находится методом прогонки. Заметим, что схему (29) можно записать в виде
![]()
где ki = k(yin).
Часто используется нелинейная схема
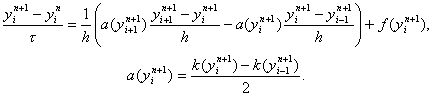 (30)
(30)
Для реализации этой схемы необходимо применить тот или иной итерационный метод. Например такой:
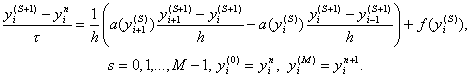 (31)
(31)
Здесь s – номер итерации. Как видим, нелинейные коэффициенты берутся с предыдущей итерации, а в качестве начального приближения для yin+1 выбирается yin. Это начальное приближение тем лучше, чем меньше шаг t . Число итераций M задается из соображений точности. В задачах с гладкими коэффициентами при k(u) і c1 > 0 часто бывает достаточно провести две – три итерации. Значения yi(S+1) на новой итерации находятся из системы (31) методом прогонки. При M = 1 итерационный метод (31) совпадает с разностной схемой (29).
Для приближенного решения нелинейного уравнения (28) применяются также схемы предиктор – корректор второго порядка точности, аналогичные методу Рунге – Кутта для обыкновенных дифференциальных уравнений. Здесь переход со слоя n на слой n+1 осуществляется в два этапа. Приведем пример такой схемы. На первом этапе решается неявная линейная система уравнений
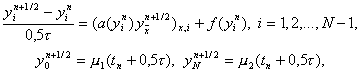
из которой находятся промежуточные значения yin+1/2, i = 0, 1,…, N. Затем на втором этапе используется симметричная шеститочечная схема для уравнения (28), в которой нелинейные коэффициенты a(y), f(y) вычисляются при y = yin+1/2, т.е. схема
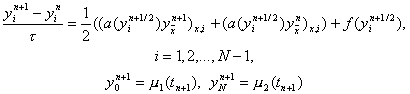
Похожие работы
... пропорциональной второй степени h: Подстановка таких начальных условий в решение сохранит погрешность результатов на уровне . В таком случае говорят, что разностная схема имеет второй порядок точности. 3. Разностные системы уравнений для краевых задач Исходные дифференциальные уравнения во многих физических и технических применениях решаются для случаев, когда заданы значения искомых ...
... схема со сглаживанием, схема прямоугольник со сглаживанием, “шахматная ” схема. Произведены некоторые расчеты для одномерного уравнения переноса с переменными и постоянными коэффициентами на неравномерных сетках, с целью определения наиболее устойчивой разностной схемы. Исследование показало, что наиболее устойчивым методом для одномерного уравнения переноса с переменными коэффициентами является ...
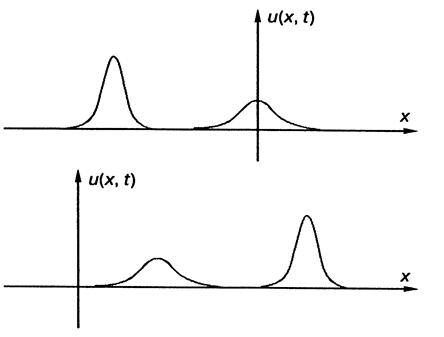
... эксперименты по моделированию распространения таких волн, Крускал и Забуски рассмотрели их столкновение. Остановимся подробнее на обсуждении этого замечательного факта. Пусть имеются две уединенные волны, описываемые уравнением Кортевега—де Фриса, которые различаются амплитудами и движутся друг за другом в одном направлении (рис. 2). Из формулы для уединенных волн (8) следует, что скорость ...
... суммы и позволит вычислить приближенное значение приращения Dy: где Метод четвертого порядка для q = 3, имеет вид где Особо широко известно другое вычислительное правило Рунге-Кутта четвертого порядка точности: где Метод Рунге-Кутта имеет погрешность четвертого порядка (~ h4 ). Правило Рунге. Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно ...
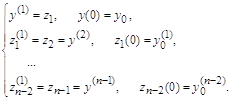
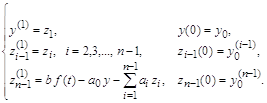
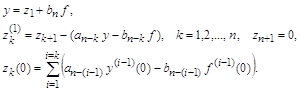
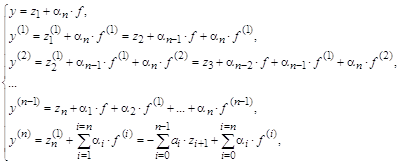
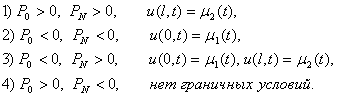



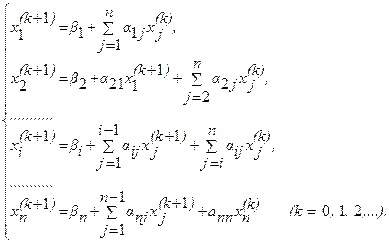
0 комментариев