Навигация
Краевые задачи и разностные схемы
26705
знаков
20
таблиц
17
изображений
Реферат з курсу “Введение в численные методы”
Тема: “КРАЕВЫЕ ЗАДАЧИ И РАЗНОСТНЫЕ СХЕМЫ”
Содержание
1. Приведение к системе уравнений первого порядка
2. Разностное представление систем дифференциальных уравнений
3. Разностные системы уравнений для краевых задач
4. Краевые задачи второго порядка
5. Разностные схемы для уравнений в частных производных
6. Повышение точности разностных схем
7. Сеточные методы для нестационарных задач
Литература
1. Приведение к системе уравнений первого порядка
Для решения систем дифференциальных уравнений высокого порядка методами конечных разностей в первую очередь возникает потребность преобразования исходной системы в систему дифференциальных уравнений первого порядка с соответствующим образом преобразованными начальными или граничными условиями. И уже далее реализовывать численную процедуру решения.
Преобразование в систему уравнений первого порядка не единственно. Наиболее популярные из них в большинстве своем касаются линейных систем с постоянными или переменными коэффициентами. Основная идея всех методов состоит во введении новых переменных и выполнении замены высших производных этими переменными.
Пусть неоднородное дифференциальное уравнение высокого порядка задано в виде:
где 
– соответственно i-тая производная искомого решения и ее значение в начальный момент,
– функция, описывающая внешнее воздействие на динамический объект.
Обозначим первую производную искомой функции новой переменной 
, первую производную – следующей переменной: 
, первую производную – переменной 
и т.д.. Таким образом из исходной системы мы сформируем 
дифференциальное уравнение первого порядка:
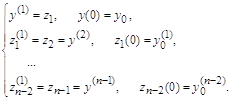
При таких заменах производных искомой функции 
ее n-ная производная оказывается равной первой производной от 
:
В результате, эквивалентная система дифференциальных уравнений первого порядка примет следующий вид:
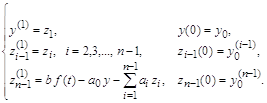
В случае, когда правая часть представлена взвешенной суммой функции 
и ее производных и в целом дифференциальное уравнение имеет вид
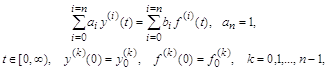
то его преобразование в систему уравнений первого порядка с новыми переменными 
осуществляется по следующим формулам:
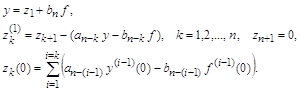
Такое преобразование сохраняет коэффициенты исходного уравнения неизменными и исключает производные в правой части от . Начальные условия для новых переменных здесь приходится пересчитывать по достаточно сложным соотношениям.
И, наконец, приведем еще один вариант разложения на систему уравнений первого порядка исходного неоднородного уравнения с производными в правой части:
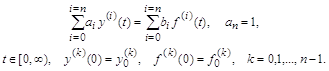
Замена переменных в отличие от предыдущего случая производится без сохранения коэффициентов исходного уравнения:
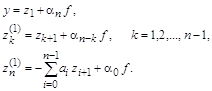
Производные искомой функции 
можно выразить через вновь введенные переменные 
путем многократного дифференцирования левой и правой части соотношения для y с подстановкой после каждого дифференцирования производных 
:
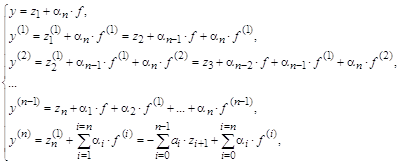
Умножив каждое выражение для 
на коэффициенты 
и просуммировав правые и левые члены равенств, получим уравнение, которое отличается от исходного лишь коэффициентами при производных в правых частях. Чтобы добиться тождественности, необходимо коэффициенты при соответствующих производных приравнять и разрешить полученную систему уравнений относительно неизвестных 
.
Система уравнений имеет вид:
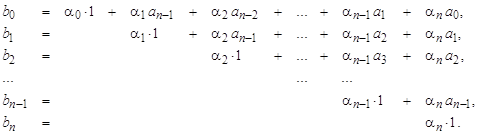
В векторно-матричной форме это уравнение и его решение записываются в следующем виде:
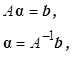
где 
– вектор известных коэффициентов,
– вектор искомых коэффициентов,
– соответственно прямая и обратная верхне-треугольные матрицы коэффициентов. Первая из них выглядит так:
.
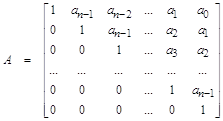Обратная матрица удобна при использовании математических пакетов для решения векторно-матричного уравнения. Если 
, то коэффициенты 
легко вычисляются последовательной подстановкой значений , начиная с 
.
Начальные условия для 
вычисляются по выражениям для 
следующим образом:
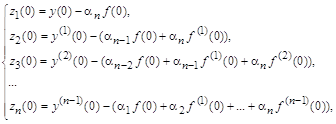
или в векторно-матричной форме:
,
.
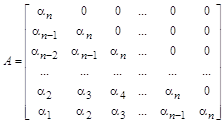Похожие работы
... схема со сглаживанием, схема прямоугольник со сглаживанием, “шахматная ” схема. Произведены некоторые расчеты для одномерного уравнения переноса с переменными и постоянными коэффициентами на неравномерных сетках, с целью определения наиболее устойчивой разностной схемы. Исследование показало, что наиболее устойчивым методом для одномерного уравнения переноса с переменными коэффициентами является ...
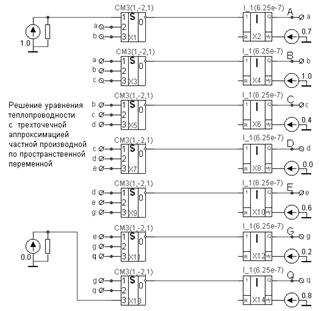
... . Результаты моделирования можно просматривать на экране монитора и распечатывать на принтере. В данном расчетно-графическом задании виртуальная гибридная вычислительная машина будет использована в качестве вычислительного инструмента для решения краевых задач методами математического и аналогового моделирования, с целью демонстрации возможностей аналоговых устройств для исследования физических ...
... ^у^е^о ^ с^-^. Итак решение по Ритцу: ^-i-^ Сравнительная таблица имеет вид: Л. 0 0,5 1 1,5 2 у^ 0 -0,275 -0,3571 -0,2758 0 ^г) о -0,2126 -0,3520 -0,3258 0 50 3.6. Об одном подходе к решению нелинейных вариационных задач В отличии от метода Ритца, искомую функцию в двуточечной вариационной задаче зададим в виде: r-^^f^-^^ При этом граничные условия и{а ) = ...
... суммы и позволит вычислить приближенное значение приращения Dy: где Метод четвертого порядка для q = 3, имеет вид где Особо широко известно другое вычислительное правило Рунге-Кутта четвертого порядка точности: где Метод Рунге-Кутта имеет погрешность четвертого порядка (~ h4 ). Правило Рунге. Если приближенный метод имеет порядок погрешности m, то погрешность можно приближенно ...
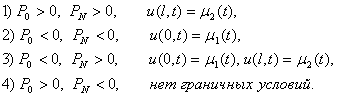
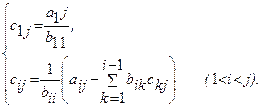
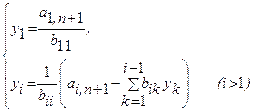
0 комментариев