Навигация
1. Первый метод
Группы | f | x |
|
|
|
|
| До 10 | 4 | 5 | -3 | 9 | -12 | 36 |
| 10-20 | 28 | 15 | -2 | 4 | -56 | 112 |
| 20-30 | 45 | 25 | -1 | 1 | -45 | 45 |
| 30-40 | 39 | 35 | 0 | 0 | 0 | 0 |
| 40-50 | 28 | 45 | 1 | 1 | 28 | 28 |
| 50-60 | 15 | 55 | 2 | 4 | 30 | 60 |
| 60 и выше | 10 | 65 | 3 | 9 | 30 | 90 |
| Итого | 169 | - | - | - | -25 | 371 |
Условное начало С = 35
Величина интервала d = 10
Первый условный момент:
Средний уровень признака:
Второй условный момент:
Дисперсия признака:
2. Второй метод
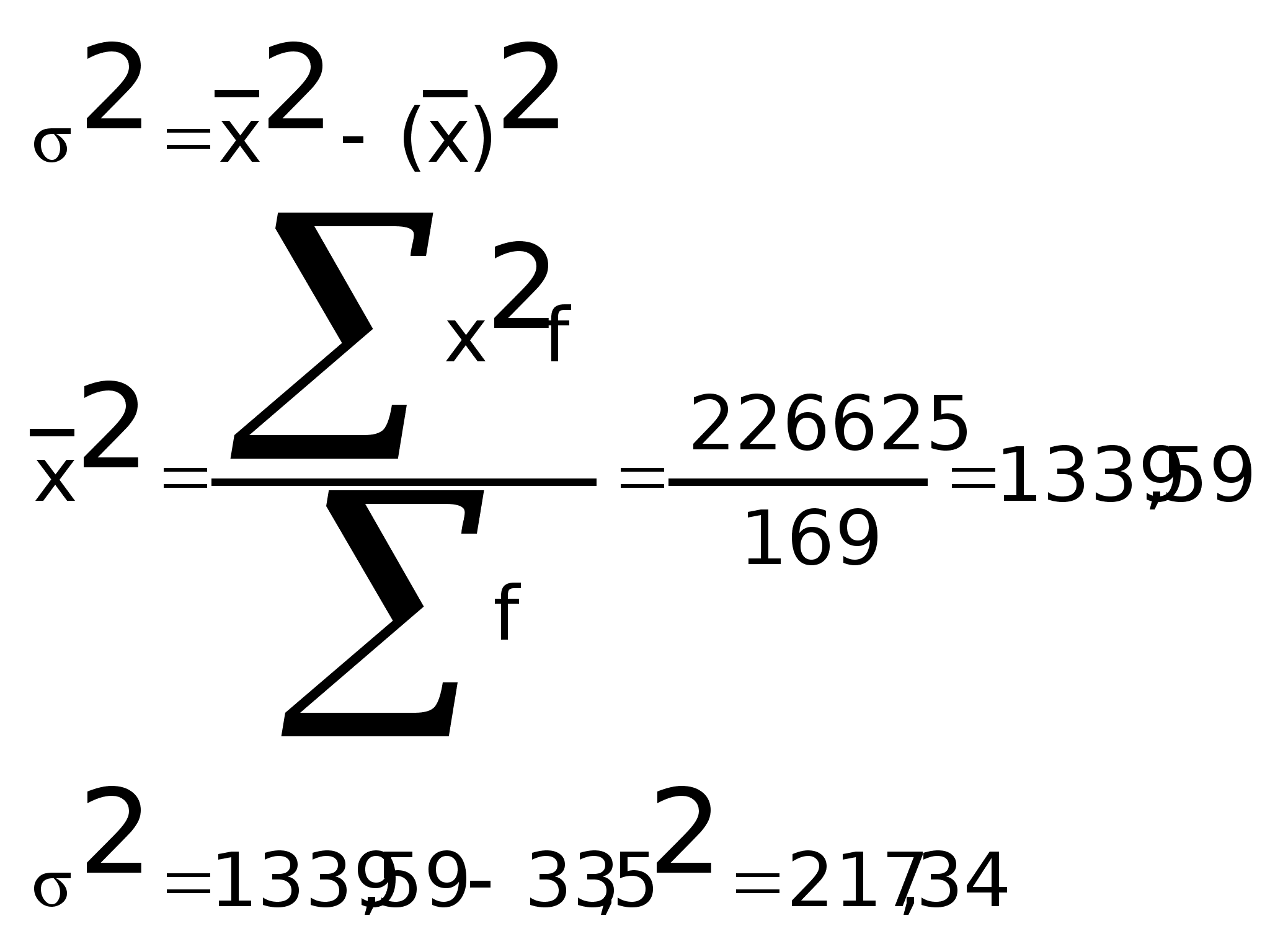
Методика расчета дисперсии альтернативного признака:
Альтернативным называется признак, который принимает значение «да» или «нет». Этот признак выражает как количественный «да»-1, «нет»-0, это значение x , тогда для него надо определить среднюю и дисперсию.
Вывод формулы:
| Признак х | 1 | 0 | всего |
| Ч | p | g | p + g = 1 |
| xf | 1p | 0g | p + 0 = p |
астота f вероятность
Средняя альтернативного признака равна доле единиц, которые этим признаком обладают.
|
|
|
| |
|
|
|
| |
|
|
|
|
|
- Дисперсия
альтернативного
признака. Она
равна произведению
доли единиц,
обладающих
признаком на
ее дополнение
до 1.
Дисперсия альтернативного признака используется при расчете ошибки для доли.
| p | g |
|
| 0,1 | 0,9 | 0,09 |
| 0,2 | 0,8 | 0,16 |
| 0,3 | 0,7 | 0,21 |
| 0,4 | 0,6 | 0,24 |
| 0,5 | 0,5 | max 0,25 |
| 0,6 | 0,4 | 0,24 |
,
W
– выборочная
доля.
Виды дисперсии и правило их сложения:
Виды:
1. Межгрупповая дисперсия.
2. Общая дисперсия.
3. Средняя дисперсия.
4. Внутригрупповая дисперсия.
У всей совокупности может быть рассчитана общая средняя и общая дисперсия.
1. 
общая и 
общая.
2. По
каждой группе
определяется
своя средняя
величина и своя
дисперсия:
a,a;
б,б;
i,i
3.
Групповые
средние i не одинаковые. Чем больше
различия между
группами, тем
больше различаются
групповые
средние и отличаются
от общей средней.
Это позволяет рассчитать дисперсию, которая показывает отклонение групповых средних от общей средней:
- межгрупповая
дисперсия, где
mi
– численность
единиц в каждой
группе.
В
каждой группе
имеется своя
колеблемость
– внутригрупповая
.
Она не одинакова,
поэтому определяется
средняя из
внутригрупповых
дисперсий: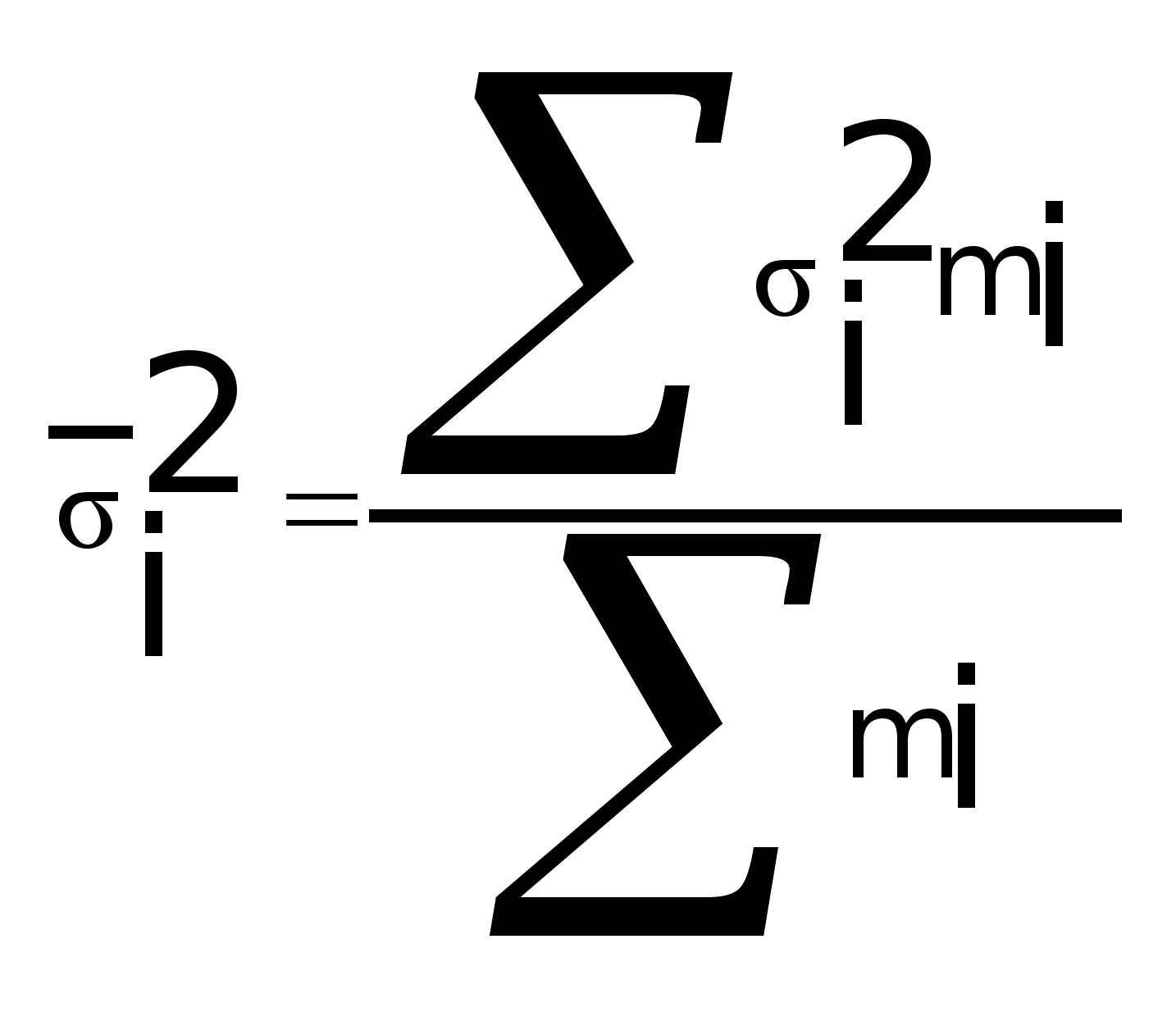 
Эти дисперсии находятся в определенном соотношении. Общая дисперсия равна сумме межгрупповой и средней из внутригрупповых дисперсий:
- правило
сложения дисперсий.
Соотношения дисперсий используются для оценки тесноты связей между факторами влияния изучаемого фактора – это межгрупповая дисперсия. Все остальные факторы – остаточные факторы.
Похожие работы
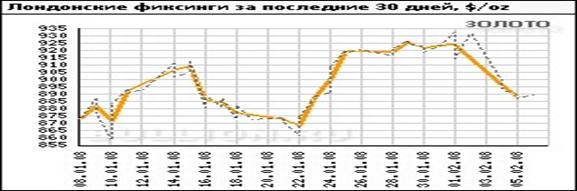
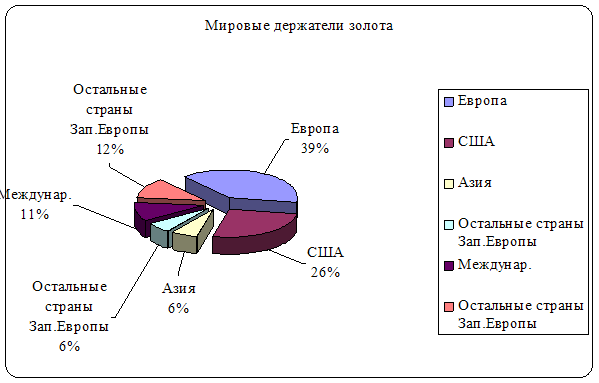
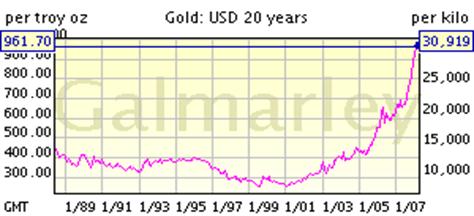
... динамики курса доллара и цен на золото. Разнонаправленность движения этих показателей обусловлена историческим ходом конкурентной борьбы, которую вели между собой доллар и золото за право верховенства в рамках мировой валютной системы. Следовательно, факторы, вызывающие снижение курса доллара (прежде всего, ухудшение общеэкономической ситуации в США), в той или иной мере могут стимулировать рост ...
... фондов и не подлежат изъятию на какие-либо цели, прямо не предусмотренные законом; 6) расходование средств из фондов осуществляется по распоряжению Правительства РФ или специально уполномоченного на то органа (правление фонда. Государственными внебюджетными фондами Российской Федерации являются: 1) Пенсионный фонд Российской Федерации; 2) Фонд социального страхования Российской Федерации; ...
... а самых активных. Их зовут лидерами общественного мнения. Нарушения социальных норм могут быть серьёзными и несерьёзными, сознательными и несознательными. Алкоголизм и наркомания – типичный вид девиантного поведения. Алкоголик и наркоман – не только больной человек, но и девиант, он не способен нормально выполнять социальные роли. Самоубийство, т.е. свободное и намеренное прекращение своей жизни, ...
0 комментариев