Навигация
1 EI=0.
S=S+1
do I=1,N
NEXTQ=y(3,i)*Q(y(1,i)-1,y(2,i))+
+ y(4,i)*Q(y(1,i),y(2,i)-1)+
+ y(5,i)*Q(y(1,i)+1,y(2,i))+
+ y(6,i)*Q(y(1,i),y(2,i)+1)
c------------------------------------------------------------------
c вычисление погрешности на данной итерации
c------------------------------------------------------------------
if (abs(NEXTQ-q(y(1,i),y(2,i))).gt.EI)
+ EI=abs(NEXTQ-q(y(1,i),y(2,i)))
c print *,'x=',y(1,i),' y=',y(2,i)
q(y(1,i),y(2,i))=NEXTQ
enddo
c print '(16h Итерация номер ,i5,13h погрешность=,E15.7)',S,EI
if (EI.gt.E)goto 1
c do i=P,1,-1
c print '(21e10.3)',(q(j,i),j=1,M)
c enddo
end
ТЕСТ
В качестве теста выполним одну итерацию для системы , полученной в предыдущем пункте.
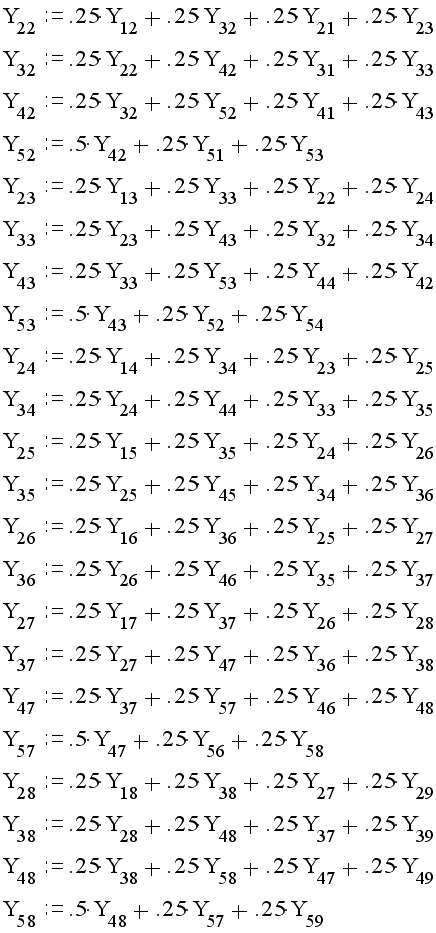
при начальных условиях:

все остальные Yij:=0.
Получается:
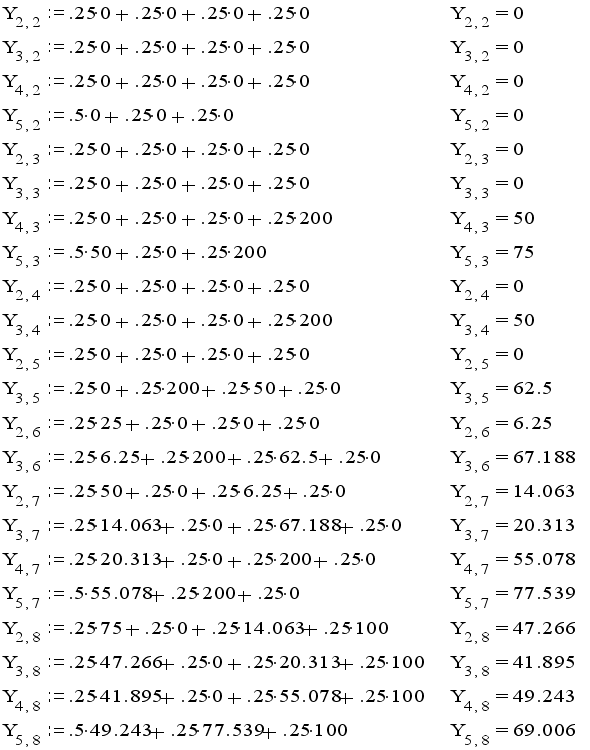
Результат:
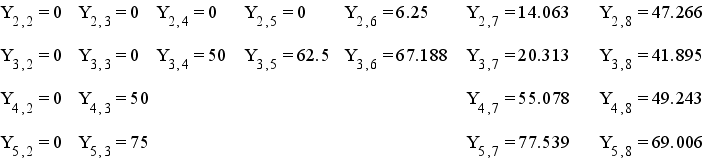
Полный текст программы.
c------------------------------------------------------------------
c ПОДПРОГРАММА СОСТАВЛЕНИЯ СИСТЕМЫ УРАВНЕНИЙ
c МЕТОДОМ КОНЕЧНЫХ РАЗНОСТЕЙ
c
c real H-шаг по оси X
c real K-шаг по оси Y
c real N-количество уравнений(примерное число,желательно N=M*P)
c real y(6,N)-выходной массив уравнений,содержащий следующие поля:
c y(1,N)-номер точки по оси X
c y(2,N)-номер точки по оси Y
c y(3,N)-коэфициен уравнения для Q(y(1,N)-1,y(2,N))
c y(3,N)=h^2/(2*(h^2+k^2))
c y(4,N)-коэфициен уравнения для Q(y(1,N),y(2,N)-1)
c y(4,N)=k^2/(2*(h^2+k^2))
c y(5,N)-коэфициен уравнения для Q(y(1,N)+1,y(2,N))
c y(5,N)=h^2/(2*(h^2+k^2))
c y(6,N)-коэфициен уравнения для Q(y(1,N),y(2,N)+1)
c y(6,N)=k^2/(2*(h^2+k^2))
c integer M-число узлов по оси X
c integer P-число узлов по оси Y
c real Q(M,P)-массив значений Y
c integer N-выходное количество получившихся уравнений
c------------------------------------------------------------------
subroutine mkr(H,K,N,y,M,P,q)
integer M,P,IIX,IIY,NN,N,KR1,KR2,KR3
real y(6,N),H,K,q(M,P),HX,KY
c-----------------------------------------------------------------
c подсчитываю коэфициенты
c h^2/(2*(h^2+k^2))
c и
c k^2/(2*(h^2+k^2))
c-----------------------------------------------------------------
HX=H**2/(2*(H**2+K**2))
KY=K**2/(2*(H**2+K**2))
c-----------------------------------------------------------------
c составление уравнений
c и
c присваивание начальных значений
c
c nn-счетчик уровнений
c iix-номер текущего узла по оси X
c iiy-номер текущего узла по оси Y
c-----------------------------------------------------------------
NN=0
KR1=((P-1)/8)*3+1
KR2=((P-1)/8)*5+1
KR3=((M-1)/4)*3+1
do IIY=2,P-1
do IIX=2,M
if (NN.eq.N)then
print *,'ПЕРЕПОЛНЕНИЕ МАССИВА Y'
stop
endif
c-----------------------------------------------------------------
c проверка границы трубы с жидкостью
c-----------------------------------------------------------------
if ((IIY.ge.KR1).and.(IIY.le.KR2).and.(IIX.ge.KR3)) then
q(IIX,IIY)=200.
c-----------------------------------------------------------------
c проверка симметрии
c-----------------------------------------------------------------
elseif (((IIY.lt.KR1).or.(IIY.gt.KR2)).and.(IIX.eq.M)) then
q(IIX,IIY)=6
NN=NN+1
y(1,NN)=IIX
y(2,NN)=IIY
y(3,NN)=2*HX
y(4,NN)=KY
y(5,NN)=0
y(6,NN)=KY
c-----------------------------------------------------------------
c составление уравнений во внутренних точках фигуры
c-----------------------------------------------------------------
else
q(IIX,IIY)=5
NN=NN+1
y(1,NN)=IIX
y(2,NN)=IIY
y(3,NN)=HX
y(4,NN)=KY
y(5,NN)=HX
y(6,NN)=KY
endif
enddo
enddo
c-----------------------------------------------------------------
c присваивание начальных значений на границе фигуры
c------------------------------------------------------------------
KY=0
KR1=P/2+1
do IIY=1,P
if (IIY.le.KR1)then
q(1,IIY)=0
else
q(1,IIY)=500*KY-100
endif
KY=KY+K
enddo
do IIX=1,M
q(IIX,1)=0
q(IIX,P)=100
enddo
N=NN
end
c-----------------------------------------------------------------
c ПОДПРОГРАММА РЕШЕНИЯ СИСТЕМЫ УРАВНЕНИЙ МЕТОДОМ ЗЕЙДЕЛЯ
c
с integer N-входное количество уравнений
c real y(6,N)-входной массив уравнений,содержащий следующие поля:
c y(1,N)-номер точки по оси X
c y(2,N)-номер точки по оси Y
c y(3,N)-коэфициен уравнения для Q(y(1,N)-1,y(2,N))
c y(3,N)=h^2/(2*(h^2+k^2))
c y(4,N)-коэфициен уравнения для Q(y(1,N),y(2,N)-1)
c y(4,N)=k^2/(2*(h^2+k^2))
c y(5,N)-коэфициен уравнения для Q(y(1,N)+1,y(2,N))
c y(5,N)=h^2/(2*(h^2+k^2))
c y(6,N)-коэфициен уравнения для Q(y(1,N),y(2,N)+1)
c y(6,N)=k^2/(2*(h^2+k^2))
c integer M-число узлов по оси X
c integer P-число узлов по оси Y
c real Q(M,P)-входной массив начальных значений Y
c real Q(M,P)-выходной массив вычисленых значений Y
c real E-погрешность вычислений
c------------------------------------------------------------------
subroutine zeidel(N,y,M,P,q,E)
integer N,M,P,I,S
real y(6,N),q(M,P),E,EI,NEXTQ
c------------------------------------------------------------------
c вычисление коэфициента сходимости процесса
c mj=y(5,1)+y(6,1)
c и выражения
c km=mj/(1-mj)
C НО Т.К. MJ=0.5 ТО KM=1 И СЛЕДОВАТЕЛЬНО ЕГО МОЖНО ОПУСТИТЬ
c-----------------------------------------------------------------
c KM=(y(5,1)+y(6,1))/(1-y(5,1)+y(6,1))
c------------------------------------------------------------------
c итерации
c S-счетчик итераций
c------------------------------------------------------------------
S=0
1 EI=0.
S=S+1
do I=1,N
NEXTQ=y(3,i)*Q(y(1,i)-1,y(2,i))+
+ y(4,i)*Q(y(1,i),y(2,i)-1)+
+ y(5,i)*Q(y(1,i)+1,y(2,i))+
+ y(6,i)*Q(y(1,i),y(2,i)+1)
c------------------------------------------------------------------
c вычисление погрешности на данной итерации
c------------------------------------------------------------------
if (abs(NEXTQ-q(y(1,i),y(2,i))).gt.EI)
+ EI=abs(NEXTQ-q(y(1,i),y(2,i)))
c print *,'x=',y(1,i),' y=',y(2,i)
q(y(1,i),y(2,i))=NEXTQ
enddo
c print '(16h Итерация номер ,i5,13h погрешность=,E15.7)',S,EI
if (EI.gt.E)goto 1
c do i=P,1,-1
c print '(21e10.3)',(q(j,i),j=1,M)
c enddo
end
c------------------------------------------------------------------
c ПОДПРОГРАММА АЛФАВИТНО-ЦИФРОВОГО,МОЗАИЧНОГО
c ВЫВОДА РЕЗУЛЬТАТА
c integer M-число узлов по оси X
c integer P-число узлов по оси Y
c real Q(M,P)-входной массив значений Y
c
c
c------------------------------------------------------------------
subroutine outdata(M,P,q)
character
a(11)/'.','+','*','','','-','-','-',''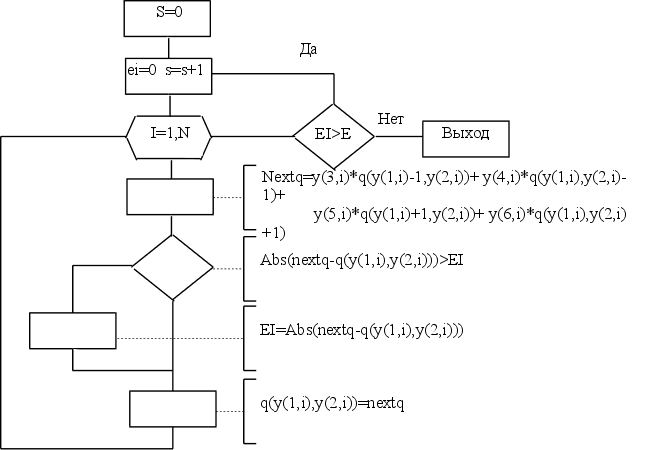 ,'-','-'/
,'-','-'/
integer M,P,I,J
real q(M,P)
do J=P,1,-1
print '(400A2)',(a(int(q(I,J)/21)+1),I=1,M),
+ (a(int(q(I,J)/21)+1),I=M-1,1,-1)
enddo
do I=1,10
print *,'''',a(I),'''','---> от ',20*(I-1),', до ',
+ 20*I,'(включительно)'
enddo
end
c------------------------------------------------------------------
c ПОДПРОГРАММА ВЫЧИСЛЕНИЯ ОШИБКИ
c real q-массив значений Y с шагом =2*h
c real qq-массив значений Y с шагом =h
c real E-значение погрешности
c
c------------------------------------------------------------------
subroutine mistake(M,P,q,qq,E)
integer M,P,iq,jq,iqq,jqq
real qq(M,P),q(int(M/2)+1,int(P/2)+1),max,E,other
max=0
iq=0
do iqq=1,P,2
iq=iq+1
jq=0
do jqq=1,M,2
jq=jq+1
other=abs(q(jq,iq)-qq(jqq,iqq))
if (other.gt.max)max=other
enddo
enddo
print *,M,' ',P,' ',max/3
if (max/3.lt.E) then
call outdata(M,P,qq)
Stop
endif
end
c------------------------------------------------------------------
c ОСНОВНАЯ ПРОГРАММА
c
c
c------------------------------------------------------------------
integer N/90000/,M,P,flag/0/
real y(6,90000),q(300,300),H/.05/,K/.05/,E/.5/,qq(300,300)
real EZ/.01/
c print *,'Введите шаг вдоль оси X '
c read (*,*)H
c print *,'Введите шаг вдоль оси Y '
c read (*,*)K
c print *,'Введите точность вычислений '
c read (*,*)E
M=.2/H+1
P=.4/K+1
call mkr(H,K,N,y,M,P,q)
call zeidel(N,y,M,P,q,EZ)
111 H=H/2
K=K/2
M=.2/H+1
P=.4/K+1
N=90000
if (flag.eq.0)then
flag=1
call mkr(H,K,N,y,M,P,qq)
call zeidel(N,y,M,P,qq,EZ)
call mistake(M,P,q,qq,E)
else
flag=0
call mkr(H,K,N,y,M,P,q)
call zeidel(N,y,M,P,q,EZ)
call mistake(M,P,qq,q,E)
endif
goto 111
end
Литература.
1. И.С.Березин,Н.П.Жидков ’Методы вычислений’,том 1,М.,1966,632 стр.
2.’ Численные методы решения задач на ЭВМ ’ , Учебное пособие , Г.Н.Рубальченко , К. , 1989 , 148 стр.
3.’Справочник языка ФОРТРАН’ , М.,1996 ,106 стр.
Температурный расчет с помощью вычислений информационной матема
Похожие работы
... быть выведены на печать. На экране рисунки могут быть статическими (неподвижными) или динамическими (движущимися). В последнее время машинная графика выделилась в самостоятельный раздел информатики с многочисленными приложениями. Средствами машинной графики создается не только печатная продукция, но и рекламные ролики на телевидении, мультфильмы. Объясним, как кодируется изображение в памяти ...
... хранение больших массивов измерительной информации. Следствием этого является схожесть структур, обязательное использование ЭВМ и соответствующего ПМО. Заключение В работе рассмотрены примеры измерительных информационных систем для исследования объектов различной физической природы. Литература 1. Автоматизация физических исследований и эксперимента: компьютерные измерения и виртуальные ...
... ранее компьютерных технологий, применяемых на этапах разработки объекта машиностроительного профиля, приведена в Приложении А. Глава 2. Современные компьютерные технологии при проектировании высокомоментного линейного привода с цифровым программным управлением Привод линейный синхронный представляет собой комплектный привод прямого действия на базе однокоординатного синхронного линейного ...
... выданных книг, фиксацию возврата книг, просмотра и распечатки отчета задолжников, списание формуляров в архив. 3.5 Расчет вычислительных ресурсов, необходимых для функционирования автоматизированной информационной библиотечной системы АРМ администратора, каталогизатора и библиотекаря объединены (разделение нецелесообразно, так как новые поступления литературы и периодики невелики). Для ...

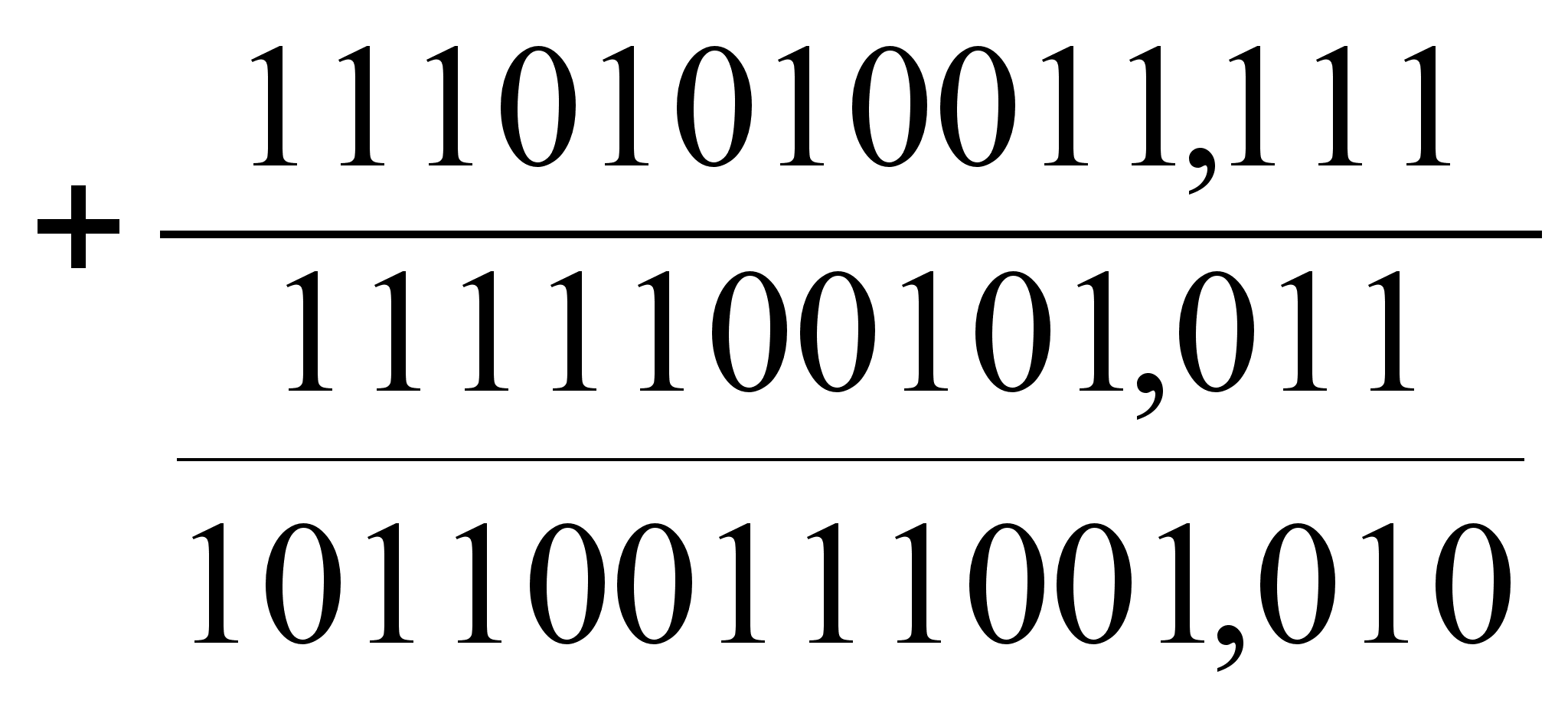


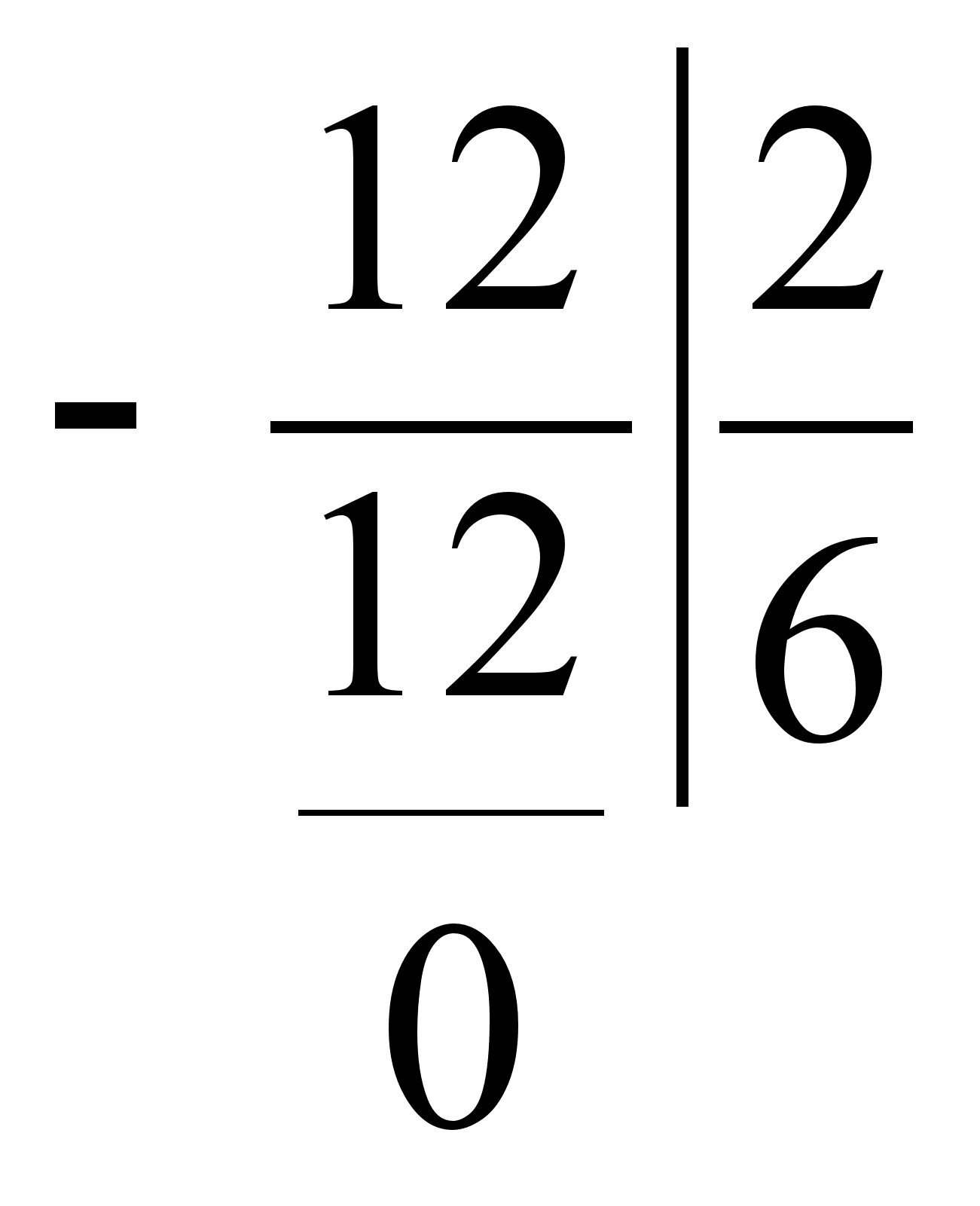
0 комментариев