Навигация
Закон равномерной плотности вероятности
3. Закон равномерной плотности вероятности.
В некоторых задачах практики встречаются непрерывные случайные величины, о которых заранее известно, что их возможные значения лежат в пределах некоторого определенного интервала; кроме того, известно, что в пределах этого интервала все значения случайной величины одинаково вероятны (точнее, обладают одной и той же плотностью вероятности). О таких случайных величинах говорят, что они распределяются по закону равномерной плотности.
Дадим определение: равномерным называется распределение непрерывной случайной величины Х все значения которой лежат на отрезке [a;b] и имеют при этом постоянную плотность распределения:

площадь под кривой распределения равна 1 и поэтому с(в-а)=1

вероятность попадания случайной величины Х на интервал от (α;β)
![]()
α=а, если α<а
β=в, если β>в
основные числовые характеристики закона распределения плотности вычисляются по общим формулам и они равны

Приведем примеры подобных случайных величин:
Пример 1. Произведено взвешивание тела на точных весах, но в распоряжении взвешивающего имеются только разновески весом не менее 1г.; результат взвешивания показывает, что вес тела заключен между k и (k+1/2) граммам. Допущенная при этом ошибка X , очевидно, есть случайная величина, распределенная с равномерной плотностью на участке  г.
г.
Пример 2. Вертикально поставленное симметричное колесо (см.Рисунок№1) приводится во вращение и затем останавливается вследствие трения. Рассматривается случайная величина θ –угол, который после остановки будет составлять с горизонтом фиксированный радиус колеса ОА. Очевидно величина θ распределена с равномерной плотностью на участке (0,2 π)
| Рисунок 1 |

Итак, я рассмотрю случайные величины и функции распределения.
4. Случайные величины
Определение. Пусть ![]() — произвольное вероятностное пространство.
— произвольное вероятностное пространство.
Случайной величиной ![]() называется измеримая функция
называется измеримая функция ![]() , отображающая
, отображающая ![]() в множество действительных чисел
в множество действительных чисел ![]() , т.е. функция, для которой прообраз
, т.е. функция, для которой прообраз ![]() любого борелевского множества
любого борелевского множества ![]() есть множество из
есть множество из ![]() -алгебры
-алгебры ![]() .
.
Примеры случайных величин. 1) Число выпавшее на грани игральной кости.
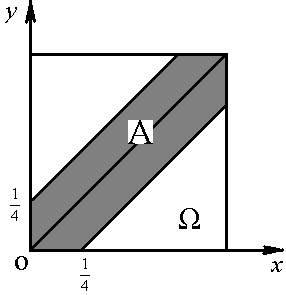
2) Размер выпускаемой детали. 3) Расстояние от начала координат до случайно брошенной в квадрат точки ![]() .
.
Множество значений случайной величины ![]() будем обозначать
будем обозначать ![]() , а образ элементарного события
, а образ элементарного события ![]() —
— ![]() . Множество значений
. Множество значений ![]() может быть конечным, счетным или несчетным.
может быть конечным, счетным или несчетным.
Определим ![]() -алгебру на множестве
-алгебру на множестве ![]() . В общем случае
. В общем случае ![]() -алгебра числового множества
-алгебра числового множества ![]() может быть образована применением конечного числа операций объединения и пересечения интервалов
может быть образована применением конечного числа операций объединения и пересечения интервалов ![]() или полуинтервалов вида
или полуинтервалов вида ![]() (
(![]() ), в которых одно из чисел
), в которых одно из чисел ![]() или
или ![]() может быть равно
может быть равно ![]() или
или ![]() .
.
В частном случае, когда ![]() — дискретное (не более чем счетное) множество,
— дискретное (не более чем счетное) множество, ![]() -алгебру образуют любые подмножества множества
-алгебру образуют любые подмножества множества ![]() , в том числе и одноточечные.
, в том числе и одноточечные.
Таким образом ![]() -алгебру множества
-алгебру множества ![]() можно построить из множеств
можно построить из множеств ![]() или
или ![]() , или
, или ![]() .
.
Будем называть событием ![]() любое подмножество значений
любое подмножество значений ![]() случайной величины
случайной величины ![]() :
: ![]() . Прообраз этого события обозначим
. Прообраз этого события обозначим ![]() . Ясно, что
. Ясно, что ![]() ;
; ![]() ;
; ![]() . Все множества
. Все множества ![]() , которые могут быть получены как подмножества
, которые могут быть получены как подмножества ![]() из множества
из множества ![]() ,
, ![]() , применением конечного числа операций объединения и пересечения, образуют систему событий. Определив множество возможных значений случайной величины
, применением конечного числа операций объединения и пересечения, образуют систему событий. Определив множество возможных значений случайной величины ![]() —
— ![]() и выделив систему событий
и выделив систему событий ![]() , построим измеримое пространство
, построим измеримое пространство ![]() . Определим вероятность на подмножествах (событиях)
. Определим вероятность на подмножествах (событиях) ![]() из
из ![]() таким образом, чтобы она была равна вероятности наступления события, являющегося его прообразом:
таким образом, чтобы она была равна вероятности наступления события, являющегося его прообразом: ![]() .
.
Тогда тройка ![]() назовем вероятностным пространством случайной величины
назовем вероятностным пространством случайной величины ![]() , где
, где ![]()
— множество значений случайной величины ![]() ;
; ![]() —
— ![]() -алгебра числового множества
-алгебра числового множества ![]() ;
; ![]() — функция вероятности случайной величины
— функция вероятности случайной величины ![]() .
.
Если каждому событию ![]() поставлено в соответствие
поставлено в соответствие ![]() , то говорят, что задано распределение случайной величины
, то говорят, что задано распределение случайной величины ![]() . Функция
. Функция ![]() задается на таких событиях (базовых), зная вероятности которых можно вычислить вероятность произвольного события
задается на таких событиях (базовых), зная вероятности которых можно вычислить вероятность произвольного события ![]() . Тогда событиями могут быть события
. Тогда событиями могут быть события ![]() .
.
Похожие работы
... тем отчетливее, чем длиннее серия. Все это вместе взятое заставляет искать способы однозначного определения меры возможности наступления случайного события, причем до испытания, до опыта. Вначале определим вероятность регулярного случайного события как число, около которого колеблется относительная частота в длинных сериях испытаний. Затем введем понятие равновозможности, равновероятности двух ...
... , что вероятнее выиграть у равносильного противника три партии из пяти чем пять из восьми. Задача 13А. Из партии, в которой 25 изделий, среди которых 6 бракованных, случайным образом выбрали 3 изделия для проверки качества. Найти вероятность того, что: а) все изделия годные, б) среди выбранных изделий одно бракованное; в) все изделия бракованные. Решение: а) Пусть событие А состоит в том, ...
... нашем примере: сила, с которой брошена монета, форма монеты и многие другие). Невозможно учесть влияние на результат всех этих причин, поскольку число их очень велико и законы их действия неизвестны. Поэтому теория вероятностей не ставит перед собой задачу предсказать, произойдет единичное событие или нет, она просто не в силах это сделать. Еще пример, выпадение снега в Москве 30 ноября является ...
... ничего другого, кроме как опять же события и . Действительно, имеем: *=, *=, =, =. Другим примером алгебры событий L является совокупность из четырех событий: . В самом деле: *=,*=,=,. 2.Вероятность. Теория вероятностей изучает случайные события. Это значит, что до определенного момента времени, вообще говоря, нельзя сказать заранее о случайном событии А произойдет это событие или нет. Только ...
0 комментариев