N-1

_{3 n-1} (5.16)

 …………..

 a_{n-1 n-1}

Отсюда для получения следующегоопределителя можно применить правило, условно назовем, треугольника.

a₁₁= a₁₁ a₂₂- a₁₂²

a₂₂= a₁₁ a₃₃- a₁₃² и т.д.

Для недиагоналных элементов схема несколько сложнее

a₁₂= a₁₁ a₂₃- a₁₃ a₁₂  a₁₁ a₁₂ а₁₃

а₂₃ и т.д.

Пример №3.

Исследовать на экстремум функцию z=x³+y³-3xy

1.Находим

z z

---- и ----

y x

z

---- = 3x²-3y

y

z

---- = 3y²-3x

x

2.Находим стационарные точки, решая систему

3x²-3y=0

3y²-3x=0

Получили две стационарные точкм (0;0) и (1;1).

3.Находим

²z ²z ²z

------- --------- --------

x² y² x y

 

²z ²z ²z

------- =6x --------- =6y -------- = -3

x² y²  x y

 

4.Для точки (0;0) имеем

a₁₁=0 a₂₂=0 a₁₂= a₂₁= -3

Для точки (1;1) иммем

b₁₁=6 b₂₂=6 a₁₂= a₂₁= -3

5.Находим

a₁₁ a₁₂  0 -3

a₂₁ a₂₂ -3 0

b₁₁ b₁₂ 6 -3

b₂₁ b₂₂ -3 6

Так как <0 , то в точке (0;0) экстремума нет.

Так как >0 и a₁₁>0, то (1;1) – точка минимма функции, причем z_min = -1.

Пример №4.

Исследовать на экстремум функцию w=x^2/3+y^2/3+z^2/3

Ищем критические точки

 2 2 2

w`<sub>x</sub>= ------ w`_y= --------- w`_z= ----------

3 ³ x 3 ³ y 3 ³ z

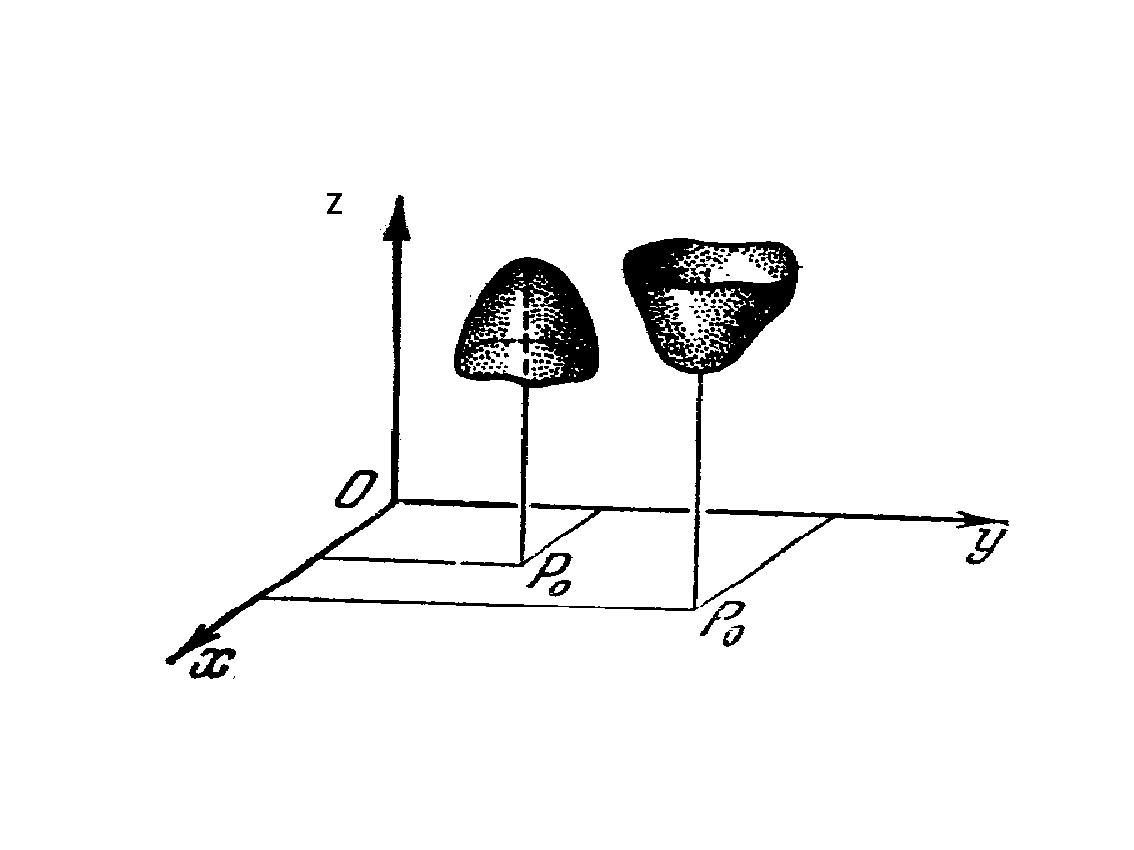
Эти частные производные не обращаются в нуль ни при каких значениях x, y, z; они не сужествуют (обращаются в бесконечность) в точке P₀(0;0;0). Точка P₀ лежит внутри области определения функции w, которая представляет совокупность всех точек (x;y;z) пространства. Поэтому P₀ критическая точка.

Исследуя знак разности w(P)-w(P₀)= x^2/3+y^2/3+z^2/3 вблизи точки P₀, убеждаемся, что при любых отличных от нуля значениях x,y,z она сохраняет положительный знак. Поэтому P₀ есть точка минимума, w_min=w(P₀)=0

5.4.Экстремумы на множествах.

Следует обратить внимание на то, что мы указали необходимые и достаточные условия экстремума функции лишь во внутренней точке области определения. Таким образом, при отыскании абсолютного максимума или минимума функции необходимо наряду с внутренними критическими точками функции исследовать также точки границы области определения, поскрльку максимальное или минимальное значение функция может принять в одной из таких граничных точек.

Пусть функция f дифференцируема на открытом ограниченом G и непрерывна на его замыкании G. Пусть требуется найти наибольшее и наименьшее значения функции на множестве G. Для этого можно, например, найти все стационарные точки функции f в G, вычислить в них значения функции и выбрать, если, конечно это возможно (а теоретически возможно это, например, когда число стационарных точек конечно), точки, в которых функция принимает наибольшее и наименьшее значения из всех значений в стационарных точках. После этого следует сравнивать эти значения со значениями, которые функция принимает на границе открытого множества G, например, найдя, если это удается сделать, наибольшее и наименьшее значения функции f на границе области G. Сравнив наибольшее и наименьшее значения в стационарных точках с наибольшим и наименьшим значениями на границе множества G, мы можем, очевидно, найти искомый максимум и минимум f на G.

В случае, когда G – плоская область и ее граница является кривой, заданной некоторым представлением x=x(t), y=y(t), <t< вопрос о нахождении экстремальных значений функции f(x,y) на границе G сводится к исследованию на экстремум функции одного переменного f(x(t),y(t)), что делается уже известными нами методами.

Методы, которые можно применять в многомерном случае для отыскания экстремальных точек на границе области будут рассмотрены позже (см. раздел, посвященный условному экстремуму).

Полезно лишь иметь ввиду, что при отыскании максимумов и минимумов часто наряду с формальной техникой, а иногда и вместо нее можно использовать некоторые простые соображения, связанные с природой задачи. Например, если рассматриваемая в Rⁿ дифференцируемая функция по смыслу задачи должна иметь минимум и вместе с тем она не ограничена сверху, то при условии, что функция имеет единственную критическую точку, можно без дальнейшего исследования утверждать, что в этой точке она принимает минимальное знычение.

6.Условный экстремум.

6.1.Постановка вопроса.

Одним из наиболее ярких популярных достижений дифференциального исчисления являются предполагаемые им рецепты отыскания экстремумов функций. Необходимые условия и достаточные дифференциальные признаки экстремума, которые мы получили из формулы Тейлора, относятся, как уже отмечалось к внутренним экстремумам.

Иными словами, эти результаты применимы только к исследованию поведения функции Rⁿ x f(x) R в окрестности точки тогда, когда аргумент может принимать любое значение из некоторой окрестности Rⁿ в точки x₀.

Часто возникает более сложная и с практической точки зрения даже более интересная ситуация,когда ищется экстремум функции при некоторых условиях, ограничивающих область измерения аргумента. Типичным примером может служить изопериметрическая задача, когда ищется тело, имеющее максимальный объем при условии, что ограничивающая его поверхность имеет заданную площадь. Чтобы получить доступную нам математичкую запись такой задачи, упростим постановку и будем считать, что задача состоит в том, чтобы среди прямоугольников, имеющих заданный периметр 2р, найти тот, который имеет наибольшую площадь . Обозначив через х и у длины сторон прымоугольника, запишем, что

(х,у)=х-у

х+у=р

Итак, надо найти экстремум функции (х,у) при условии, что переменные х,у связаны соотношением х+у=р. Таким образом, экстремум функции ищется только на множестве тех точек плоскости R², которые удовлетворяют указанному соотношению. Эта конкретная задача, конечно, решается без труда : достаточно, записав, что у=р-х, подставить это выражение в формулу для (х,у) и найти обычными методами максимум функции х(р-х). Она нам была нужна лишь для постановки вопрса. В следующих пунктах мы рассмотрим общий случай решения подобных задач.

6.2.Понятие условного экстремума.

Пусть на открытом множестве G Rⁿ заданы функции.

y_i=f_i(x) i=1,2,3,…,m (6.1)

x=(x₁,x₂,…,x_n).Обозначим через Е множество точек x G , в которых все функции f_i  i=1,2,3,…,m обращаются в нуль:

E={x: f_i(x)=0, i=1,2,3,…,m, x G} (6.2)

Уравнения

f_i(x)=0, i=1,2,3,…,n (6.3)

 будем называть уравнениями связи.

Определение : пусть на множестве G задана функция y=f₀(x) .Тогда x⁽⁰⁾  E называется точкой условного экстремума (принят также термин «относительный экстремум») функции f₀(x) относительно (или при выполнении) уравнений связи (6.3) , если она является точкой обычного экстремума этой функции , рассмотриваемой только на множестве Е.

Иначе говоря , здесь значения функции f₀(x) в точке x⁽⁰⁾ сравниваются не со всеми ее значениями в достаточно малой окрестности этой точки , а только со значениями в точках , принадлежащих одновременно указанной достаточно малой окрестности и множеству Е. Как и в случае обычных экстремумов , можно , естественно , рассматривать точки просто условного экстремума и точки строго условного экстремума.

Будем предполагать , что

1)   все функции f₀,f₁,f₂,…, f_m непрерывно дифференцируемы в открытом множестве G ;

2)   в рассматриваемой точке x⁽⁰⁾ векторы f₁, f₂,…, f_m линейно независимы , т.е. ранг матрицы Якоби

f_j  j=1,2,…,m

x_i i=1,2,…,n

равен m-числу ее строк (строки матрицы Якоби являются компонентами градиентов f₁, f₂,…, f_m).

Это означает , что функции системы (6.1) независимы в некоторой окрестности точки x⁽⁰⁾.Поскольку в n-мерном пространстве не может быть больше чем n линйено независимых векторов и ранг матрицы не может быть больше чиола столбцов , то из условия 2) следует ,что m<n.

Согласно условию 2) в точке x⁽⁰⁾ хотя бы один из определителей вида

 (f₁, f₂,…, f_m)

(x_i1,x_i2,…,x_im)

отличен от нуля.Пусть для определенности в точке x⁽⁰⁾.

(f₁, f₂,…, f_m)

(x_i1,x_i2,…,x_im) (6.4)

Тогда , в силу теоремы о неявных функциях , систему уравнений (6.3) в некоторой окрестности точки x⁽⁰⁾=(x₁⁽⁰⁾,x₂⁽⁰⁾,…,x_n⁽⁰⁾) можно разрешить относительно переменных x₁,x₂,…,x_m :

x₁= ₁( x₁,x₂,…,x_m)

x₂= ₂( x₁,x₂,…,x_m)

…………………… (6.5)

x_m= _m( x₁,x₂,…,x_m)

Поставив значения x₁,x₂,…,x_m, даваемые формулами (6.5) в y=f₀(x), т.е. рассмотрев композицию функции f₀ и ₁, получили функцию

y= f₀( ₁( x_m+1,…,x_n),…,  _m( x_m+1,…,x_n), x_m+1,…,x_n)== =0( x_m+1,…,x_n) (6.6)

от n-m переменных x_m+1,…,x_n,определенную и непрерывно дифференцируемую в некоторой окрестности точки x⁽⁰⁾=(x₁⁽⁰⁾,x₂⁽⁰⁾,…,x_n⁽⁰⁾) в (n-m)–мерном пространстве R^n-m.

Поскольку , согласно теореме о неявных функциях , условия (6.3) и (6.5) равносильны ,то справедливо следующее утверждение.

Точка x⁽⁰⁾ является точкой (строгого) условного экстремума для функции g относительно уравнений связи (6.3) в том и только том случае , когда x⁽⁰⁾ является точкой обычного (строгого) экстремума (6.6).

Если x⁽⁰⁾– точка обычного экстремума функции g, то она является стационарной точкой этой функции:

dg (x⁽⁰⁾)=0 (6.7)

Напомним , что дифференциал – линейная однородная функция и его равенство нулю означает равенство нулю этой функции при любых значениях ее аргументов , в данном случае – при любых dx_m+1, dx_m+2,…, dx_n.Это возможно ,очевидно , в том и только том случае , когда все коэффициенты при этих аргументах , т.е. производные g/ x_m+k, k=1,2,…,n-m обращаются в нуль в точке x⁽⁰⁾.Условие (6.7) необходимо для условного экстремума в точке x⁽⁰⁾.

Таким образом , метод , основанный на решение системы уравнений (6.3) через элементарные функции часто невозможно или весьма затруднительно; поэтому желательно располагать методом , позволяющим найти условный экстремум не решая системы (6.3).Такой способ ,так называемый метод множетелей Лагранжа , изложен в следующем пункте .

6.3.Метод множетелей Лагранжа для нахождения точек условного экстремума.

В этом пункте будем предполагать , что все функции f₀,f₁,f₂,…, f_m непрерывно дифференцируемы в открытом множестве G.

Теорема 6.1 : пусть x⁽⁰⁾– точка условного экстремума функции f₀ при выполнении уравнений связи (6.3).Тогда в этой точке градиенты f₁, f₂,…, f_m линейно независимы , т.е. существуют такие не все равные нулю , числа ₀,  ₁, ₂,…, _m что

₀  f₀+ ₁f₁+ ₂f₂+…+ _mf_m=0 (6.8)

Следствие : если в точке x⁽⁰⁾ условного экстремума функции f₀ относительно уравнений связи (6.3) градиенты f₁, f₂,…, f_m линейно независимы , то ранг матрицы Якоби

 f_j  j=1,2,…,m

x_i i=1,2,…,n

равен m, то существуют такие ₁,…,  _m , что в этой точке

 f₀+ _i f_j=0 (6.9)

т.е. f₀ является линейной комбинацией градиентов f₁, f₂,…, f_m.

В координатной форме это условие имеет вид : для любого i=1,2,…,n в точке x⁽⁰⁾

f₀ f_i

x_i x_i (6.10)

функция

F(x)==f₀(x)+ _jf_j(x) (6.11)

 где числа ₁,…,  _m удовлетворяют условию(6.10), называется функцией Лагранжа рассматриваемой задачи , а сами числа ₁,…,  _m – множителями Лагранжа.

Условие (6.10) означает , что если x⁽⁰⁾ является точкой условного экстремума функции f₀ относительно уравнений связи (6.3) , то она является стационарной точкой для функции Лагранжа , т.е.

F(x⁽⁰⁾)

x_i i=1,2,…,n (6.12)

Прежде , чем доказать теорему , разъясним ее смысл и покажем , как ее использовать для нахождения точек условного экстремума. Прежде всего обратим внимание на то , что у функции вида (6.11) при произвольных числах ₁,…,  _m, каждая точка ее условного экстремума является и точкой условного экстремума исходной функции f₀, и наоборот.Мы выбираем такие значения ₁,…,  _m, чтобы выполнялись условия (6.10) , т.е. чтобы данная точка условного экстремума оказалась и стационарной точкой фуцнкции (6.9).

Для отыскания точек условного экстремума следует рассмотреть систему n+m уравнений (6.3) и (6.8) относительно неизвестных x₁⁽⁰⁾,x₂⁽⁰⁾,…,x_n⁽⁰⁾,  ₁,…,  _m и решить ее (если это возможно) , найдя x₁⁽⁰⁾,x₂⁽⁰⁾,…,x_n⁽⁰⁾ и по возможности исключив ₁,…,  _m.Сформулированная теорема утверждает , что все точки условного экстремума будут находится среди найденных таким образом точек (x₁⁽⁰⁾,x₂⁽⁰⁾,…,x_n⁽⁰⁾).Вопрос о том , какие же из них фактически будут точками условного экстремума , требует дополнительного исследования , об этом будет говориться в п.6.5

Доказательство теоремы . Докажем утверждение равносильное теореме : если в точке x⁽⁰⁾=(x₁⁽⁰⁾,x₂⁽⁰⁾,…,x_n⁽⁰⁾), удовлетворяющей уравнениям связи

f_k(x⁽⁰⁾)=0 k=1,2,…,n (6.13)

градиенты f₀, f₁, f₂,…, f_m линейно независимы , то x⁽⁰⁾ не является точкой условного экстремума.

Итак , пусть f₀, f₁, f₂,…, f_m линейно независимы и , следовательно , ранг матрицы Якоби f_j/ x_i j=1,2,…,m,i=1,2,…,n равен m+1.Тогда в матрице существует минор порядка m+1 не равный нулю.Для определенности будем считать , что он образован первыми m+1 столбцами , т.е.

 (f₀, f₁, f₂,…, f_m)

(x₁,x₂,…,x_m+1) x=x⁽⁰⁾ (6.14)

Множество G–открыто , а поэтому существует такое 0₀>0, что при всех 0 0<0<0₀ , куб

Q  ⁿ={x: x_i-x_i⁽⁰⁾ <0,i=1,2,…,n}

лежит в G и , следовательно, на нем определены все функции f₀, f₁, f₂,…, f_m.

Зафиксируем x_m+2= x⁽⁰⁾_m+2,…, x_n=x_n⁽⁰⁾ и введем обозначения

x^*=(x₁,x₂,…,x_m+1)

Q ^m+1={x^*: x_i-x_i⁽⁰⁾ <0,i=1,2,…,m+1}

Очевидно , функции f_j(x₁,x₂,…,x_m+1,x⁽⁰⁾_m+2,…,x_n⁽⁰⁾) j=1,2,…,m определены и непрерывно дифференцируемы всюду в Q ^m+1.Рассмотрим отображение Ф : Q^m+1 R^m+1, задаваемое формулами

y₁= f₀(x₁,x₂,…,x_m+1,x⁽⁰⁾_m+2,…,x_n⁽⁰⁾)

y₂= f₁(x₁,x₂,…,x_m+1,x⁽⁰⁾_m+2,…,x_n⁽⁰⁾)

…………………………………… (6.15)

y_m+1= f_m(x₁,x₂,…,x_m+1,x⁽⁰⁾_m+2,…,x_n⁽⁰⁾)

В силу (6.15) для точки x^*(0)=(x₁⁽⁰⁾,x₂⁽⁰⁾,…,x_n⁽⁰⁾) имеем

(y₁, y₂,…, y_m+1) (f₀, f₁, f₂,…, f_m)

(x₁,x₂,…,x_m+1) x^*= x^*(0) (x₁,x₂,…,x_m+1) x=x⁽⁰⁾  

а в силу (6.13) Ф(x^*(0))=(f₀(x⁽⁰⁾,0,…,0) .Поэтому (в силу теремы о локальной обратимости непрерывно дифференцируемого отображения в точке , в которой его якобиан не равен нулю , существует такое число >0 , что на окрестности

V={y=(y₁, y₂,…, y_m+1) : y₁- f₀(x⁽⁰⁾) < , y_j< ,j=2,3,…,m}

(рис.5) определено обратное к Ф отображение и , следовательно , в любую точку этой окрестности отображается какая-то точка из Q ^m+1.

В частности , поскольку при любом n,0<n< ,имеет место включение (f₀(x⁽⁰⁾)+n,0,…,0), то в кубе найдутся точки x`<sup>*</sup>=(x`₁,x`<sub>2</sub>,…,x`_m+1)  и x``<sup>*</sup>=(x``₁,x``<sub>2</sub>,…,x``_m+1), отображающиеся при отображении Ф в указанные точки окрестностиV`.

Ф(x`^*)=(f₀(x⁽⁰⁾)+n,0,…,0)

Ф(x``^*)=(f₀(x⁽⁰⁾)-n,0,…,0)

Если положим для краткости x`=(x`₁,x`<sub>2</sub>,…,x`_m+1,x⁽⁰⁾_m+2,…,x_n⁽⁰⁾) и x``=(x``₁,x``<sub>2</sub>,…,x``_m+1,x⁽⁰⁾_m+2,…,x_n⁽⁰⁾), то в координатной записи (6.15) получим

f₀(x`)= f<sub>0</sub>(x<sup>(0)</sup>)+n> f(x<sup>(0)</sup>) , f<sub>k</sub>(x`)=0, k=1,2,…,n , x` Q ⁿ

 и

f₀(x``)= f<sub>0</sub>(x<sup>(0)</sup>)-n> f(x<sup>(0)</sup>) , f<sub>k</sub>(x``)=0, k=1,2,…,n , x`` Q ⁿ

В силу произвольности 0>0,0<0<0 , это и означает , что x⁽⁰⁾ не является точкой условного экстремума.

ч.т.д.

Доказательство следствея. Если векторы f₁, f₂,…, f_m линейно независимы , то в равенстве (6.8) имеем ₀=0 так как в случае ₀=0 указанные векторы в силу (6.8) оказались бы линейно зависимыми .Разделив обе части на ₀ получим равенство вида (6.9).

ч.т.д.

Пример №5.

 Пусть требуется найти экстремум функции u=xyzt при условии x+y+z+t=4c; область изменения переменных определяетссся неравенствовами x>0, y>0, t>0, z>0.

Применяя к этой задаче метод Лагранжа, введем вспомогательную функцию

Ф=xyzt+ (x+y+z+t)

И составим условия

Ф_x =yzt+ =0

Ф_y =xzt+ =0

Ф_z =yxt+ =0

Ф_t =yzx+ =0

откуда

yzt=xzt=xyt=xyz

так что

x=y=z=t=c.

6.4.Стационарные точки функции Лагранжа.

В этом пункте будет дано описаие стационарных точек функции Лагранжа (6.10) посредством фукции 0(x_m+1,x_m+2,…,x_n), введенной в пункте 6.2 (см.(6.8)).Предварительно докажем одну простую лемму из линейной алгебры.

Пусть задана система линейных однородных уравнений

a_i1x₁+…+ a_inx_n=0 i=1,2,…,m (6.16)

и еще одно линейное однродное уравнение

b₁x₁+…+ b_nx_n=0 (6.17)

Cистему уравнений , полученную присоединением к системе (6.16) уравнения (6.17), будем называть расширенной системой (6.16)-(6.17).

Лемма: Для того чтобы расширенная система (6.16)-(6.17) была равносильна основной системе (6.16) необходимо и достаточно , чтобы уравнение (6.17) являлось линейной комбинацией уравнений системы (6.16).

Следствие:Для того чтобы уравнение (6.17) было линейной комбинацией уранений (6.16) или , что то же самое , чтобы вектор

 b==(b₁,…,b_n) (6.18)

был линейной комбинацией векторов

a_i ==(a_i1,…,a_in) i=1,2,…,m (6.19)

необходимо и достаточно , чтобы каждое решение системы (6.16) являлось решением уравнения (6.17).

Доказательство леммы . Пусть ранг матрицы (a_ij) коэффициентов системы (6.16) равен m₀ . Очевидно , что m₀<m . Если m₀<m, то уравнений системы (6.16) являются линейными комбинациями остальных. Отбросив те m-m₀ линейных уравнений , которые являются линейными комбинациями оставшихся , получили систему из m₀ линейно независимых уравнений . равносильную системе (6.16), причем уравнение (6.17) является линейной комбинацией уравнений системы (6.16) тогда и только тогда , когда оно является линейной комбинацией указанной системы из оставшихся m₀ уравнений. Поэтому будем с самого начала считать , что , m₀=m т.е. что ранг матрицы (a_ij) коэффициентов системы (6.16) равен m– числу уравнений этой системы.

Пусть система (6.16) и (6.16)-(6.17) равносильны. Это означает, что пространства их решений совпадают.Поскольку все уравнения основной системы (6.16) входят в расширенную систему (6.16)-(6.17), то каждое решение расширенной системы является и решением основной системы , т.е. пространство решений расширенной системы содержится в пространстве решений основной системы. Следовательно , слвпадение этих пространств равносильно равенству их размерностей.

Размерность s пространства решений системы линейных днородных уравнений равны , как известно , числу неизвестных n этой системы , из которого вычтем ранг r матрицы коэффициентов системы : s=n-r.Отсюда следует , что равносильность систем (6.16) и (6.16)-(6.17) означает равенство рангов их матриц.Ранг матрицы коэффициентов системы (6.16) по условию равен m , т.е. векторы (6.19) линейно независимы.

Ранг матрицы коэффициентов расширенной системы (6.16)-(6.17) согласно сказанному в наших условиях также равен m.Поэтому векторы (см.(6.18) и (6.19))

b, a₁,…, a_m (6.20)

линейно зависимы.А это означает , что b является линейной комбинацией векторов a₁,…, a_m.

В самом деле , линейная зависимость векторов (6.20) означает , что существуют такие числа _{0, 1},…,  _m, не все равные нулю . что

₀b+ ₁a₁+…+ _ma_m=0 (6.21)

Здесь заведамо ₀=0, так как в противном случае векторы a₁,…, a_m оказались бы линейно зависимыми. Поделив равенство (6.21) на ₀, получим , что b является линейной комбинацией векторов a₁,…, a_m .

Обратно, если b является линейной комбинацией векторов (6.19), то в системах векторов (6.19) и (6.20) имеется в точности по m линейно независимых векторов , т.е. ранги матриц коэффициентов систем уравнений (6.16) и (6.16)-(6.17) равны.

Итак, условие , что вектор b является линейной комбинацией векторов (6.19) :

₁a₁+…+ _ma_m=b

эквивалентно равенству рангов матриц коэффициентов рассматриваемых основной и расширенной системв уравнений, следовательно, эквивалентно их равносильности.

 ч.т.д.

Доказательство следствия сразу следует из леммы, поскольку системы (6.16) и (6.16)-(6.17) очевидно равносильны тогда и только тогда , когда каждое решение системы (6.16) является и решением уравнения (6.17) – остальные уравнения систем просто совпадают.

ч.т.д.

Замечание 1 : доказанная лемма и ее следствие имеют простую геометрическую интерпритацию в n–мерном евклидовом векторном пространстве Rⁿ, т.е. в n–мерном пространстве со скалярным произведением.Используя обозначение скалярного произведения, систему (6.16) можно записать в виде

(a_i,x)=0 i=1,2,…,m (6.22)

а уравнение (6.17) в виде

(b,x)=0 (6.23)

где векторы a₁,…, a_m и определены в (6.18) и (6.19) , а x=(x₁,x₂,…,x_m+1)

Множество всевозможных линейных комбинаций векторов a₁,…, a_m образуют подпространство пространства Rⁿ и называется подпространством, натянутым на эти векторы.Обозначим его через Z=( a₁,…, a_m).

Множество решений системы (6.22) состоит из всех векторов х, ортоганальных подпространству Z=( a₁,…, a_m) Обозначим это множество решений через Т.Оно также является подпространством пространства Rⁿ.

Подпространства L==Z(a₁,…, a_m) и Т называются ортоганальными дополнениями друг друга в пространстве Rⁿ.

Поскольку L=Z( a₁,…, a_m), то представимость вектора b в виде линейной комбинации векторов a₁,…, a_m равносильна его принадлежности подпространству L пространства Rⁿ:b L.Это условие в свою очередь, равносильно ортоганальности вектора b подпространству Т:b _Т, которая означает, что для всех x Т имеет место равенство (b,x)=0,т.е.что любое реение х системы (6.22) является решением уравнения (6.23).Это и является утверждением следствия леммы.

Замечание 2 : напомним метод, которым можно получить все решения однородной системы линейных уравнений.Пусть система (6.16) состоит из линейно независимых уравнений.Тогда ранг матрицы его коэффициентов равен m.Это означает , что существует минор этой матрицы порядка m, не равный нулю.Пусть для определенности

a₁₁… a_1m

a_m1… a_mm (6.24)

В этом случае все решения системы (6.16) можно получить , задавая произвольно последние n-m координаты вектора (x₁,x₂,…,x_n). Остальные координаты однозначно находятся из системы уравнений (6.16).В самом деле, возьмем произвольное решение (x₁⁽⁰⁾,x₂⁽⁰⁾,…,x_n⁽⁰⁾) системы (6.16).После подстановки x_m+1= x⁽⁰⁾ _m+1,…, x_n= x_n⁽⁰⁾ в (6.16) получится система из m линейных уравнений (с m неизвестными x₁,x₂,…,x_n), матрицы коэффициентов которой в силу условия (6.24) невырожденная.Поэтому существуют единственные значения x₁,x₂,…,x_n, удовлетворяющие получившейся системе.Поскольку (x⁽⁰⁾₁,x⁽⁰⁾₂,…,x⁽⁰⁾_n). также было решением системы (6.16), то x₁=x⁽⁰⁾₁, x₂=x⁽⁰⁾₂,…, x_m=x⁽⁰⁾_m .

Перейдем теперь к анализу стационарных точек функции Лагранжа.

Теорема 6.2: Пусть функции f₀, f₁, f₂,…, f_m непрерывно дифференцируема в области G Rⁿ, x⁽⁰⁾ G

f_i(x)=0, i=1,2,3,…,n

 а ранг матрицы Якоби функций f₁, f₂,…, f_m в точке x⁽⁰⁾ равен m.Для того чтобы в точке x⁽⁰⁾=(x⁽⁰⁾₁,x⁽⁰⁾₂,…,x⁽⁰⁾_n) градиент f₀ являлся линейной комбинацией градиентов f₁, f₂,…, f_m необходимо и достаточно, чтобы точка x⁽⁰⁾=(x⁽⁰⁾₁,x⁽⁰⁾₂,…,x⁽⁰⁾_n) была стационарной точкой для функции.

g(x)=g(x_m+1,…,x_n)

Напомним,что если в точке x⁽⁰⁾ градиент f₀ является линейной комбинацией

f₀= ₁f₁+ ₂f₂+…+ _mf_m (6.25)

градиентов f₁, f₂,…, f_m, то это равносильно тому, что существует функция Лагранжа

F= f₀- ₁f₁- ₂f₂-…- _mf_m (6.26)

для которой точка x⁽⁰⁾ является стационарной :

 F(x⁽⁰⁾)

x_i i=1,2,…,n (6.27)

Это просто координатная запись (6.25) ,ибо в силу (6.26)

F(x⁽⁰⁾) f₀ f₁ f₂ f_m

x_i x_i x_i x_i x_i i=1,2,…,m

Доказательство: По условию ранг матрицы Якоби системы функций f₁, f₂,…, f_m в точке x⁽⁰⁾ равен m .Будем считать для определенности , как и в пункте 6.2 ,что

(f₁, f₂,…, f_m)

 (x₁,x₂,…,x_m) x⁽⁰⁾ (6.28)

Подставим в уравнение связи (6.3) функции (6.5) , являющиеся решением этих уравнений , и продеффиренцируем получившееся относительно переменных x_m+1,…,x_n тождества.Получим для точки x⁽⁰⁾ равенства df_i(x⁽⁰⁾)=0, i=1,2,…,m,  справедливые для любых приращений dx_m+1,…,dx_n независимых переменных x_m+1,…,x_n (напомним, что дифференциал являетсся линейной функцией , определенной на всем пространстве)Использовав инвариантность формы первого дифференциала относительно выбора переменных , получим , что в точке выполняется равенство

f_i f_i f_i f_i i=1,2,…,m

x₁ x_m x_m+1 x_n (6.29)

где x_m+1,…,x_n произвольные , а x₁,…,x_m находятся изформул (6.5). Таким образом вектор dx=( dx₁,…,dx_m,dx_m+1,…,dx_n) является решением линейной однородной системы (6.29).

Отметим , что в силу условия (6.28) значения dx₁,…,dx_m при заданных dx_m+1,…,dx_n однозначно находятся и из системы (6.29). Из замечания 2 следует также , что указанным способом получаются все решения системы (6.29).

Стационарность точки x⁽⁰⁾ для функции g(x)=g(x_m+1,…,x_n)

 означает , что dg(x⁽⁰⁾).Это равенство , в силу инвариантности формы первого дифференциала, можно более подробно записать в виде

f₀ f₀ f₀ f₀

x₁ x_m x_m+1 x_n (6.31)

 где dx_m+1,…,dx_n можно задавать произвольно, а dx₁,…,dx_m следует находить из формул (6.5) или , что дает тотже результат из формул (6.29). Инач говоря , любое решение системы уравнений (6.29) является и решением уравнения (6.31). Согласно следствию из леммы это возможно тогда и тoлько тогда , когда уравнение (6.31) является линейной комбинацией уравнений системы (6.29) , т.е. когда существуют такие числа , что

f₀= ₁f₁+ ₂f₂+…+ _mf_m

ч.т.д.

 Замечание 3 : Согласно замечанию 2 совокупность всех решений систеиы уравнений (6.29) образуют подпространство Т пространства Rⁿ, являющееся ортогональным дополнением к подпространству L=Z( f₁, f₂,…, f_m) . Любой вектор y T ортогонален каждому градиенту f_i , а поэтому его естественно назвать касательным вектором в точке x⁽⁰⁾ к гиперповерхности f_i(x)=0 , являющиеся множеством уровня функций f_i,i=1,2,…,m.

Таким образом , пространство решений Т системы (6.29) состоит из векторов , касательных одновременно ко всем гиперповерхностям f_i(x)=0 ,i=1,2,…,m, и потому его называют касательным пространством персечений всех гиперповерхностей f_i(x)=0 ,i=1,2,…,m . Напомним , что векторы касательноо пространства Т ,т.е. решения системы (6.29), были обознаены через dx (см.(6.30)).

Поскольку в точке условного экстремума согласно теореме 2 имеет место включение

f₀ L=Z( f₁, f₂,…, f_m)

то

f₀ T

 Иначе говоря, градиент f₀ одновременно ортогонален всем касательным dx к гиперповерхностям f_i(x)=0 ,i=1,2,…,m:

( f₀,dx)=0

 (это другая запись уравнения (6.31)), т.е. градиент f₀ перпендикулярен касательному пространству Т в точке x⁽⁰⁾ .Но множество всех векторов , ортогональных к f₀, образуют (n-1)– мерное пространство Т₀ , называемое касательным пространством к гиперповерхности f₀(x)= f₀(x⁽⁰⁾) .В силу сказанного выше , каждый вектор из Т , будучи ортогонален градиенту f₀, принадлежит к Т₀ , т.е. Т Т₀.

Итак , если x⁽⁰⁾ – точка условного экстремума , то . Т Т₀ , т.е. касательное пространство в точке x⁽⁰⁾ пересечения всех гиперповерхностей , задаваемых уравнениями связи , содержится в касательном пространстве в той же точке гиперповерхности.

Замечание 4 : Из теоремы 2 еще раз вытекает следствие теоремы 1.В самом деле , если x⁽⁰⁾ является точкой условногo экстремума , то является x⁽⁰⁾ точкой обычного экстремума для функции () и , следовательно , ее стационаоной точкой . Поэтому согласно теореме 2 точка x⁽⁰⁾ является стационарной точкой для функции Лагранжа , т.е.выполняется условие .

6.5.Достаточные условия для точек условного экстремума.

В этом пункте также будем предполагать выполненными все предположения , наложенные на функции в пункте 6.2.Пусть

F= f₀+ _if_i

-функции Лагранжа (см.(6.11)) для функции f₀ и уравнений связи(6.3).Пусть x⁽⁰⁾ G удовлетворяет уравнениям связи (6.3) и является стационарной точкой функции Лагаранжа , т.е. точкой , координаты которой удовлетворяют системе уравнений (6.10) и (6.3). Нашей целью является получение метода , с помощью которого можно установить условия , достаточные для того , чтобы x⁽⁰⁾ являлась точкой условного экстремума рассматриваемой задачи.

Заметим прежде всего , что если точка x G удовлетворяет уравнениям связи (6.3) , то

f= f(x)-f(x⁽⁰⁾)=F(x)-F(x⁽⁰⁾)= F (6.32)

Отсюда сразу видно , что если x⁽⁰⁾ является точкой обычного экстремума для функции F, т.е. F не меняет знака в некоторой окрестности точки x⁽⁰⁾, то x⁽⁰⁾ является точкой условного экстремума для функции f₀ .

Действительно , из (6.32) следует в этом случае , что приращение f₀ для допустимых значений х , т.е. удовлетворяющих уравнениям связи , также не меняет знак, Это достаточное условие , однако , накладывает слишком сильное ограничение на поведение функции Лагранжа F(x) в рассматриваемой точке – она должна иметь обычный экстремум , что сильно сужает область возможного применения указанного условия при решении задач.Поэтому целесообразно получить более общий достаточный признак условного экстремума .

Пусть x⁽⁰⁾= (x⁽⁰⁾₁,x⁽⁰⁾₂,…,x⁽⁰⁾_n) удовлетворяет уравнениям связи (6.3).Вернемся к рассмотрению функции (6.6) , т.е. функции g(x)=g(x_m+1,…,x_n) , получаемой из f₀(x)= f₀(x₁,x₂,…,x_n) при условии , что являются x₁,x₂,…,x_m функциями переменных x_m+1,…,x_n определяемых уравнениями связи (6.3) в некоторой окрестности точки x⁽⁰⁾.Будем дополнительно предполагать , что f₀(x ) и f_i(x ) ,i=1,2,…,m дважды непрерывно дифференцируема в точке x⁽⁰⁾.

Выше отмечалось (в пункте 6.2) , что x⁽⁰⁾ является точкой условного (строгого) экстремума для функции f₀(x) относительно уравнений связи (6.3) тогда и только тогда , когда x⁽⁰⁾ является точкой обычного (строгого) экстремума для функции g(x).Поэтому , если например , в точке x⁽⁰⁾ функция g(x) удовлетворяет достаточным условиям существования строгого экстремума,то в этой точке функция f₀(x) имеет условный строгий экстремум относительно уравнений связи (6.3).Достаточные условия для обычного сторого экстремума были получены нами ранее .Для нашего случая они имееют вид :

1)     g(x⁽⁰⁾ )

x_i i=m+1,…,n; (6.33)

2)второй дифферециал

²g(x⁽⁰⁾ )

d²g(x⁽⁰⁾ )= -----------dx_idx_j (6.34)

x_i x_j

является положительно или отрицательно определенной квадратичной формой.

При выполнении этих условий x⁽⁰⁾ является точкой строгого минимума или максимума для функции g(x).В силу сказанного выше указанные условия являются и достаточными условиями для того, чтобы x⁽⁰⁾ являлось точкой условного строго минимума (максимума) для функции f₀(x) относительно уравнений связи (6.3). Однако они неудобны для практического использования , так как требуют знания функции g(x).Поэтому , исходя из полученных достаточных условий условного строгого экстремума , выраженных посредством функции g(x) , получим достаточные условия того же экстремума , но выраженные только через функцию Лагранжа и уоавнений связи.

Прежде всего заметим , что в силу условия (6.4) система (6.29) разрешима, и притом однозначно, относительно dx₁,…,dx_m при произвольно фиксированных dx_m+1,…,dx_n .Систему (6.29), выражающую равенство нулю дифференциалов функции f_i(x) в точке x⁽⁰⁾:

d f_i(x)=0, i=1,2,…,m

при выполнении условий (6.3) , будем записывать кратко в виде :

df=0 (6.35)

где

f=(f₁,f₂,…,f_m)

Пусть x⁽⁰⁾ является стационарной точкой для функции Лагранжа F(x).Это означает, что dF(x⁽⁰⁾)=0, т.е. что в этой точке f₀+ _if_i=0.В теореме 2 показано, что в том случае x⁽⁰⁾ является стационарной точкой для функции, т.е.

 dg(x⁽⁰⁾)=0 (6.36)

Поясним еще раз вывод этой формулы и покажем, что

d²g(x⁽⁰⁾ )= d²F(x⁽⁰⁾ ) _df=0 (6.37)

Это равенство следует понимать как равенство функции n-m переменных dx_m+1,…,dx_n.В правой части равенства (6.37) остальные переменные dx₁,…,dx_m, которые входят в выражения написанных дифференциалов, определяются из системы уравнений (6.35) или, что равносильно (см. формулы (6.5))

dx_k=d _k(x₁,x₂,…,x_n-m), k=1,2,…,m

Используя инвариантность формы первого дифференциала относительно выбора переменных и формулу (6.6), имеем

f₀ (x⁽⁰⁾ )

dg(x⁽⁰⁾ )= -----------dx_j

x_j

Прибавим к этому равенству сумму (равную нулю) левых частей тождеств (6.29), умноженных соответственно на постоянные _i, входящие в функцию Лагранжа F(x) (точнее, i-е равенство (6.29) умножается на постоянную _i).Тогда, использовав условие (6.11), получим

F(x⁽⁰⁾)

dg(x⁽⁰⁾ )= -------[f₀ (x )+ _if_i (x)] dx_j = --------- dx_j=0

x_j  x=x₀ x_j

Утверждение (6.36) доказано.

Равенство (6.37) доказывается аналогичным приемом.Прежде всего напишем второй дифференциал для функции g(x) в точке x⁽⁰⁾:

²f₀(x⁽⁰⁾ )   f₀(x⁽⁰⁾ )

d²g(x⁽⁰⁾ )= -----------dx_jdx_k + ----------- d²x_j (6.38)

x_j x_k x_j

Далее продифференцировав тождества, получающиеся в результате дифференцирования уравнений связи (6.3), т.е. тождества будем иметь в точке x⁽⁰⁾ :

²f₀(x⁽⁰⁾ )   f₀(x⁽⁰⁾ )

d²g(x⁽⁰⁾ )= -----------dx_jdx_k + ----------- d²x_j =0 (6.39)

x_j x_k x_j

i=1,2,…,n

Умножив i–е равенство (6.39) на постоянную _i, входящую в функцию Лагранжа F(x), прибавим получившееся выражение к правой части равенства (6.38) ; тогда получим

²F(x⁽⁰⁾ )   F(x⁽⁰⁾ )

d²g(x⁽⁰⁾ )= -----------dx_jdx_k + ----------- d²x_j (6.38)

x_j x_k x_j

где dx_i, i=1,2,…,n удовлетворяет системе уравнений (6.35).Поскольку x⁽⁰⁾ точка стационарная для функции Лагранжа, то второй член получившегося равенства обращается в нуль, и тем самым формула (6.37) доказана.

Будем говорить, что квадратичная форма d²F(x⁽⁰⁾ ) является положительно (отрицательно) определенной квадратичной формой переменных dx_i, i=1,2,…,n, при условии, что эти переменные удовлетворяют системе уравнений (6.35), если для любых dx_i, i=1,2,…,n , удовлетворяющих этой системе уравнений и таких, что (dx_i)²>0 выполняется неравенство d²F(x⁽⁰⁾ ) >0 (соответственно d²F(x⁽⁰⁾ ) <0)

Пусть точка x⁽⁰⁾ удовлетворяет уравнениям связи (6.3) и является стационарной для функции Лагранжа (6.11) и пусть второй дифференциал функции Лагранжа в этой точке является положительно (отрицательно) определенной квадратичной формой переменных dx₁,…,dx_n, при условии, что они удовлетворяют системе уравнений (6.35).Тогда из (6.36) и (6.37) следует, что x⁽⁰⁾ является стационарной точкой для функции g(x) и что второй дифференциал этой функции в точке x⁽⁰⁾ является положительно (отрицательно) определенной квадратичной формой переменных dx_m+1,…,dx_n, и, следовательно, функция имеет в точке x⁽⁰⁾ строгий минимум (максимум) , а значит, функция f₀(x) имеет в точке x⁽⁰⁾ условный строгий минимум (максимум) относительно уравнений связи (6.3).

Сформулируем полученный результат в виде теоремы.

Теорема 6.3: Если x⁽⁰⁾ удовлетворяет уравнениям связи (6.3) и является стационарной точкой для функции Лагранжа (6.11) и если второй дифференциал функции Лагранжа в этой точке является положительно (отрицательно) определенной квадратичной формой переменных dx₁,…,dx_n при условии, что они удовлетворяют системе уравнений (6.29), то x⁽⁰⁾ является точкой строгого минимума (максимума) для функции f относительно уравнений связи (6.3).

Таким образом, чтобы исследовать стационарную точку функции Лагранжа (6.11) на условный экстремум, надо исследовать на определенность квадратичную форму (6.37), т.е. второй дифференциал функции Лагранжа в этой точке при выполнении условий связи (6.3) (когда дифференциалы dx_i, i=1,2,…,n связаны соотношениями (6.29)).При этом следует иметь в виду, что если второй дифференциал функции Лагранжа в рассматриваемой точке окажнтся положительно (отрицательно) определенным и без выполнения условий связи, то он будет и таковым , конечно, и при их выплнении.

.

7.Заключение.

Математический анализ это совершенно естественная, простая и элементарная наука, ничуть не более заумная, сложная или “высшая”, чем, скажем, “элементарная” геометрия. Многие теоремы, традиционно входившие в курс геометрии, куда сложнее, чем основополагающие теоремы классического анализа. Ныне противопоставление элементарной математики и анализа непродуктивно, и вовсе необязательно проявлять бездну остроумия только лишь из боязни использовать свойства производной.

Привнесение элементов математического анализа в школьные программы неизбежно приведет к перестройке и других областей математического образования – изменится содержание конкурсных задач, кружковой работы, математических олимпиад и многого другого. Теперь уже невозможно не учитывввать, что школьник должен знать нечто из ранее недоступной ему высшей математики.

При этом следует иметь в виду, что если освоены лишь самые основы математического анализа, можно уже делать попытки подобраться ко многим современным проблемам.

При рассмотрении данной темы дипломного проекта теоритические сведения подтвердились практическим доказательством и математическим обоснованием.

8. Библиография.

1.А.Ф.Бермант, И.Г.Араманович Краткий курс математического анализа.-М.: Наука, 1973.

2.И.Е.Жак Дифференциальное исчисление.-М.:Государственное учебно-педагогическое издательство министерства просвещения РСФСР, 1960.

3.Г.И.Запорожец Руководство к решению задач по математическому анализу.-М.: Высшая школа,1966.

4.В.А.Зорич Математический анализ.-М.: Наука, 1981.

5.А.П.Картышев, Б.Л.Рождественский Математический анализ.-М.: Наука, 1984.

6.А.Н.Колмогоров, С.В.Фомин Элементы теории функций и функционального анализа.-М.: Наука, 1981.

7.Л.Д.Кудрявцев Курс математического анализа.-М.: Высшая школа, 1981.

8.А.Г.Моркович, А.С.Солодовников Математический анализ.-М.: Высшая школа, 1990.

9.Н.С.Пискунов Дифференциальное и интегральное исчисление. т.1.-М.: Наука, 1978.

10.К.А.Рыбников История математики.-М.:Издательство Московского университета, 1994.

11.В.М.Тихомиров Рассказы о максимумах и минимумах.-М.:Наука, 1986.

12.Г.М.Фихтенгольц Основы математического анализа. т.2.-М.: Наука, 1968.

13.Г.М.Фихтенгольц Курс дифференциального и интегрального исчисления. т.1.-М.: Наука, 1969.