Грассман с самого начала движим интересом к n-мерному пространству, чего совершенно нет у Гамильтона

2. Грассман с самого начала движим интересом к n-мерному пространству, чего совершенно нет у Гамильтона.

3. У Гамильтона по сравнению с Грассманом есть, однако, одно дополнительное понятие - понятие поля - делающее кватернионы важными с точки зрения физики.

Обе части кватерниона Гамильтон рассматривает как функции точки; он представляет себе, что к каждой точке пространства приложен кватернион, то есть скаляр и вектор. К такому полю кватернионов

t(x,y,z)+iu(x,y,z)+jv(x,y,z)+kw(x,y,z)

он применяет определенные операции, в результате чего возникают новые поля. Операции эти Гамильтон, следуя специальной, разработанной в Кембридже методике, изображает с помощью так называемых "символических обозначений". Скажем, теорему Тейлора в кембриджской школе принято было записывать в виде

где выражение полагалось мыслить расписанным по правилу разложения показательной функции в ряд, а входящие в него произведения 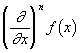означали частные производные .

Применяя этот способ и здесь, Гамильтон строит из частных производных по координатам точки поля так называемые символические "операторы". Важнейшим из них является оператор, обозначенный Гамильтоном знаком и названный им, вследствие сходства с одним древним музыкальным инструментом, "наблой":

Формально с этой наблой обращаются так, как если бы она была вектором. Будучи применена к полю кватернионов, она немедленно приводит к ряду важнейших понятий векторного анализа. Так, например, если t - скаляр, то

является вектором, "градиентом t", указывающим в каждой точке величину и направление наибольшего возрастания t.

Будучи применена к вектору iu+jv+kw, операция дает кватернион

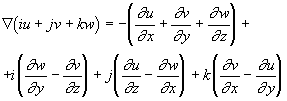
Скалярная часть этого кватерниона называется дивергенцией поля, а векторная - его вихрем.

Попытка разъяснить здесь то исключительное значение, которое понятия эти имеют для физики, завела бы нас слишком далеко. Я укажу лишь, что двукратное применение оператора к скаляру приводит к скаляру

играющему фундаментальную роль в теории потенциала.

Легкость и изящество, с которыми получаются здесь глубочайшие по своему содержанию теоремы, действительно поразительны. Этим и объясняется восхищение кватернионистов своей системой, восхищение, которое отвергало все остальное и, как уже отмечалось, вскоре вышло за пределы разумного настолько, что стало наносить ущерб не только математике в целом, но и самой теории кватернионов. Такому развитию событий способствовал и доведенный до совершенства, с благоговейным почитанием возделываемый формализм. Возникли большие надежды на дальнейшее планомерное развитие этой теории по привычным математическим образцам. К построенному на основе четырех арифметических действий исчислению кватернионов должна была примкнуть алгебра с подробно разработанной теорией уравнений вида P(x₁, x₂, ..., x_n)=0, где P(x₁, x₂, ..., x_n) - многочлен, зависящий от кватернионов x₁, x₂, ..., x_n. Конечной целью явилось - и остается поныне - построение теории функций кватернионов, от которой ждали совершенно новых, необычных по своему охвату открытий общематематического значения. Чтобы содействовать достижению этой цели, не очень определенной, но принятой с верой в нее, в 1895 г. был даже основан «Всемирный союз в поддержку кватернионов»! Независимо даже от того, что всегда более правильно скептически относиться к такого рода культивированию и насаждению какого-либо одного научного направления, теперь уже можно с определенностью утверждать, что предприятие это должно считаться потерпевшим крушение или, во всяком случае, бесплодным. Следование по набросанному выше пути - который претендовал на новизну, хотя фактически сводился к почти буквальному перенесению давно известных идей на один-единственный объект и, значит, вообще не содержал в себе никакой гениальной концепции - повело ко всякого рода обобщениям известных теорем, которые при такой общности теряли свою специфику и становились беспредметными. Только в отдельных случаях получились частные результаты, доставляющие известное удовлетворение. Так, например, оказалось, что в области кватернионов не имеет места основная теорема алгебры, зато каждый кватернион удовлетворяет некоторому кубическому уравнению.

Критика; матричное исчисление Кэли.

Однако, упрямо следуя намеченным путем, кватернионисты упустили из виду более глубокие проблемы, представлявшие для науки действительный интерес. Так, из-за своей предвзятости они не поняли того простого факта, что, кинув на сложившуюся ситуацию взгляд сверху, они приобрели бы отчетливое представление относительно границ области, где применение их теории является плодотворным, и что вместе с этими ораничениями они получили бы и четкие указания относительно ведущего к успеху пути.

Этим более глубоким осознанием создавшегося положения вещей мы обязаны Кэли. В своей работе «A Memoir on the Theory of Matrices» («Мемуар по теории матриц»; Philosophical Transactions, 1858) он развил некоторое матричное исчисление, имеющее дело с 4-, 9-, 16-, n²- членными комплексными числами и в качестве частного случая охватывающее также и кватернионы. Действия над матрицами отталкивалются у Кэли от очень простой идеи, состоящей в том, что с матрицами, возникающими в теории линейных подстановок, следует обращаться по правилам, инспирированным этой теорией. Соответственно этому сложение двух матриц должно осуществляться сложением соответствующих их элементов:

Умножение же матриц производится последовательным выполнением представляемых ими подстановок, то есть по хорошо известному правилу умножения определителей. В случае, когда n = 2,

Правило перемножения кватернионов содержится в этом правиле в качестве частного случая.

В самом деле, будем понимать под i обычный квадратный корень из -1 и положим

так что определитель окажется равным

Положим соответственно

и выполним умножение по указанному правилу, принимая во внимание, что i²=-1. Тогда получится некоторая новая матрица, имеющая вид

где четыре величины A, B, C и D имеют следующие значения:

A = dx + at + bz - cy

B = dy - az + bt + cx

C = dz + ay - bx + ct

D = dt - ax - by - cz

Таким образом, мы действительно по двум кватернионам d+ix+jy+kz и t+ix+jy+kz построили третий, который получается из них умножением по Гамильтону.

Результат этот, поначалу кажущийся неожиданным, при ближайшем рассмотрении оказывается абсолютно понятным, если исходить из геометрического существа рассматриваемой ситуации. Поскольку действия над кватернионами тем самым представляют собой не что иное, как оперирование с бинарными линейными подстановками, мы можем заключить, что для плодотворного применения кватернионов характерным является случай, когда в рассмотрении участвуют такого рода подстановки. Это объясняет, в частности, почему кватернионы так полезны в теории растяжений с вращением. Каждое растяжение с вращением оставляет неподвижной мнимую сферическую окружность, то есть геометрический образ, точки которого рационально выражаются через один-единственный параметр . Поэтому, если записать в однородном виде , то при растяжении пространства с одновременным его вращением параметры , подвергаются бинарной линейной подстановке.

Сходным образом объясняется и блеск, с которым кватернионы применяются в теории относительности. Здесь инвариантной оказывается поверхность второго порядка в R₄. Эта поверхность несет два семейства прямых, каждое из которых описывается одним параметром или . При растяжении с вращением каждый из этих параметров подвергается бинарной линейной подстановке.

Список литературы

Для подготовки данной работы были использованы материалы с сайта http://karataev.nm.ru/